SVM-支持向量机（一）线性SVM分类

SVM-支持向量机

SVM（Support Vector Machine）-支持向量机，是一个功能非常强大的机器学习模型，可以处理线性与非线性的分类、回归，甚至是异常检测。它也是机器学习中非常热门的算法之一，特别适用于复杂的分类问题，并且数据集为小型、或中型的数据集。

这章我们会解释SVM里的核心概念、原理以及如何使用。

 

线性SVM分类

我们首先介绍一下SVM里最基本的原理。这里先看一张图：

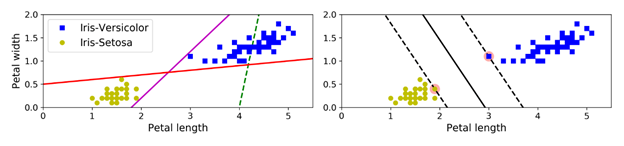
这个是Iris数据集中的部分数据，可以看到这两个类别可以由一条直线很简单地直接分开（也可以说它们是线性可分）。左边的图上画出了3个可能的线性分类器的决策边界，其中绿色的最差，因为它无法将两个类别区分开来。另外两个看起来在训练集上表现良好，但是它们的决策边界与数据离的太近，所以如果有新数据引入的话，模型可能不会在新数据集上表现良好。再看看右边的图，实线代表的是一个SVM分类器的决策边界。这条线不仅将两个类别区分了开来，同时它还与（离此决策边界）最近的训练数据条目离的足够远。大家可以把SVM分类器看成一个：在两个类别之间，能有多宽就有多宽的大马路（这大马路就是右图的两条平行虚线）。这个称为 large margin classification（大间距分类）。

可以看到的是，在数据集中新增加的训练数据在“马路外侧”的话，则不会对决策边界产生任何影响，决策边界完全仅由“马路线”（右图虚线）上的数据决定。这些决策边界上的数据实例称为支持向量（support vectors），如右图中的两个圆。

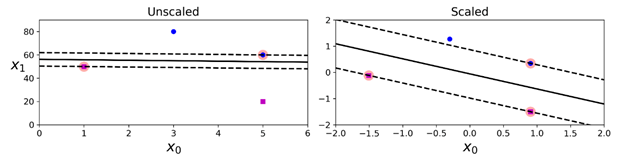
需要注意的是，SVM对特征的取值范围非常敏感，如下图所示：在左边的图中，纵坐标的取值范围要远大于横坐标的取值范围，所以“最宽的马路”非常接近水平线。在做了特征缩放（feature scaling）后，例如使用 sk-learn的StrandardScaler，决策边界便看起来正常的多了（如下右图）。

 

软间隔分类（Soft Margin Classification）

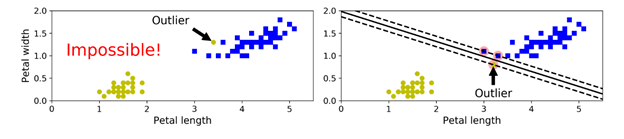
如果我们严格地要求所有点都不在街道上并且被正确的分类，则这个称为硬间隔分类（hard margin classification）。硬间隔分类中有两个主要问题，第一，这个仅在线性可分的情况下适用；第二，它对异常点非常敏感。如下图所示，在左边的图中，如果存在这种异常点，则无法找到一个硬间隔（hard margin）。在右边的图中，如果存在这种类型的异常点，则最终的决策边界与我们之前的决策边界会有很大的差异，并且它的泛化性能可能并不太好。

 

为了避免这些情况，我们需要用一个更灵活的模型。所以我们的目标是：在“保持街道足够宽”与限制“间隔侵犯”（margin violations，意思是说数据条目最终在街道中间，或者甚至是在错误的一边）之间找到一个良好的平衡。这个称为软间隔分类（soft margin classification）。

在sk-learn SVM 类中，我们可以通过c参数控制这个平衡。较小的c值会使得街道更宽，但是间隔侵犯（margin violation）会更多。下图是两个软间隔SVM分类器在同一个非线性可分的数据集上的决策边界与间隔：

 

在左边的图中，使用的是一个较小的c值，可以看到间隔非常大，但是很多实例都在街道上。在右边的图中，使用的是一个较大的c值，所以分类器作用后的间隔侵犯（margin violation）较少，但是间隔也比较小。不过从整体来看，第一个分类器的泛化性能看起来会更好（在训练集上的预测仅有少部分预测错误，因为虽然有margin violation，但是实际上大部分的margin violation还是在它们所属的决策边界那边）。

这里需要提示大家的是：如果SVM出现了过拟合，则可以尝试通过降低c的值来进行正则化。

下面是一个示例代码，加载iris 数据集，对特征进行缩放，然后训练一个线性SVM模型（使用LinearSVC 类，指定C=1以及hinge 损失函数）用于检测Iris-Virginica flowers。模型的结果就是上图中C=1时的图：

import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

iris = datasets.load_iris()
X = iris['data'][:, (2,3)] # petal length, petal width
y = (iris['target'] == 2).astype(np.float64) # Iris-Virginica

svm_clf = Pipeline([
    ("scaler", StandardScaler()),
    ("linear_svc", LinearSVC(C=1, loss="hinge")),
])

svm_clf.fit(X, y)

 

然后使用训练好的模型做预测：

svm_clf.predict([[5.5, 1.7]])
>array([1.])

 

上面的代码也可以进行改写，也可以用SVC类，使用SVC(kernel="linear", C=1)。但是它的速度会慢很多，特别是训练集非常大时，所以并不推荐这种用法。另外的一种用法是使用SGDClassifier类，SGDClassifier(loss="hinge", alpha=1/(m*C))。这样会使用随机梯度下降训练一个线性SVM分类器。它的收敛不如LinearSVC类快，但是在处理非常大的数据集时（无法全部放入内存的规模）非常适用，或者是处理在线分类任务（online classification）时也比较适用。

LinearSVC类会对偏置项（bias term）正则，所以我们应该先通过减去训练集的平均数，让训练集集居中。如果使用了StandardScaler处理数据，则这个会自动完成。另一方面，必须要确保设置loss的超参数为hinge，因为它不是默认的值。最后，为了性能更好，我们应该设置dual超参数为False，除非数据集中的特征数比训练数据条目还要多。