机器学习项目流程(二)探索并可视化数据
探索并可视化数据
到目前为止我们已经大致浏览了数据集,我们下一步的目标是更深入的了解数据集。
首先,我们要将测试集放在一边,确保我们仅浏览训练集。当然,如果训练集特别大的话,我们可能需要对它进行采样,获取它的一个小样本集进行研究。在我们的这个例子中,这个数据集非常小,所以我们可以直接在整个训练集上进行操作。我们先复制一份数据进行操作,以免干扰到原数据集:
housing = strat_train_set.copy()
可视化数据集
因为数据集中包含地理信息(经度与维度),所以我们可以基于此创建一个散点图,将数据可视化:
housing.plot(kind='scatter', x='longitude', y='latitude')
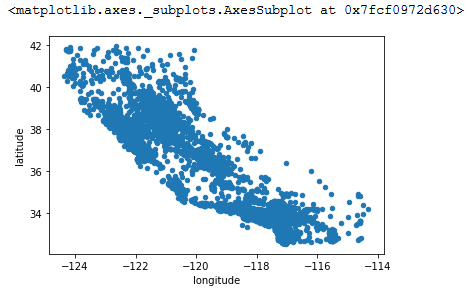
我们可以看到可视化出来的图像基本就是加州的地图样子,但是除此之外就基本看不到其他明显的特征了。在执行plot中可以指定alpha的值为0.1,可以让数据点密集的地方更突出:
housing.plot(kind='scatter', x='longitude', y='latitude', alpha='0.1')
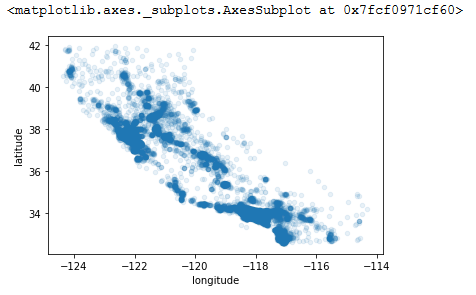
现在好多了,我们可以看到高密度的区域是哪几个区域,如果对加州有一定了解的人,应该可以分辨出这些是加州的哪些区域。
下面我们看一下房价的可视化图:
housing.plot(kind='scatter', x='longitude', y='latitude', alpha=0.4,
s=housing['population']/100, label='population', figsize=(10,7),
c='median_house_value', cmap=plt.get_cmap("jet"), colorbar=True)
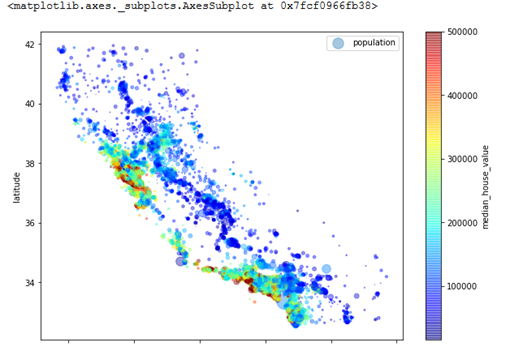
这里圆点的直径越大说明人口密度越大(由 s 的选项指定),颜色代表房价(由 c 的选项指定)。同时我们也使用了一个预定义的jet颜色图(由cmap选项指定),通过颜色区分房价的高低。
从这个图中,我们可以明显感知到房价与地理位置(例如靠海的地方价格高)以及人口密度的关系十分紧密。我们接下来可以尝试用一个聚类算法检测出几个主要的簇(clusters),并且为数据集增加一个属性,用于衡量每条数据到各个簇中心的距离。这个可能会对预测由帮助。另一方面,靠海的距离乍一看可能也可以作为一个有用的属性,但是最北边的地方虽然也靠海,但是房价也并不是特别高,所以“靠海距离”这个规则可能并不是特别简单有效。
寻找相关性
由于这个数据集并不大,所以我们可以很容易地算出每对(pair)属性的标准相关系数(standard correlation coefficient,也称为 Pearson’s r),方法为corr():
corr_matrix = housing.corr()
现在我们看一下每个属性与 median_house_value 的相关性:
corr_matrix['median_house_value'].sort_values(ascending=False)
median_house_value 1.000000
median_income 0.687160
total_rooms 0.135097
housing_median_age 0.114110
households 0.064506
total_bedrooms 0.047689
population -0.026920
longitude -0.047432
latitude -0.142724
Name: median_house_value, dtype: float64
相关系数的取值范围为-1到1,当接近1时,代表它们由很强的正相关性;例如:在median_income 上升时,房价也会倾向于上升。当相关系数接近于 -1 时,代表它们有很强的负相关性;我们可以看到latitude与median_house_value 之间存在一个较小的负相关性(也就是说,如果地理位置向北的话,房价会稍微下降)。最后相关性趋近于0,代表它们之间没有线性相关性。
这里需要注意的是:相关系数仅仅是衡量了线性相关(如果 x 上升,则y同样上升或是下降)。它可能会完全缺失非线性关系的衡量(例如,如果x 靠近0 时,y 上升)。
另一个检查属性间相关性的方法是使用Pandas的scatter_matrix() 方法,它会画出每对数值型属性之间的相关性。在这个数据集中,我们有9个数值型属性,会产生81 个图。我们可以先主要关注那些看起来与房价有相关性的属性:
from pandas.plotting import scatter_matrix
attributes = ['median_house_value', 'median_income', 'total_rooms', 'housing_median_age']
scatter_matrix(housing[attributes], figsize=(12, 8))
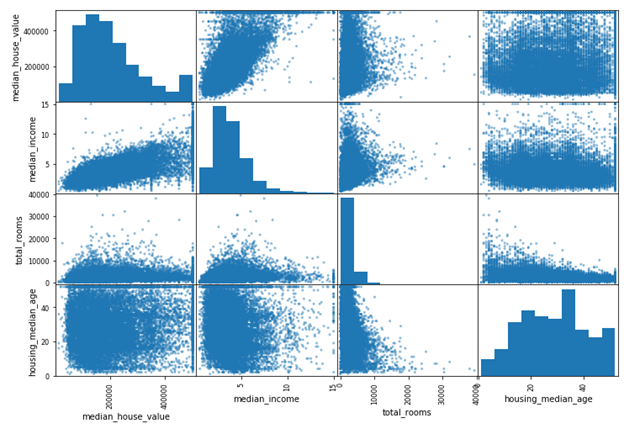
主对角线(左上到右下)是属性自身的相关性,如果画出来的话,就是一条直线,一般没什么用。所以Pandas 会默认画出此属性的直方图,而不是它们的相关性图(也可以修改它的参数,不使用默认的方式,这个可以去参考Pandas 官方文档)。
从上图我们可以看到,与median_house_value 正相关性最明显的是median_income 属性,所以我们放大它们的相关性散点图:
housing.plot(kind='scatter', x='median_income', y='median_house_value', alpha=0.1)
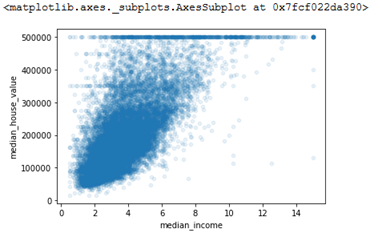
这个图告诉了我们几件事:
- 相关性确实非常强,我们可以清晰地看到上升的趋势,并且图中的点分布的也并不散
- 可以清晰地看到我们之前提到的价格上限($500,000),是一条明显的水平线。此图也揭示了其他稍微不太明显的水平线,例如大约$450,000的水平线、以及$350,000 附近的水平线,也可能存在 $280,000 的水平线(以及此价格以下的几条不太明显的水平线)。我们可能需要移除掉对应这些地区的点,防止模型学习并复现这些异常的数据。
尝试属性结合
前面我们提供了集中方法用于探索数据并gain insights。我们发现了部分异常数据,在将这些数据送入机器学习算法前,我们可能需要清楚这些异常数据。同时我们也探究了属性与目标label 之间的相关性。我们也注意到了一些属性存在长尾分布,所有我们可能要对它们进行转换(例如,计算它们的对数)。当然我们的目标是根据每个项目变动的,但是大体的方法是类似的。
在将数据送入机器学习算法前,最后一件要做的事是:尝试将多个属性进行结合。例如,在某条数据中,一个区域的total_rooms 的数目并不是特别有用,除非我们同时也知道在同一区域中有多少个家庭。更有意义的属性是每个家庭所拥有的房间数。类似,total_bedrooms 属性本身也并不是一个很有用的属性:我们可能更需要将它与其他房间数进行对比。另一个可能比较有用的属性是每个家庭的人口数。接下来我们创建这些新属性:
housing['rooms_per_household'] = housing['total_rooms']/housing['households']
housing['bedrooms_per_room'] = housing['total_bedrooms']/housing['total_rooms']
housing['population_per_household'] = housing['population']/housing['households']
然后我们再看一下相关性:
corr_matrix = housing.corr()
corr_matrix['median_house_value'].sort_values(ascending=False)

可以看到效果还不错,bedrooms_per_room 的属性相对于total_rooms 或是total_bedrooms 属性,与目标label 属性的相关性更大。显然,bedroom/room 比率更小的房子会更贵。rooms_per_household 也比total_rooms 对房价的相关性更大,显然房间更多的房子价格更贵。
这轮对数据的探究并不需要特别彻底,主要是方向正确即可,快速的获取更深的信息点可以帮助我们建立更合理、更好的原型。不过这个是一个迭代的过程:一旦我们建立了一个原型并开始运行,我们可以分析它的产出,去获取更深的insight,并且继续进行下一步探究。
这一节我们主要做的是:
- 可视化数据,做初步探究
- 了解数据相关性
- 组合属性,以获取与label 数据更相关的复合属性
下一步我们会为机器学习算法准备数据。



