树形背包浅谈
题目:选课
网址:https://www.luogu.com.cn/problem/P2014
描述
学校实行学分制。
每门的必修课都有固定的学分,同时还必须获得相应的选修课程学分。
学校开设了 \(N\) 门的选修课程,每个学生可选课程的数量 \(M\) 是给定的。
学生选修了这 \(M\) 门课并考核通过就能获得相应的学分。
在选修课程中,有些课程可以直接选修,有些课程需要一定的基础知识,必须在选了其他的一些课程的基础上才能选修。
例如《Windows程序设计》必须在选修了《Windows操作基础》之后才能选修。
我们称《Windows操作基础》是《Windows程序设计》的先修课。
每门课的直接先修课最多只有一门。
两门课可能存在相同的先修课。
你的任务是为自己确定一个选课方案,使得你能得到的学分最多,并且必须满足先修条件。
假定课程之间不存在时间上的冲突。
输入格式
输入文件的第一行包括两个整数\(N\)、\(M\)(中间用一个空格隔开)其中\(1≤N≤300,1≤M≤N\)。
接下来\(N\)行每行代表一门课,课号依次为\(1,2,…,N\)。
每行有两个数(用一个空格隔开),第一个数为这门课先修课的课号(若不存在先修课则该项为\(0\)),第二个数为这门课的学分。
学分是不超过\(10\)的正整数。
输出格式
输出一个整数,表示学分总数。
输入样例:
7 4
2 2
0 1
0 4
2 1
7 1
7 6
2 2
输出样例:
13
经典的背包问题。有依赖的背包问题。
将“0”作为整棵树的根节点。
定义状态:\(dp[u, j]\)指在结点\(u\)分配\(j\)个课程获得的学分最大值。
那么,怎么转移?
大体思路就是树分治的思想。因为我们仅会两个泛化物品的合并,而对于多个泛化物品,我们则显得尤为吃力。
这道题重点在于多个泛化物品合并操作。也就是树分治的思想。
那么,我们就一一进行合并,将合并成的新的物品在于其他泛化物品操作即可。
初始化的问题:对于题目没有强调恰好装满的情况下,所有的\(dp\)值均设为\(0\);如果题目要求“恰好装满”,则\(dp\)值均设为负无穷或\(-1\)(设为\(-1\)应特判),除了背包容量为\(0\)的\(dp\)值。
代码如下:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<cmath>
using namespace std;
const int maxn = 300 + 10;
int n, m, k[maxn], s[maxn];
vector <int> son[maxn];
int dp[maxn][maxn];
void dfs(int u)
{
for(int i = 0; i < son[u].size(); ++ i) dfs(son[u][i]);
for(int i = 1; i <= m + 1; ++ i) dp[u][i] = s[u];
for(int i = 0; i < son[u].size(); ++ i)
{
for(int j = m + 1; j; -- j)
{
int &ans = dp[u][j];
for(int k = 0; k < j; ++ k)
{
ans = max(ans, dp[son[u][i]][k] + dp[u][j - k]);
}
}
}
return;
}
int main()
{
memset(dp, 0, sizeof(dp));
for(int i = 0; i <= n; ++ i)
{
son[i].clear();
}
scanf("%d %d", &n, &m);
for(int i = 1; i <= n; ++ i)
{
scanf("%d %d", &k[i], &s[i]);
son[k[i]].push_back(i);
}
dfs(0);
printf("%d\n", dp[0][m + 1]);
return 0;
}
题目:有线电视网
网址:https://www.luogu.com.cn/problem/P1273
题目描述
某收费有线电视网计划转播一场重要的足球比赛。他们的转播网和用户终端构成一棵树状结构,这棵树的根结点位于足球比赛的现场,树叶为各个用户终端,其他中转站为该树的内部节点。
从转播站到转播站以及从转播站到所有用户终端的信号传输费用都是已知的,一场转播的总费用等于传输信号的费用总和。
现在每个用户都准备了一笔费用想观看这场精彩的足球比赛,有线电视网有权决定给哪些用户提供信号而不给哪些用户提供信号。
写一个程序找出一个方案使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。
输入格式
输入文件的第一行包含两个用空格隔开的整数\(N\)和\(M\),其中\(2≤N≤3000,1≤M≤N-1\),\(N\)为整个有线电视网的结点总数,\(M\)为用户终端的数量。
第一个转播站即树的根结点编号为\(1\),其他的转播站编号为\(2\)到\(N-M\),用户终端编号为\(N-M+1\)到\(N\)。
接下来的\(N-M\)行每行表示—个转播站的数据,第\(i+1\)行表示第\(i\)个转播站的数据,其格式如下:
\(K A1 C1 A2 C2 … Ak Ck\)
\(K\)表示该转播站下接\(K\)个结点(转播站或用户),每个结点对应一对整数\(A\)与\(C\),\(A\)表示结点编号,\(C\)表示从当前转播站传输信号到结点A的费用。最后一行依次表示所有用户为观看比赛而准备支付的钱数。
输出格式
输出文件仅一行,包含一个整数,表示上述问题所要求的最大用户数。
输入输出样例
输入
5 3
2 2 2 5 3
2 3 2 4 3
3 4 2
输出
2
说明/提示
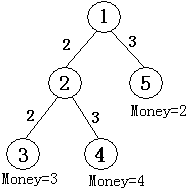
如图所示,共有五个结点。结点①为根结点,即现场直播站,②为一个中转站,③④⑤为用户端,共\(M\)个,编号从\(N-M+1\)到\(N\),他们为观看比赛分别准备的钱数为\(3、4、2\),从结点①可以传送信号到结点②,费用为\(2\),也可以传送信号到结点⑤,费用为\(3\)(第二行数据所示),从结点②可以传输信号到结点③,费用为\(2\)。也可传输信号到结点④,费用为\(3\)(第三行数据所示),如果要让所有用户(③④⑤)都能看上比赛,则信号传输的总费用为:
\(2+3+2+3=10\),大于用户愿意支付的总费用\(3+4+2=9\),有线电视网就亏本了,而只让③④两个用户看比赛就不亏本了。
这道题就有意思多了。首先,由于你不知道手上共有多少钱(也就是说你现在的钱为负数不代表今后的付款中也为负数),所以,将钱数作为背包的“容积”是不甚合理的。那么,可以转化一下:给有线电视网分配用户,要求满足一定数量的用户所赚的钱最大是多少。
由于最终问的是在不亏本的情况下,满足最多的用户。所以,最终利润仅需大于\(0\)即可。
这道题试想一下:如果你只有一个人,这时候你要分配\(2\)个用户给这名用户,如果初始化均为\(0\),那么整个答案是错误的。因而,我们必须将除了体积为\(0\)的\(dp\)值赋为\(0\)以外,其它赋为负无穷或\(-1\)即可。(因为你是要恰好分配的人数,如果名额多的话是不合理)
代码如下:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<cmath>
using namespace std;
const int maxn = 3000 + 10;
vector <int> son[maxn], cost[maxn];
int n, m, dp[maxn][maxn], s[maxn] = {};
void dfs(int u)
{
for(int i = 0; i < son[u].size(); ++ i)
{
dfs(son[u][i]);
s[u] += s[son[u][i]];
}
dp[u][0] = 0;
for(int i = 0; i < son[u].size(); ++ i)
{
for(int j = s[u]; j; -- j)
{
int &ans = dp[u][j], v = son[u][i], c = cost[u][i];
for(int k = 1; k <= j; ++ k)
{
ans = max(ans, dp[v][k] + dp[u][j - k] - c);
}
}
}
return;
}
int main()
{
scanf("%d %d", &n, &m);
for(int i = 1; i <= n; ++ i)
son[i].clear(), cost[i].clear();
for(int i = 1; i <= n - m; ++ i)
{
int k, A, C;
scanf("%d", &k);
for(int j = 1; j <= k; ++ j)
{
scanf("%d %d", &A, &C);
son[i].push_back(A), cost[i].push_back(C);
}
}
memset(dp, 0xcf, sizeof(dp));
for(int i = n - m + 1; i <= n; ++ i)
{
int t;
scanf("%d", &t);
dp[i][0] = 0, dp[i][1] = t;
s[i] = 1;
}
dfs(1);
for(int i = m; i >= 0; -- i)
{
if(dp[1][i] >= 0)
{
printf("%d\n", i);
break;
}
}
return 0;
}
习题:Bribing FIPA
网址:https://www.acwing.com/problem/content/326/
FIPA(国际国际计划协会联合会)近期将进行投票,以确定下一届IPWC(国际规划世界杯)的主办方。
钻石大陆的代表本内特希望通过以赠送钻石买通国家的方式,获得更多的投票。
当然,他并不需要买通所有的国家,因为小国家会跟随着他们附庸的大国进行投票。
换句话说,只要买通了一个大国,就等于获得了它和它统治下所有小国的投票。
例如,\(C\)在\(B\)的统治下,\(B\)在\(A\)的统治下,那么买通\(A\)就等于获得了三国的投票。
请注意,一个国家最多附庸于一个国家的统治下,附庸关系也不会构成环。
请你编写一个程序,帮助本内特求出在至少获得\(m\)个国家支持的情况下的最少花费是多少。
输入格式
输入包含多组测试数据。
第一行包含两个整数\(n\)和\(m\),其中\(n\)表示参与投票的国家的总数,\(m\)表示获得的票数。
接下来\(n\)行,每行包含一个国家的信息,形式如下:
\(CountryName\) \(DiamondCount\) \(DCName\) \(DCName\) …
其中\(CountryName\)是一个长度不超过\(100\)的字符串,表示这个国家的名字,\(DiamondCount\)是一个整数,表示买通该国家需要的钻石数,\(DCName\)是一个字符串,表示直接附庸于该国家的一个国家的名字。
一个国家可能没有任何附庸国家。
当读入一行为#时,表示输入终止。
输出格式
每组数据输出一个结果,每个结果占一行。
数据范围
\(1≤n≤200, 0≤ m≤n\)
输入样例:
3 2
Aland 10
Boland 20 Aland
Coland 15
#
输出样例:
20
这道题就是输入难。
其他的思路如出一辙。
代码如下:
#include<iostream>
#include<cstring>
#include<sstream>
#include<string>
#include<vector>
#include<cstdio>
#include<bitset>
#include<cmath>
#include<map>
using namespace std;
const int SIZE = 200 + 7, INF = 1 << 30;
vector <int> son[SIZE];
map <string, int> p;
bitset <SIZE> vis;
int n, m, tot, cost[SIZE], dp[SIZE][SIZE], size[SIZE], root;
void init()
{
tot = 0, p.clear(), vis.set();
memset(dp, 0x3f, sizeof(dp));
memset(size, 0, sizeof(size));
return;
}
void dfs(int u)
{
size[u] = 1;
for(int i = 0; i < son[u].size(); ++ i)
{
dfs(son[u][i]);
size[u] += size[son[u][i]];
}
dp[u][0] = 0;
for(int i = 1; i <= size[u]; ++ i) dp[u][i] = cost[u];
for(int i = 0; i < son[u].size(); ++ i)
{
int v = son[u][i];
for(int j = size[u] - 1; j; -- j)
{
int &ans = dp[u][j];
for(int k = j; k; -- k)
{
ans = min(ans, dp[v][k] + dp[u][j - k]);
}
}
}
return;
}
int main()
{
string s, line;
while(getline(cin, line))
{
if(line == "#") return 0;
stringstream ss(line);
ss >> n >> m;
init();
int u, v;
cost[0] = INF, son[0].clear();
for(int i = 1; i <= n; ++ i)
{
getline(cin, line);
stringstream ss(line);
ss >> s;
if(p.find(s) == p.end()) p[s] = ++ tot;
u = p[s];
ss >> cost[u];
son[u].clear();
while(ss >> s)
{
if(p.find(s) == p.end()) p[s] = ++ tot;
v = p[s];
vis[v] = 0;
son[u].push_back(v);
}
}
for(int i = 1; i <= n; ++ i)
{
if(!vis[i]) continue;
son[0].push_back(i);
}
dfs(0);
printf("%d\n", dp[0][m]);
}
return 0;
}
由此,我们大致可以发现这类问题的规律:
- 首先,这类问题问法都很类似,都是背包的基础上,把它“扔”在了树上:有依赖的背包。而往往dp方程有两维即可。
- 对于这样一种有依赖的背包,我们通常是通过不断合并两个泛化物品进行求解。也就是这样说,对于多个泛化物品的背包问题时,我们应当两两合并为一个大的泛化物品,再将这个大的物品和另一个泛化物品合并,直至只剩下一个泛化物品。
- 这类问题唯一易错点就是初始化问题!对于题目明显要求恰好装满或题目有意无意的暗示我们如果不是恰好的将会不合法,那么我们就应该将所有体积非零的dp值赋为负无穷。否则,所有的状态值均赋为0。
- 最后,要小心树的微妙关系。譬如:上面那道“选课”,应当将“0”作为树中根节点。在“贿赂”那道题中,子节点与父节点不允许更改之间的关系。
最后来一道水题吧!
习题:二叉苹果树
网址:https://www.luogu.com.cn/problem/P2015
题目描述
有一棵苹果树,如果树枝有分叉,一定是分2叉(就是说没有只有\(1\)个儿子的结点)
这棵树共有\(N\)个结点(叶子点或者树枝分叉点),编号为\(1-N\),树根编号一定是\(1\)。
我们用一根树枝两端连接的结点的编号来描述一根树枝的位置。下面是一颗有\(4\)个树枝的树
2 5
\ /
3 4
\ /
1
现在这颗树枝条太多了,需要剪枝。但是一些树枝上长有苹果。
给定需要保留的树枝数量,求出最多能留住多少苹果。
输入格式
第\(1\)行\(2\)个数,\(N\)和\(Q\)(\(1 <= Q <= N, 1<N <= 100\))。
\(N\)表示树的结点数,\(Q\)表示要保留的树枝数量。接下来\(N-1\)行描述树枝的信息。
每行\(3\)个整数,前两个是它连接的结点的编号。第\(3\)个数是这根树枝上苹果的数量。
每根树枝上的苹果不超过\(30000\)个。
输出格式
一个数,最多能留住的苹果的数量。
输入输出样例
输入
5 2
1 3 1
1 4 10
2 3 20
3 5 20
输出
21
这道题我挂了三次。原因在于:父子节点关系忘记了。
代码如下:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
const int maxn = 100 + 7;
struct node
{
int to, next, w;
} e[maxn * 2];
int n, q, tot = 0, head[maxn] = {};
int size[maxn] = {}, dp[maxn][maxn] = {};
void add_edge(int x, int y, int z)
{
e[++ tot].to = y;
e[tot].w = z;
e[tot].next = head[x];
head[x] = tot;
return;
}
void init()
{
memset(dp, 0xcf, sizeof(dp));
memset(size, 0, sizeof(size));
return;
}
void dfs(int u, int Fa)
{
dp[u][0] = 0;
for(int i = head[u]; i; i = e[i].next)
{
int v = e[i].to;
if(v != Fa)
{
dfs(v, u);
size[u] += size[v];
}
}
for(int i = head[u]; i; i = e[i].next)
{
int v = e[i].to;
if(v != Fa)//问题在这里了
{
for(int j = size[u]; j; -- j)
{
for(int k = j; k; -- k)
{
dp[u][j] = max(dp[u][j], dp[v][k - 1] + dp[u][j - k] + e[i].w);
}
}
}
}
++ size[u];
return;
}
int main()
{
scanf("%d %d", &n, &q);
for(int i = 1; i < n; ++ i)
{
int u, v, w;
scanf("%d %d %d", &u, &v, &w);
add_edge(u, v, w), add_edge(v, u, w);
}
init();
dfs(1, 0);
printf("%d\n", dp[1][q]);
return 0;
}


