线性代数

参考资料教程：

理论知识： https://www.bilibili.com/video/BV1Kt411y7jN?from=search&seid=84920144913588800   Gilbert Strang教授（MIT）的课！！！

直观理解： https://www.bilibili.com/video/BV1ys411472E?p=1

思想：

Linear Combination,

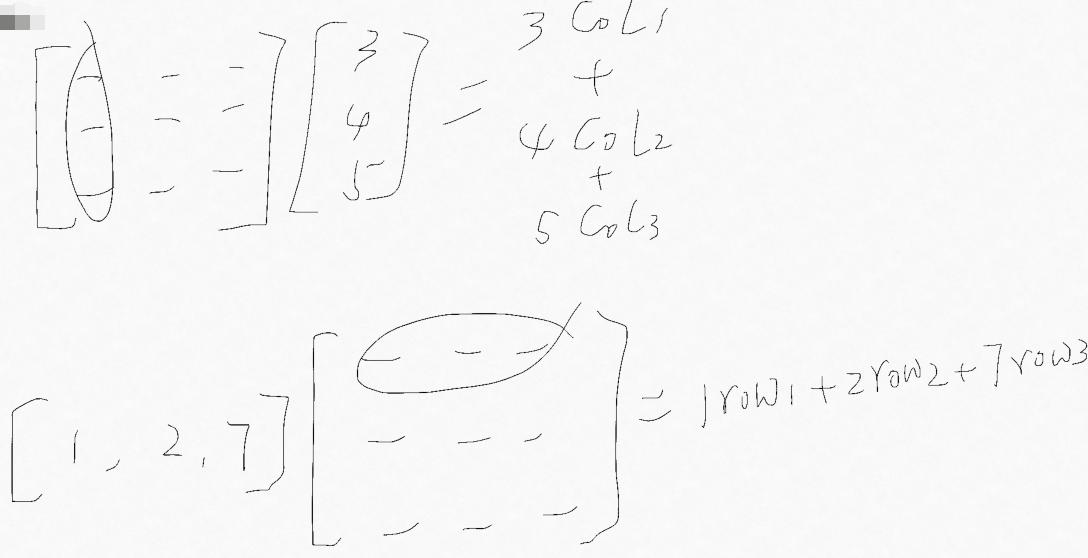
Ax = b 表达的是   矩阵A的各列的线性组合如何得到b,

核心概念：

Matrix Operation 

 

矩阵消元：

Ax = b 和 xA = b  

 

消元矩阵

 

 

 

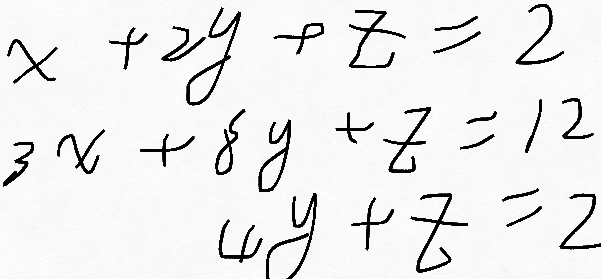
thus:

 

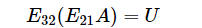
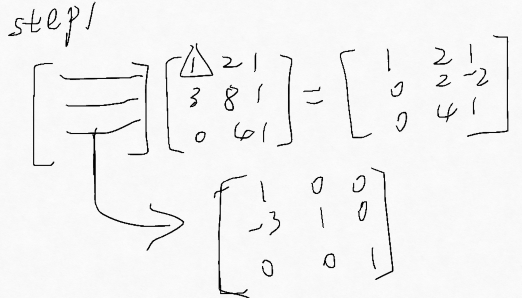
E21 表示的是要消除（eliminate）（2,1）元素为0 的矩阵

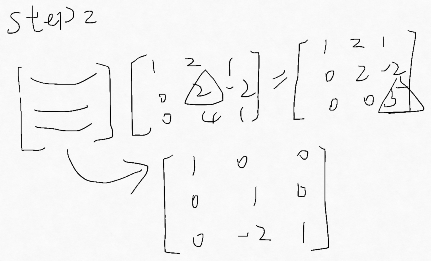
E32 表示的是要消除（eliminate）（3,2）元素为0的矩阵

最终得到U

什么矩阵可以一次性从A得到U呢？

 

矩阵乘法中虽然顺序是无法改变的，但是括号是可以移动的，

 

 

 

 

置换矩阵：

交换行

左行

 

交换列

右列

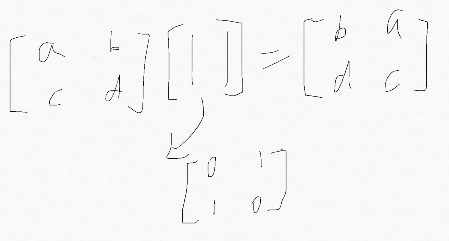
矩阵记作 P(permutation)

因此，矩阵进行行变换用左乘，进行列变换用右乘。这也说明了矩阵乘法中 AB 不等同于 BA  

逆矩阵：

 

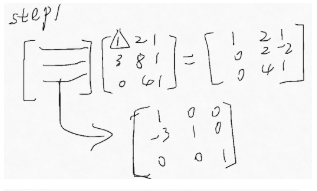
如何取消这一步的消元呢？

其实只要将 E21 消元矩阵 变为单位矩阵即可，

 

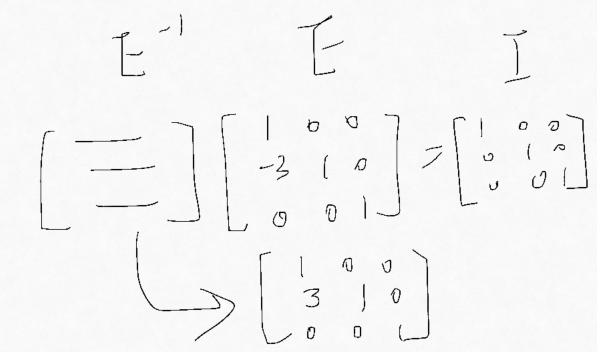
就是它的逆矩阵，

矩阵乘法：

四种方法：

常规方法（一行乘一列得到一个数），列方法，行方法，一列乘一行得到矩阵

4th way:

 

 

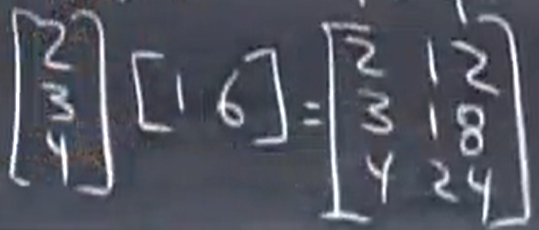
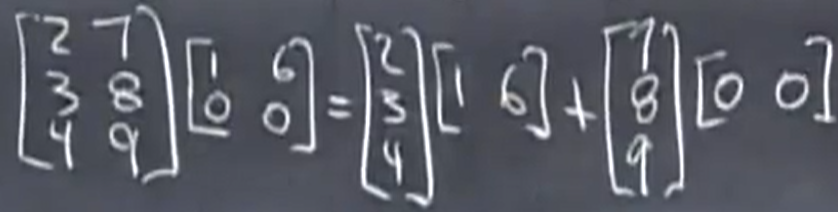
也可以将矩阵切成块，对块进行乘法：

 

 

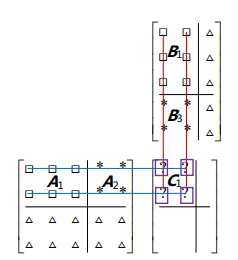
逆：

如果矩阵 A 是方阵，若存在逆矩阵 A-1，使得 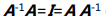（左逆矩阵等于右 逆矩阵）我们称矩阵 A 可逆（invertible）或者矩阵 A 非奇异（non-singular）。.如果不是方阵，左逆就不等于右逆了，因为形状不同，无法运算。 

 

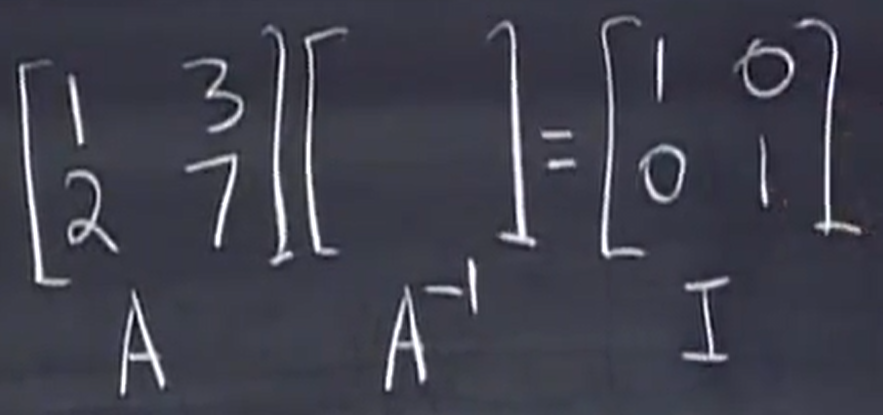
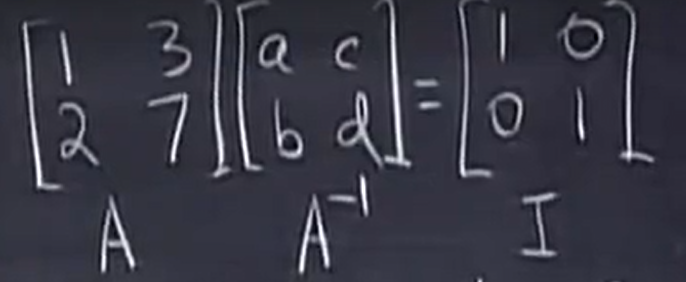
这里使用Gauss-Jordan(同时处理两个方程组),

如果考虑单个方程的话应该是如下情况：

 

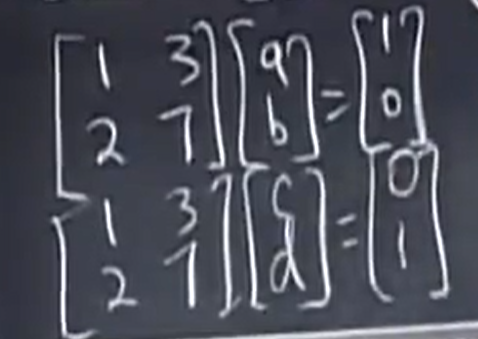
此时Jordan对Gauss 说，你把两个合一起吧!  就是如下：

 

 

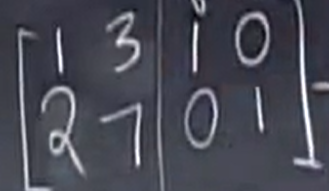
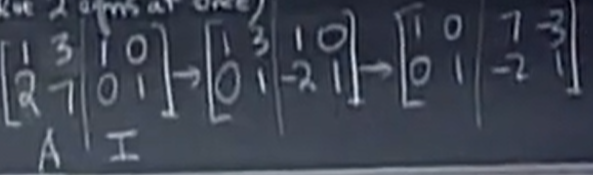
为什么这样做可以得到A的逆呢？

上述的过程矩阵表示是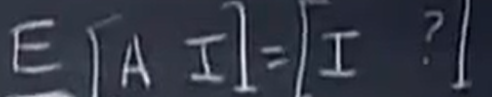：（E指的是消元矩阵（eliminate），这里其实是由两个E得到的，因为两步）

 

采用分块的思想，

第一部分EA=I ,所以E就是A的逆。 

第二部分EI = ?, 所以？也是A的逆。 

 

not-singular 当然很好，但是singular 也是存在的，

下面讨论singular 没有逆的情况，

 

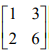
为什么它没有逆（不可逆）呢？

解释一：假设该矩阵乘以一个矩阵得到单位矩阵，使用列的方法，单位矩阵中的第一列【1,0】，肯定是要由列【1,2】 和【3,6】线性组成的，容易知道，这是不可能实现的。

 

解释二：因为我们能找出一个非零向量x  使得 Ax = 0   .x就是列向量[-3,1],或者[1,-3]。 这为什么可以说明它没有逆呢？因为如果A存在逆的话，我们用A的逆乘 Ax =0 这个方程就得到  A'Ax = 0，即x = 0; 形成矛盾。 

 

矩阵的LU分解：

本节的主要目的是从矩阵的角度理解高斯消元法，最后找到所谓的 L 矩阵，使 得矩阵 A 可以转变为上三角阵 U。即完成 LU 分解得到 A=LU。可以将矩阵的分解类比为多项式的 因式分解，分解后的结果可以让我们更容易看清“解”的状态

知识点1：

假设A，B均可逆，AB的逆是什么？相当于问  AB__  = I ? 容易知道答案 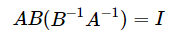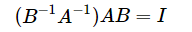,所以AB的逆应该是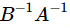

知识点2：

 

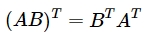
直观上理解如下：

 

知识点3：

一个矩阵转置之后的逆矩阵是什么呢？？？

我们知道 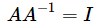,现在对这个方程左右同时进行转置，

 

容易知道单位矩阵I转置之后还是单位矩阵，

所以，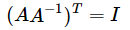

 

所以，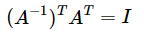

 

所以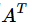，的逆矩阵是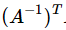

 

总结，A的转置的逆就是A的逆的转置。  

换句话说，对于单个矩阵，转置和逆两种运算，先后次序可以颠倒（即对一个矩阵，先转置后求逆 和 先求逆后转置 是一样的效果）。 

知识点4：

A = LU  ，这里的L指的是lower 下三角，U指的是upper 上三角。

 

E21应该是[ [1,0 ] ,[-4,1 ] ]

 

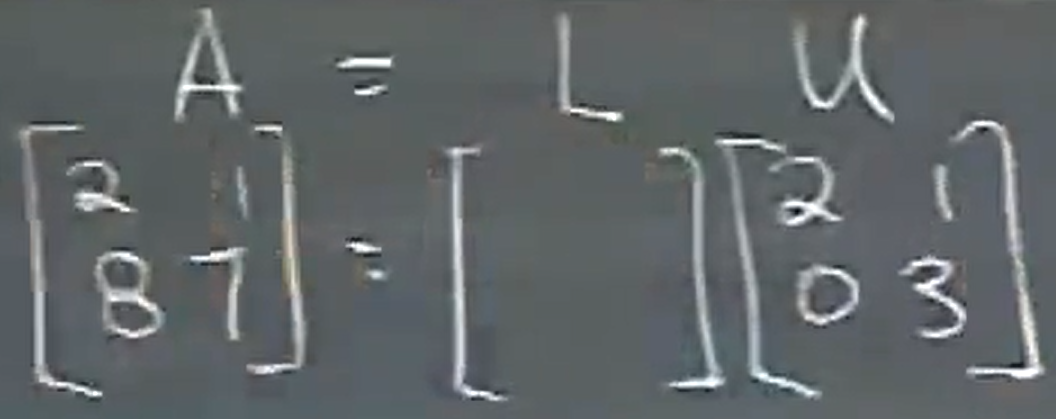
首先这个L，应该是E21的逆，

L 应该是[ [1,0 ] ,[4,1 ] ] ，因为这里是2x2矩阵，所以E和L的差别不大，

下面看3x3的矩阵：

假设A是3x3的矩阵，左面乘以消元矩阵，如下：

 

 

A = ______ U ,这里应该填什么呢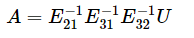？ 即A = LU 

 

 

问题：

或许你会问为什么用逆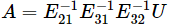（）的形式呢？非逆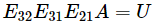（）的形式不好吗？ 

 

 

答：

 

 

 

 

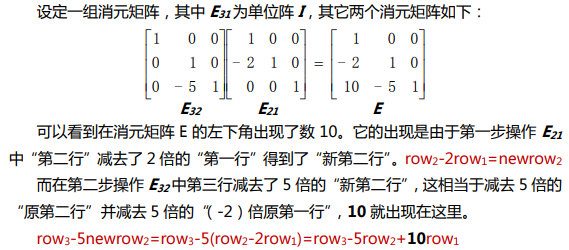
如果没有行交换操作，则消元矩阵的因子   可以直接写入矩阵 L。

所以A= LU 优于EA=U

知识点：

How many operations on  nxn matrix A? A 经过多少次的计算才能得到U呢？

消元法所需要的运算量？（注：一般，乘法之后再减法算是一次operation）

在一些应用中我们需要处理超大型矩阵，即使用计算机来处理这一问题，也需 要评估所需的计算量。

如果我们把“先乘后减”大致记为一次运算，那么对于一个 nxn 矩阵，对第一行消元大概需要n^2 （精准的说是n x (n-1)  ），

以此类推。 最后需要的运算次数为 n^2 +... + 1^2，利用积分公式可以估算其数值。

等号右侧向量 b 的行变换大致需要 n^2(n+1 + ... + 1)次运算。

行交换 Row exchanges

上面都是默认不用行交换，

如果主元的位置出现了 0，就需要进行“行交换”。我们可以通过左乘一个交换矩阵（Permutation Matrix）实现“行交换”的操作。

例如：

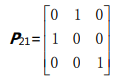
所有的交换矩阵（3x3）如下，数目是：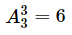  

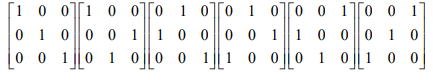分别是0交换，2,3,交换,1,2交换，等等... 

如果它们之间互相乘得到的结果仍然在其中，就是在行交换。

而且它们每个的逆也都是它们自身。

还可以说每个的逆就是它们本身的转置。 

这就是一个矩阵群（group）. 

交换（permutations）、转置（Transposes）和空间（spaces）

本节的将引入向量空间（vector spaces）和子空间（subspaces）。

交换Permutations

同样考虑A  = LU ，之前都是不考虑进行行交换，现在考虑。

当应用消元法求解方程组的时候我们需要通过行交换将 0 从主元位置移走。左乘一个交换矩阵可以实现行交换的操作。（为了满足数值计算的要求，Matlab 甚至会 对接近于 0 的非零主元做行交换）因此我们的 LU 分解由 A=LU 变为 PA=LU。其中的 P 就是对 A 的行向量进行重新排序的交换矩阵。

交换矩阵 P 是通过对单位阵进行“行交换”得到的。对于 nxn 矩阵存在着 n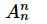！（）个交换矩阵。置换矩阵具有特殊性质: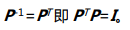 

 

 

 

转置 Transposes

直接上个例子：

 

 

 

 

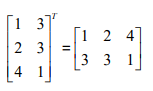
 用符号表示就是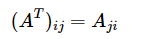  

 

 

知识点   对称矩阵（Symmetric Matries）

它其实就是 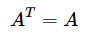,举个例子就是，

 

 

像具有这种转置不变性质的矩阵就是对称矩阵。 

 

知识点

的转置是，它们二者相乘就得到的就是对称矩阵，这是为什么呢？

 

 

is always symmetric !!! why???

TAKE A TRANSPOSE（转置）！！！

 

 

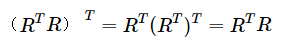
向量空间 Vector spaces

What are Vector-spaces ? What are Sub-spaces?

我们可以对向量进行所谓“线性运算”，即通过加和（v+w）与数乘运算（3v） 得到向量的线性组合。这两种运算是向量空间中所要用到的，

需要特别指出的是这里的spaces 指的是 很多很多向量，一整个空间的向量！

从例子开始，

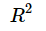（读法： R two 不读R 方）,说明我们讨论的是实数，向量用两个实数表示。 

 R2 = all 2-dim real column vectors（无法完全列举），简单举例是

 

 

       = x-y plane

 

 

 

注：0,0 一定是要的，如果去掉0，0 ，x-y 平面就想是被扎了一个窟窿一样。

为什么一定要0,0向量呢？

因为对于向量空间，一个向量进行加和 数乘之后一定还要属于该向量空间， （3,2）乘0后得到就是（0,0），（3,2）加上（-3，-2）也是（0，0）。所以一定需要（0,0）的存在！

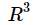 R three, 

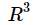=all 3-dim real column vectors .例如： 

all n-dim real column vectors.  

向量空间需要满足的要求

向量空间必须对数乘和加法两种运算是封闭的，（例如，二维平面，第一象限中的向量进行数乘就可能回不到第一象限，所以第一象限就不是向量空间）

 

问题？什么样的空间，虽然只是R2的一部分，但是不管加法还是数乘，结果依然在此空间内？

这就是Sub-Space!

子空间 SubSpace:

 

这个直线就是向量空间（SubSpace）,任意取一个向量，数乘任何都可以还在此向量空间；检验加法也是如此，取一个向量加上另一个向量结果仍然还是在此向量空间，所以满足向量空间要求。 

需要注意的是该直线必须要通过原点！ 

R2 中不穿过原点的直线就不是向量空间。子空间必须包含零向量，原因 就是数乘 0 的到的零向量必须处于子空间中。

 

R2 的子空间都有哪些呢？

 

 

 

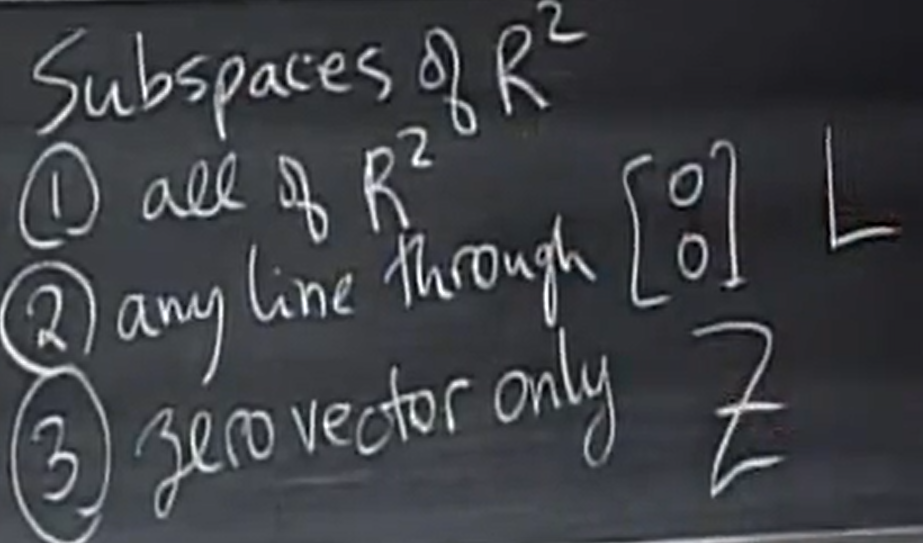
矩阵是如何构造子空间的呢？

 

 

这个subspace 有个名字，叫做Column Space（列空间）。可以记作C（A）.C 是 coumn的意思。 

画图表示：

 

如果恰好两个col vector 共线，那么column space 就变成了一条直线！

列空间和零空间

我们知道在R3中，L（通过原点的直线）是R3的子空间，P（通过原点的一个平面）也是个R3的子空间，那么L 和P的并集（LUP）还是R3的子空间？

No! （因为并集中加法是不封闭的，）

那么交集呢？P 和 L的交集呢？对于R3，它们的交集是原点，是子空间！

那么对于任意的两个子空间的交集呢？它们也是对应的子空间！

 

列空间 column space:

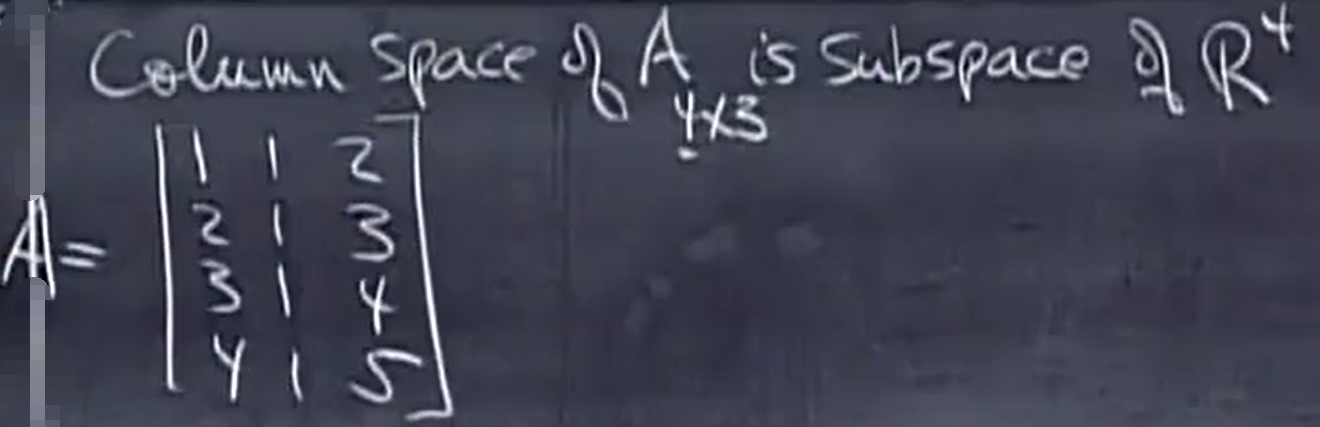
A这三个列向量可以完全组成R4空间吗？ 肯定是不能的！

 

 

 

  No ,Why? 因为有4个方程，却有3个未知数，

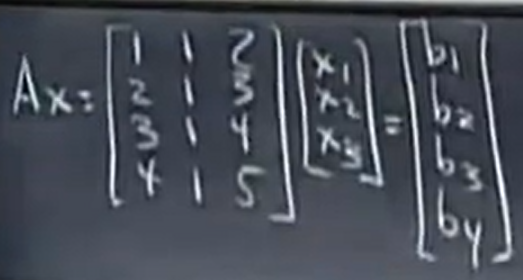 这个方程组不总是有解的，因为3个列向量是无法填充真个R4空间的，所以有大量的b1,b2,b3,b4 不能由这三个列向量的线性组合~

 

 

那么上面方程组什么时候可能有解？什么样的右侧向量b可以使得方程有解呢？

你可能随口说出，所有的b都为0，方程就有解了，解也都是0 。

那再说个，可以使得方程有解的b?

b 是 1，2，3,4,此时也有解，解为 1,0,0   

b 是 1,1,1,1,此时也有解，解为 0,1,0   

b 是2，3,4,5此时也有解，解为 0,0,1   

于是，上面的问题的答案就是：只有当b是各列的线性组合的时候（b在A的列空间中），Ax=b才有解。 

 

另一个问题：我们能去掉其中的一列，构造同样的列空间吗？ Yes! ,例如，去掉第3列，

再问？去掉第一列可以吗？当然也可以，我们的习惯一般都是考虑靠前的线性无关向量。 

因此，A这时形成的列空间可以描述为  R4中的二维子空间！

 

零空间 null space:

矩阵 A 的零空间即满足 Ax=0 的所有 x 构成的向量空间。

零空间是一个完全不同的子空间，它是不包含右侧的b向量， 它包含x向量。  

 

 

A的列空间是在R4的，A的零空间是在R3 的，

首先说一个解，0,0,0

再说一个解，那就是1,1，-1 

再说一个解, 2,2,-2 ，其实归纳就是 c,c,-c

一个式子表示就是：

 画出它的图像就是R3中的一条通过（0，0,0）的直线

 

 

构建子空间的两种方法：

1，给出几个向量，通过线性组合，然后得到子空间。例如本例A矩阵的列空间。

2，也可以从一个方程组中，通过让x满足特定条件来得到子空间。 例如本例A矩阵的零空间。

对于 mxn 矩阵，列空间为 Rm的子空间， 零空间为 Rn空间的子空间。

求解 Ax=0

我们定义了矩阵的列空间和零空间，那么如何求得这些子空间呢？本节课的内 容即从定义转到算法

计算零空间 Nullspace

AX = 0

 

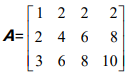
我们对其进行消元，消元的过程其零空间是不会变的，因为解不变，（实际列空间会改变）！ 

 

rank（秩） of A = number of privots (主元的数目)  = 2  

现在方程变为了UX =0 

 

privot columns 和 free columns 如下图：

 

 

为什么称之为free columns ?

因为可以自由给x2,x4 赋值，列2，列4的乘数是任意的，  

不妨取x2 = 1 x4=0 ,则解为[-2,1,0,0]  它即在矩阵的零空间中，  

再取x2 = 0 x4=1 ,则解为[2,0,-2,1]  它也在矩阵的零空间中，  

我们求出的这两个向量称之为 特解 。 

 

零空间正好是所有特解的线性组合，  那么有多少个特解呢？每个自由变量对应一个特解， 那么有多少个自由变量呢？

rank = 2 ，意思是主元（主变量）为2  ，所以自由变量是 4-2 = 2  ，如果对于 Amn ，自由变量是 n -r 个！

 

上面的矩阵形式：我们称之为 row echelon form (行阶梯形式)，

 

我们可以进一步简化，变为 reduced row echelon form (简化行形势)

我们可以将主元上下都变为0 ，

 

我们还可以将主元变为1 ，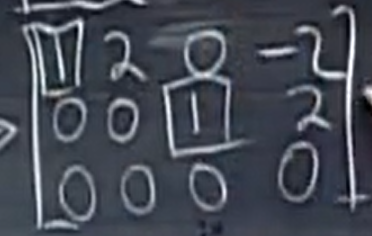

 

这个矩阵以最简的形式表达了矩阵的相关信息，   这个矩阵记为R，（RX=0）。  

 

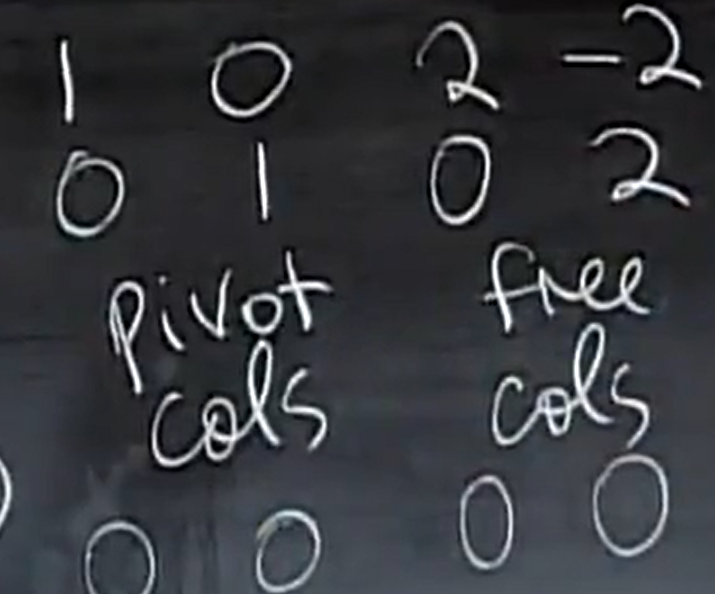
这和最终的解是不是很像呢，

 

 

假设矩阵已经是rref 形式，

 

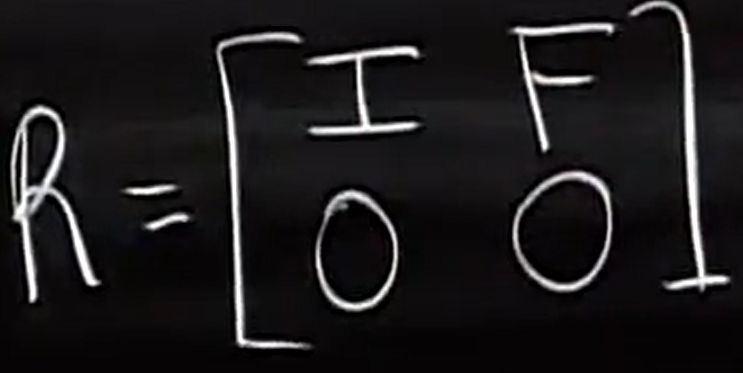
I 是 rxr 的单位矩阵， F 是 rx(n-r)的自由矩阵  

现在求解 RX= 0 ，它的特解是什么呢？

记N为零空间的向量， 

RN = 0 ,

那么N是什么呢？ 

 

 

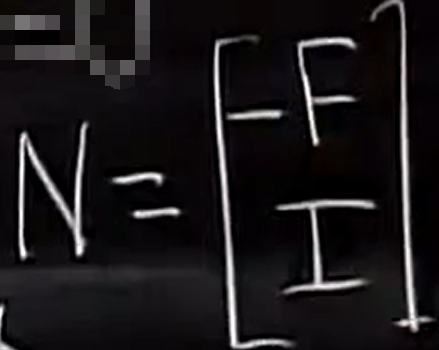
对于矩阵 R 而言，求零空间（RX=0）就变得非常简单，只需要将消元的到的 F 部分 拼接上单位阵就可以得到所有的通解。

注意如果在变换出 R 左上角的单位阵的过程 中采用了列交换，则最后的解要完成逆变换

 

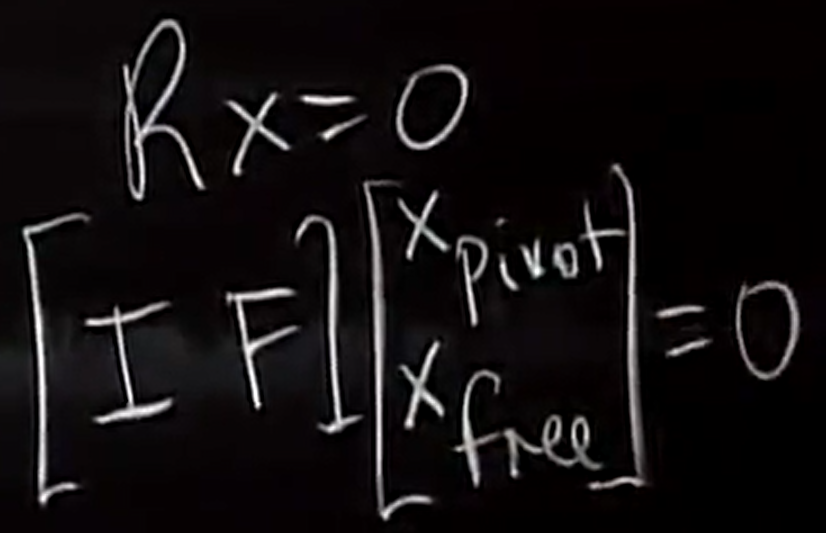
即，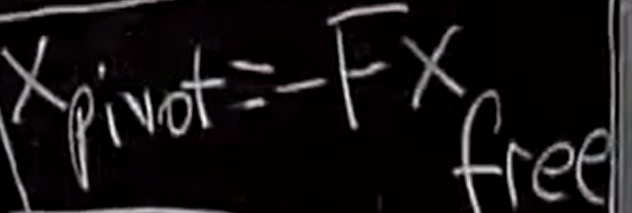

 

 

再看一个例子，

 

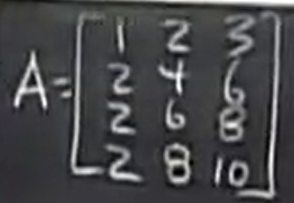
它有 2  个主元变量， 这个矩阵的特解有n-r ,3-2 个特解，  

下面得出 零空间是什么？

令x3=1, 得到 【-1，-1,1】

所以整个零空间是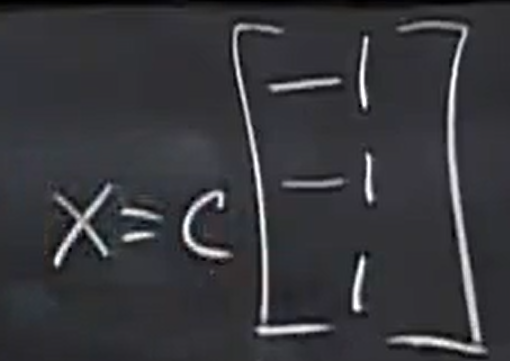

 

 

这个矩阵的 rref 形式 R 为： 

 

 

 

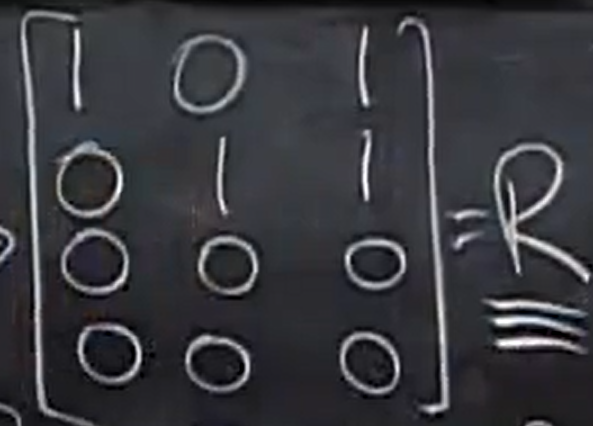
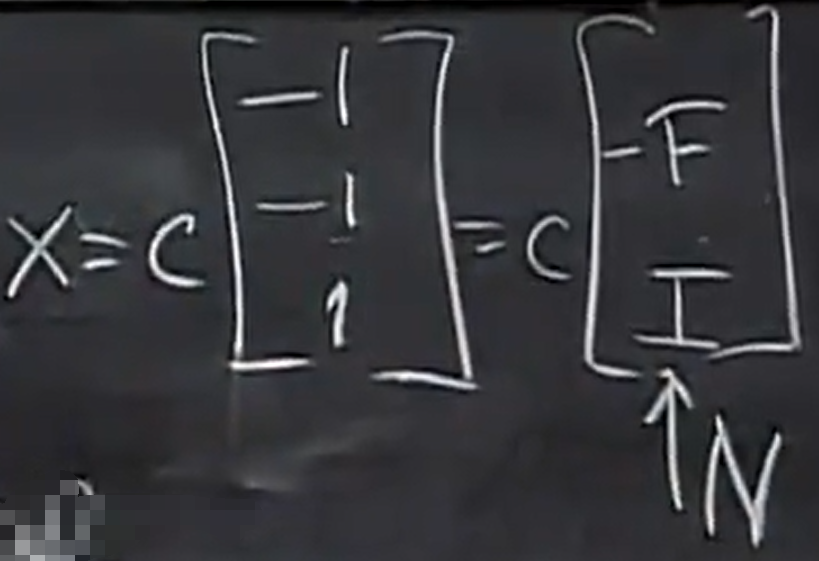
求解 Ax=b

 

它可能有解，也可能无解，这要通过消元来确定

有解的话，要确定是唯一解还是很多解， 

 

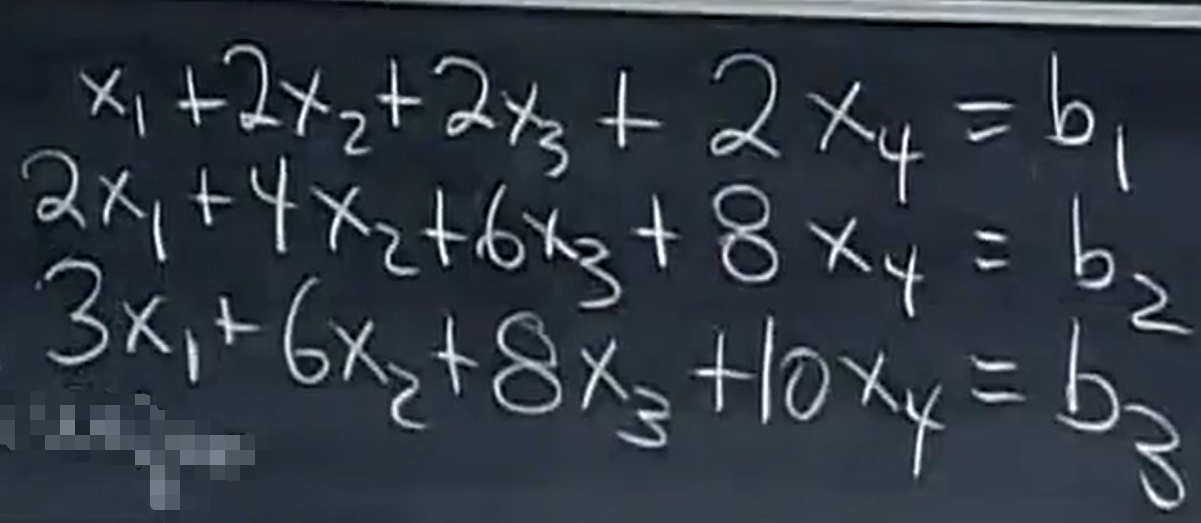
如果方程组有解，b1,b2,b3 需要满足什么条件呢？ 需要满足 b1 + b2 = b3 .  如果左侧的行的线性组合为0 ，那么右侧的对应的线性组合也必然为0 。 

写出增广矩阵，如下： 

 

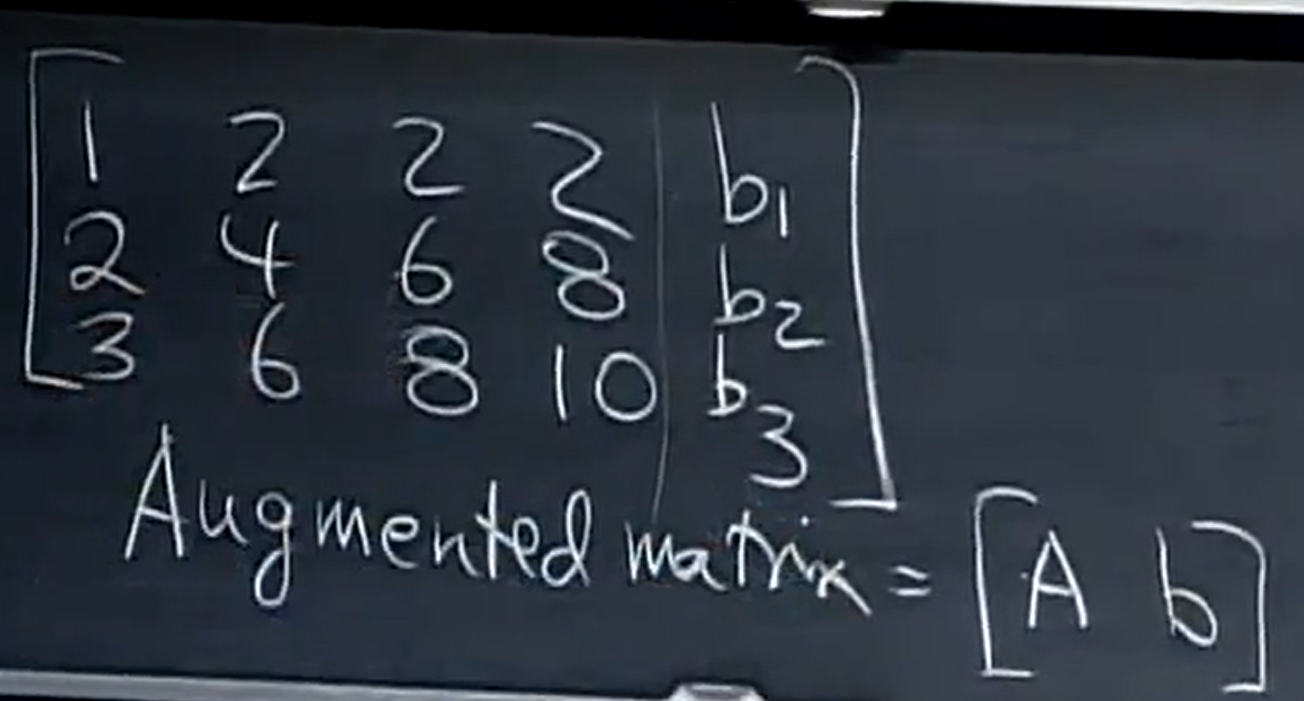
消元得： ，于是：看第三行， 0 = b3-b2-b1 。  所以这就是有解的条件。  

 

 

AX =b 有解的条件：

用列空间描述，

b 必须属于A的列空间， 也就是 b必须是A各列的线性组合， 

另一种描述方式， 如果A中的行线性组合得到0，那么b对应的线性组合也要得到0 。 

 

有解，继续求出具体的解：

找出AX=b 的所有解， 

 

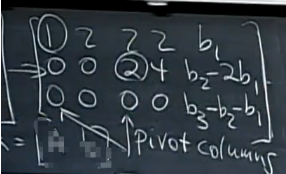
假设b向量为【1,5,6】

 

先求特解  Xparticular：

设定所有的自由变量为0 ，  然后解出Ax=b 的主变量，，所以x1 = -2, x3= 3/2 .     x=（-2，0,3/2,0。（列形式）。这是一个特解。    

 

再求Xnullspace：

所以，最终的解是，X = Xp + Xn , 为什么是这种形式呢？  

原因如下： 

 

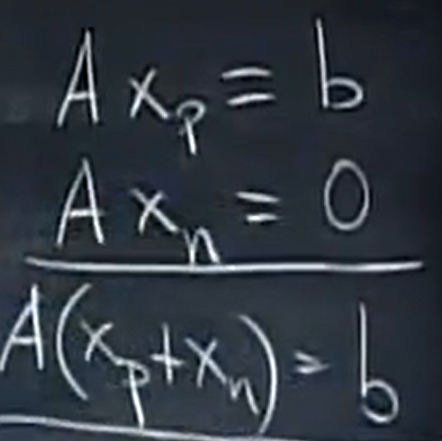
对于方程组（有解）的某个特解，它与其零空间内任意向量之和仍为解。 

对于这个例子来说，

 

这个Xcomplete 不是向量空间， 后面的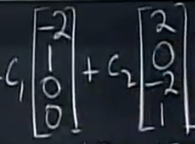算是子空间，是R4中的二维子空间，  

 

 

更高维度的讨论：

对于  Amn 秩为 r , r  和 mn 的关系： 肯定有 r ≤ n ,r≤ m , 

满秩的情况：  

1， 列满秩（Full column rank ）

即r = n ,  列满秩，每一列都有主元。  主变量有n个，  自由变量是0 个，

这个时候的零解是什么样？通解又是什么情况？  

此时的A 的null space ， N(A )  只有零向量，因为此时没有自由变量可以赋值。  所以A的零空间，只有一个零向量。 

此时AX=b 的解，就只有一个特解Xp了（如果有解的话），X=Xp  ,

总结： 列满秩时，如果存在解的话，那么解唯一（unique）! 换另一种表述方式，此时，只有0，或1个解。 

 

举例：

 

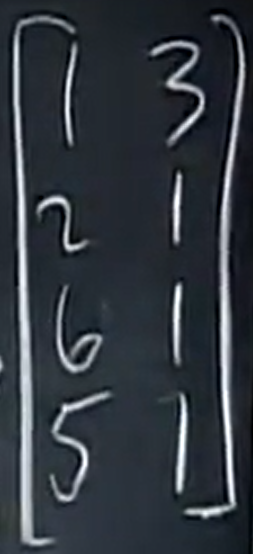
它的r = 2 .   

 

此时的零空间只有 0向量一个，这里要问的是：是否Ax=b 总有解？  不是，当b刚好在A的列空间才有解，  

例如b= [4,3,7,6] ,此时的解为【1,1】（列）

2， 行满秩（Full row rank ）

r = m , 此时主变量个数为m, 自由变量为 n -r,n-m 个。  

此时b取什么，Ax=b 有解，  此时消元时不会出现零行了，  所以，此时b没有了要求，  所以对于任意右侧向量b，Ax=b 都有解，  

例子： 

 

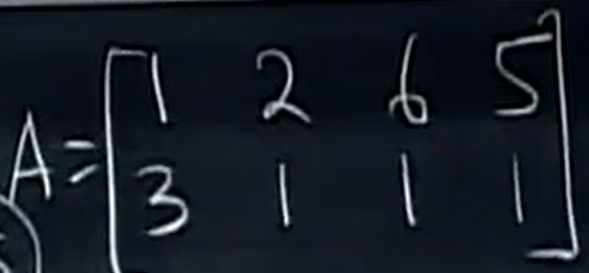
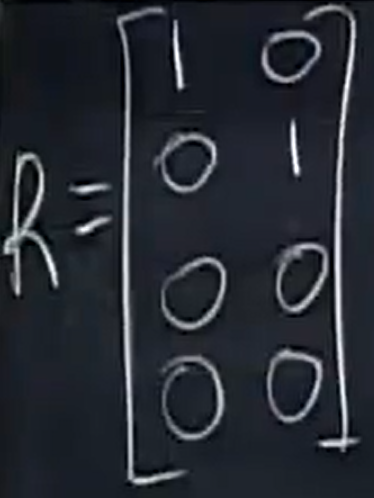
它的秩是2，  

 

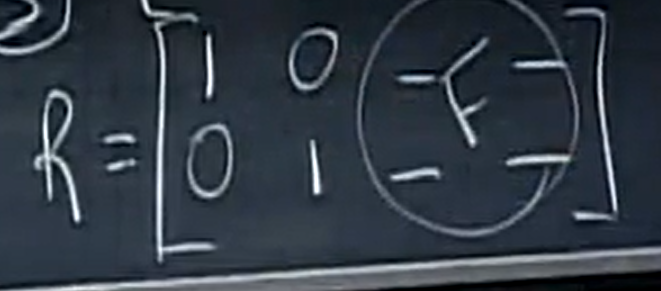
此时，自由变量可以自由赋值，所以此时零空间也不知是0向量，所以必然有解， 

 

3 ,最后 r = m = n :

 

 

 

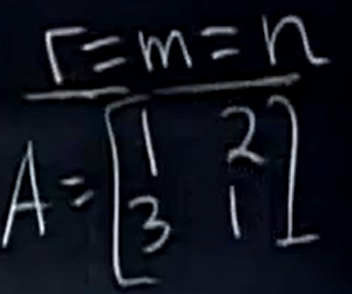
它的零空间是什么呢？ 自由变量个数为 n-r = n-n = 0 ,所以它没有自由变量可以随意赋值，它的零空间只有一个零向量。 

Ax=b 有解的条件是什么呢？因为它没有零行，所以它的b没有限制，任何b,Ax=b 都有解，  

 

总结： 

 

矩阵的秩决定了方程组解的数目，  

线性无关，基和维数（Independence, basis, and dimension）

对向量组而言，什么是线性无关？

什么是向量空间的基？

什么是向量空间的维数？

线性无关

什么时候 向量x1,x2,x3,...xn 是线性无关的？  

存在结果为0的组合？除了系数全为0，如果存在一种组合可以使得结果为0，那么它们就是线性相关的。 

所以，上面的答案是：

除了系数全为0之外，如果不存在结果为0向量的组合，则这些向量是线性无关的。 

举个例子：

1,

 

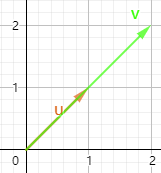
此时u 和v 必然是线性相关的，v = 2u 即 v-2u=0 

2,

 

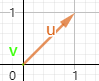
此时，v是0向量（0,0），也是线性相关的，因为存在 2v+0u = 0; 等等... 

3,

 

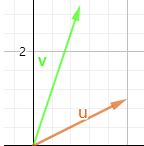
 此时,u,v 是线性无关的，因为除了 0u+0v =0之外，再也找不到可以使之为0的系数了。 

 

4，

 

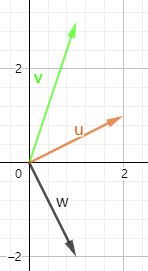
此时u,v,w 是线性相关的， 因为它们存在着某种组合使    ,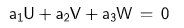

 

那为什么3个二维向量一定存在某种组合使？？？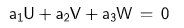

因为：

我们可以构造如下矩阵  

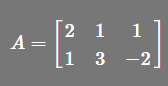 （  三列为： u,v,w） 

容易知道A是 2x3 ，由之前的知识知道 m <n 的，所以它存在自由变量，所以Ax=0 的解会存在非零解~ 

 

 

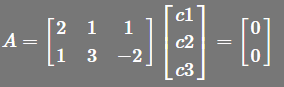
对于一个矩阵，我们对其中的各列是相关还是无关感兴趣，如果A的零空间N（A）存在非零向量，那么各列相关。即 A的零空间N（A）只有0向量的时候，那么各列线性无关。 

 

下面考虑矩阵的秩，

如果矩阵的列向量线性无关，那么矩阵的秩是多少呢？

这时候所有的列向量应该都是主列，此时不存在自由变量，所以此时的A的零空间也就只有0向量。 （自由列的实质是主列的一些线性组合，所以不应该存在它们）

所以此时的rank = n；  

so,

当矩阵的秩 =n ，此时列向量线性无关；（没有自由变量）

当矩阵的秩<n ,此时列向量线性相关；（有自由变量）

 

 

span a space:

Vectors V1,V2,...Vn  span a Space 的意思是：生成的这个空间包含了 vectors 中的所有线性组合。 

换种说法： 把向量组的所有向量的线性组合的结果放到一个空间里面， 就是Span a space. 

 

给定一个矩阵，那么它里面所有的列向量可以得到这个矩阵的列空间，这时问，矩阵的所有列向量都是线性无关的？回答是 ，可能是，也可能不是，

不过，我们喜欢的是：

它们既可以生成所需的Space,它们本身也是线性无关的，

这就意味着 列向量的数量必须得当，如果数目少了不能生成所需的空间，如果数目多了，它们之间又不能满足线性无关，

So, 引出了基的概念，它包含的向量的个数不多不少。

基（向量空间的基，basis）:

向量空间的基 指的是 一系列向量，   v1,v2,v3,...vd,  

这些向量需要满足两个特点：

向量的个数不多也不少， 生成所需的空间，并且自身线性无关。 

举个例子：

假设空间是R3,什么是三维空间的基呢？

求空间的一组基，相当于要找到一组向量， 

最容易想到的是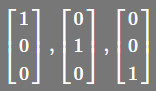： ，它们可以span R3 ，而且它们本身也是线性无关的（rank = n）

 

再来一组： 它们本身是线性无关的（rank=n）,但是它们不能span 完整的R3,

再来一组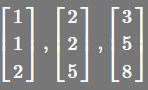：，它们本身线性无关，也可以构成完整的R3,

 

所以，R3的基有无数，只要是本身线性无关，也可以构成完整的R3就行，  

但是这所有的基都有相同的特性，  对于给定的空间，该空间的基的向量个数是一样的，R3 空间个数为3， 我们应该 称 3这个数字（基的向量的个数）为 维数， 即为空间的维数，  

 

例子：

 

 

讨论列空间：

它们能生成矩阵的列空间？ 当然可以

那它们是矩阵的列空间的基？ No, 因为矩阵的零空间不只有0，  

请说该列空间的一组基，easy， 前两列向量就满足条件，

 

该矩阵的秩是多少？ 是2， 因为矩阵的秩就等于主元的个数，即主列的数目，也即是 该矩阵的 列空间的 维数 。 注：不是该矩阵的维数，

矩阵的秩  r  =  矩阵主元列的数目  =  矩阵的列空间的维数

我们也不会说列空间的秩，因为矩阵才有秩， 

 

讨论矩阵的零空间，

本例中矩阵的列向量不是线性无关的，因此其零空间 N(A)不止包含零向量

零空间的维数是多少呢？

通过给自由变量赋值0,1， 得到两个解：

 

这两个特殊解是否构成了零空间的一组基？答案是yes,  

零空间是2维的， 

零空间的维数是自由变量的数目 = n - r  。

 

矩阵的四个基本子空间：

前面已经说过两个：列空间 和 零空间， 

4个子空间：

列空间 ：C（A）  in  Rm    dim(  C(A)  ) = rank    ，

零空间： N(A)   in  Rn ,  dim(  N(A)  ) = n - rank  自由变量的个数

行空间：R(A)，但是一般我们用列向量，所以进行转置，即C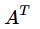（）   in  Rn  ,    dim(  C(A^T)  ) = rank     

左零空间，即 N(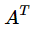) . N 指的是 Null ，通常称之为 左零空间，  in Rm ， dim(  N(A^T)  ) = m - rank  自由变量的个数  . 注：dim 是维数，也就是基中向量的个数

 

4个子空间的基：

1，

列空间C（A）：一组基：化为R得到的主列对应的A中的列就是一组基，

行空间C（A^T）：一组基：化为R得到时，主行就是一组基，  

 

Note : A -> R , 列空间发生变换，行空间没有发生变换，  

 

 

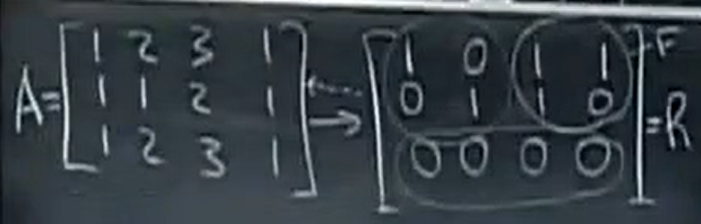
注： C(A) != C(R),    C(A^T) = C(R^T)， 即列空间改变，行空间没变， 

 

2，

左零空间， N(A^T)

A^T y = 0 ,那么y 就在左零空间内， 

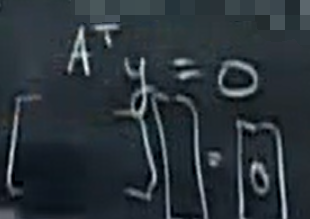
下面把y 放到左面， 对方程进行转置， 

 

 

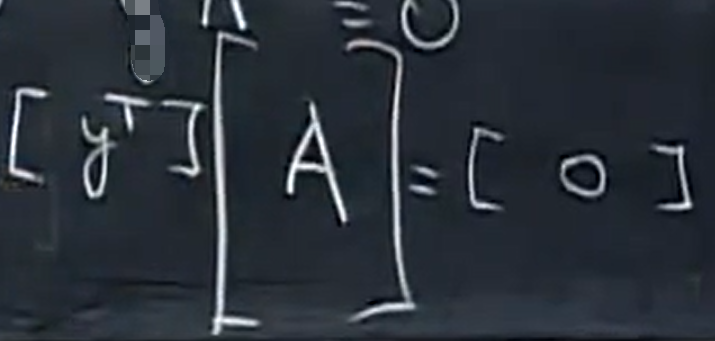
这就是为什么叫它  左零空间  的原因，

如何求左零空间的基呢？

 

如何乘一个矩阵快速从A得到R呢，

 

 

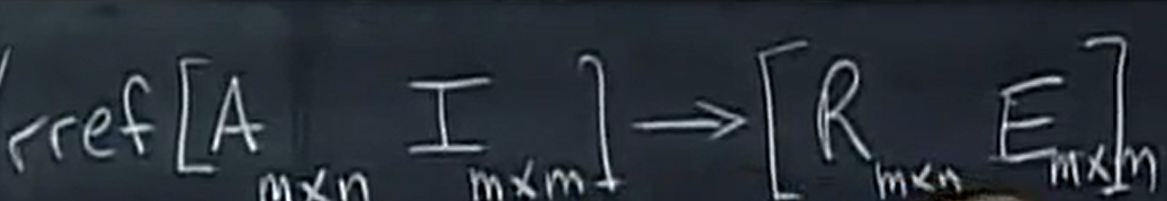
里面的Emxm 它起到的作用其实将A到R的 整个变换过程给完整的记录下来，也就是我们要找的矩阵，  

其实就是：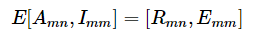 

 

 

也就是EA = R  

 

 

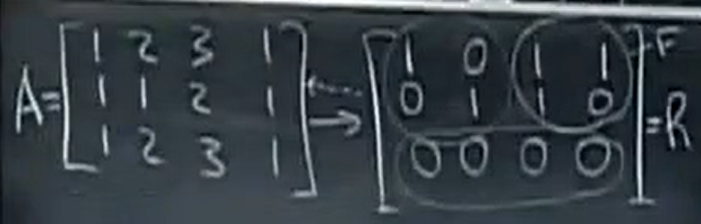
所以A的左零空间的一个基就是E中的第三行，  

 

新向量空间 New vector space，把整个矩阵看做“向量”：

我们之前了解的向量空间都是3维或者n维 的实数空间， 现在我们了解一个新类型的向量空间， 

把整个矩阵看做“向量”，矩阵和矩阵可以数乘，也可以加和，（暂不考虑乘法）。

所有 3x3 矩阵构成的集合是一个向量空间，符合对于线性运算封闭，称之为 M

M 的子空间包括：

　　• 所有的上三角阵 

　　• 所有的对称阵

　　• 所有的对角阵

对角阵是前两个子空间的交集,所以它更小，  

简单问题，对角阵的维度是多少呢？3，

写出对角阵的一组基如下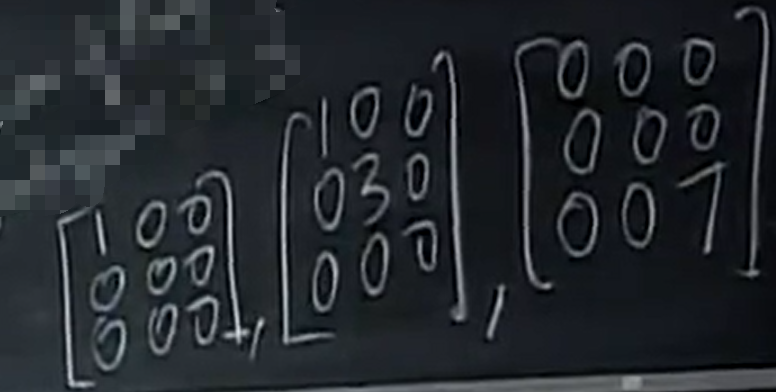：   ，它们是相互 线性无关的， 任何的 对角矩阵都可以由这三个组合而成，

这种思想就好比是将之前的 Rn  延伸到了 Rnxn  

矩阵空间、秩 1 矩阵和小世界图

之前说的空间都是向量空间，这里要说的矩阵空间是把整个矩阵看做是一个“向量”，然后它们线性组合也能得到一个“向量”空间，这里我们称之为矩阵空间。 

 

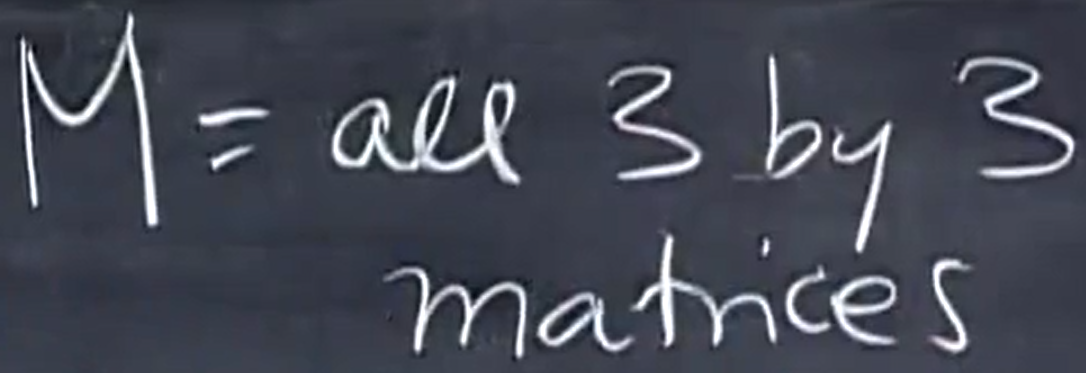
注意：乘法和向量空间没关系，仅仅考虑加法和数乘， 

 

M 的一组基：

 

M的子空间：

对称矩阵 Symmetric

上三角矩阵 uppertri 

对角矩阵 diagonal  

dim M = 9 

dim Symmetric = dim S = ?    应该等于6，   

dim Uppertri = dim U = ?  应该也是6 ，

对称矩阵和上三角矩阵的交集的维度是多少？

 

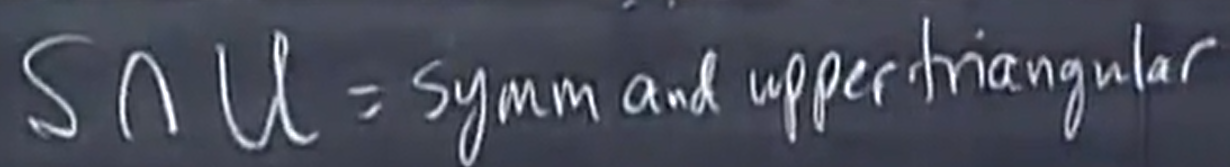
首先，矩阵必须是对称而且是上三角的， 那么它是个对角矩阵， 所以S交U的维度是3， 

 

对称矩阵和上三角矩阵的并集的维度是多少？

这就不太好了， 这就相当于一个直线和一个平面的空间，可能会组合出不在该平面和该直线的其他向量， 

 

对称矩阵和上三角矩阵的  和  的维度是多少？

加起来， 它是取 S中一元素和 U中一元素加起来， 我们得到了一个什么样的矩阵空间？

可以得到所有的矩阵，所有的3x3 矩阵， 

dim(S+U) = 9  

 

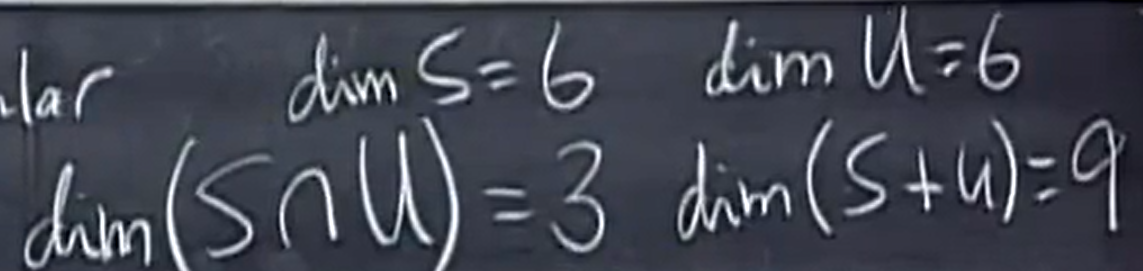
即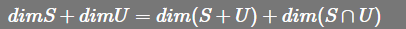：  6 + 6  =  9 + 3  

 

 

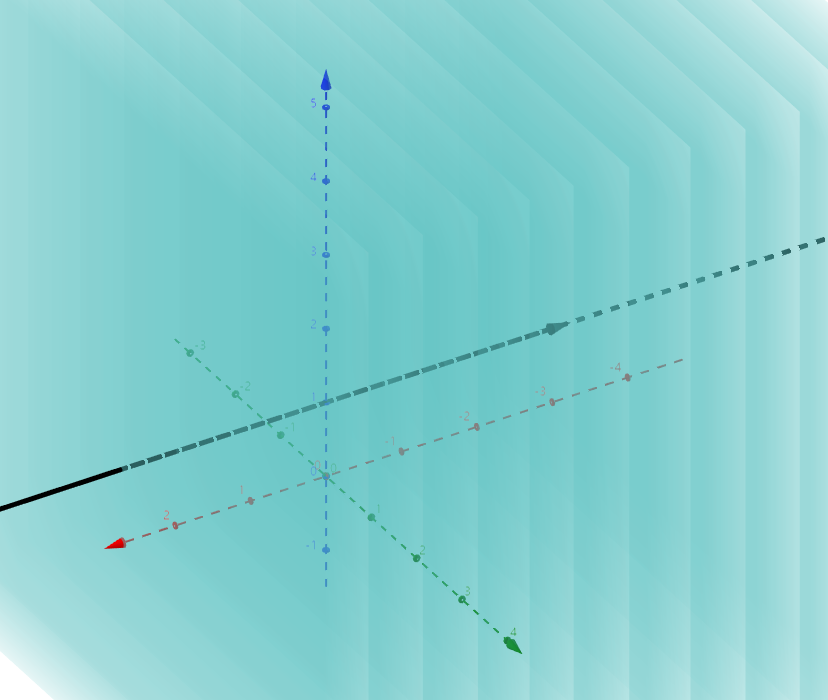
就像直线和平面加起来一样，如下图：

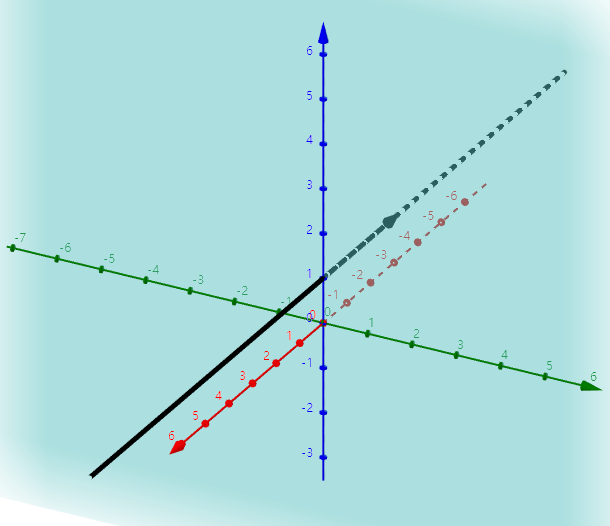
加起来之后可以得到整个空间，

 

 

秩为1 的 矩阵

 

 

 

 

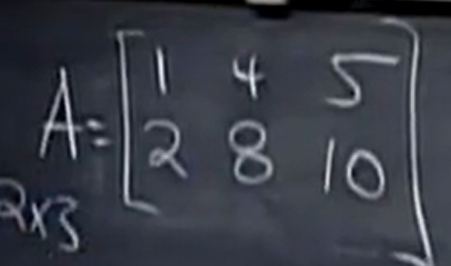
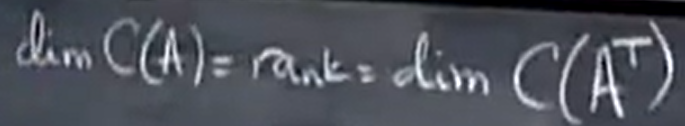
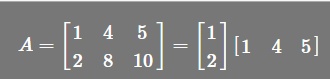
想要表达的是

所有秩为1 的矩阵，都可以表示为一列乘以一行的形式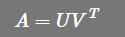，(u,v 都是列的形式） 

 

秩 1 矩阵的行列 式和特征值都很简单，它可以被当作是构建其他矩阵的“积木”。其实我们在矩阵乘 法的第四种形式里面见过它的作用。

如果存在一个 5x17 的矩阵 M，而其秩为 4， 那么它可以由 4 个秩 1 矩阵组合而成。

 

1，若矩阵空间 M 为所有的 5x17 矩阵，那么 M 中所有的秩 为4 矩阵所构成的集合 是一个子空间么？

答案是否定的，即使加入零矩阵也无法构成子空间，问题的关键是两个矩阵的加和，得到的矩阵的秩一定是4？两个矩阵之和的秩小于等于两个矩阵的秩之和。

2，若矩阵空间 M 为所有的 5x17 矩阵，那么 M 中所有的秩 为1矩阵所构成的集合 是一个子空间么？No, 

 

 所有v构成的S，它是空间？S包含0向量，并且对线性计算封闭，   所以它是空间，是R4的子空间。 

这个子空间的维数和基是什么？ 

它其实是矩阵A=[1,1,1,1] 的零空间，所以它的维数= n-r  = 4- 1 = 3  

它的基（给自由变量赋值0，1）可以是：

 

小世界图 Small world graphs

介绍小世界图主要是引出图论和线性代数的联系。

图是什么？

“图”是结点和边的集合：G=｛结点（nodes），边（edges）｝

 

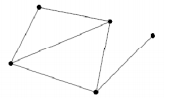
此图包含 5 个结点和 6 条边，我们完全可以利用一个 5x6 矩阵来完整描述它， 

我们可以用图来描述一个实际问题，如果每个人是一个结点，两个人互相认识 为一个边，那么整个美国可以以此构成一张大图。我们可以通过这张图来确认两个 人之间的最短距离是多少，即两个人需要通过最少几个朋友才能建立联系。G 本人 和克林顿之间的距离为 2，他的一个朋友是参议员，他认识这个参议员朋友，那个 人认识克林顿。班里的学生跟克林顿的距离因此不会大于 3。还可以继续算希拉里 和莱温斯基…… 所谓“六度分割理论”（six degrees of separation）猜想一个人和陌生人之间 间隔的点不会超过六个。因此当陌生的两人聊起这种联系都会感叹：“世界真小啊！” 这也是“小世界图”这个名字的由来。

图、网络、关联矩阵

图：

 

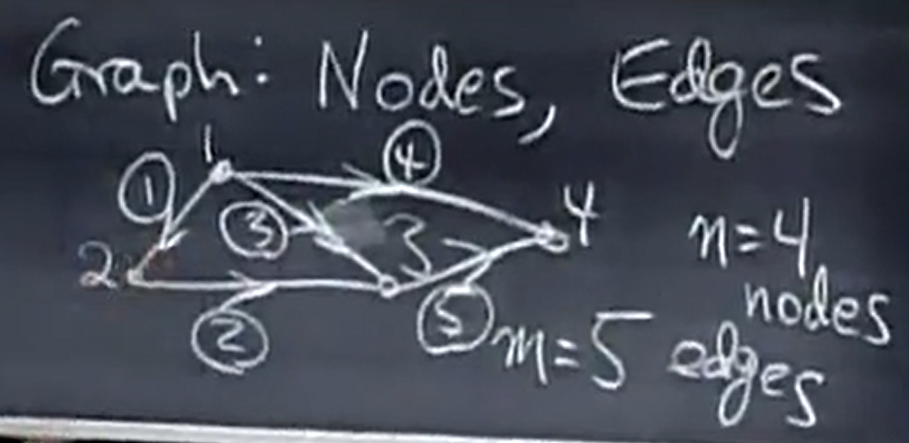
 构造一个矩阵来表示图的内在含义，此矩阵称为关联矩阵    

 

 

1,

 

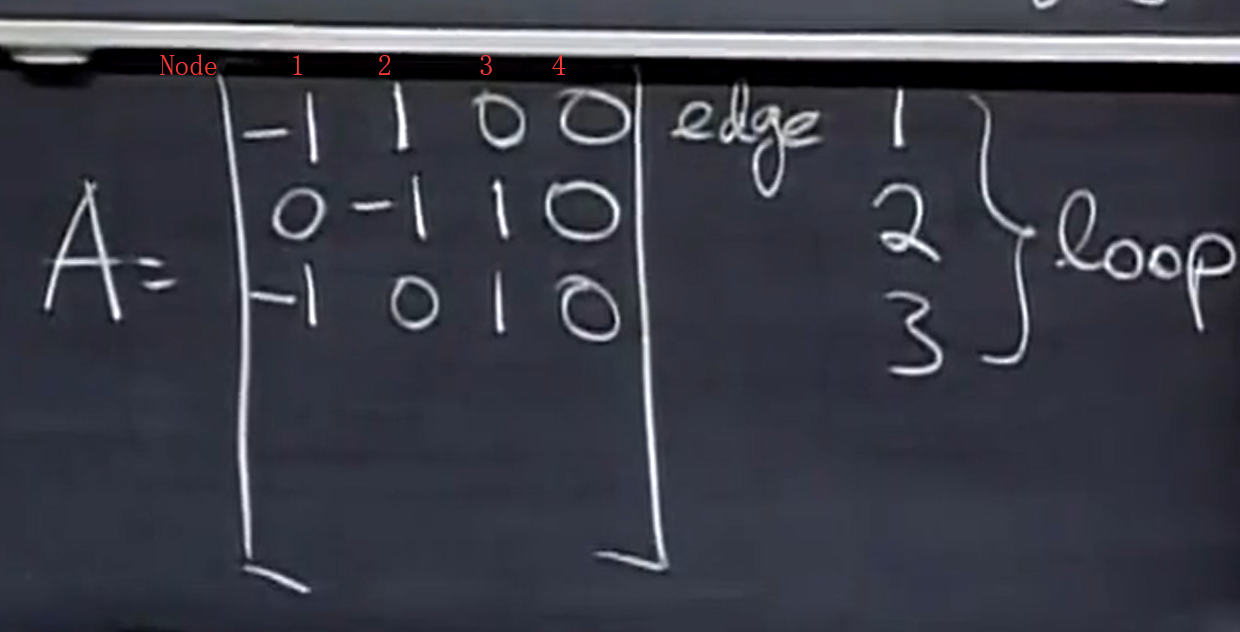
此时的三条边被称为一个loop , 

这将很自然的会提出问题，这三行相互独立吗？   当然不是，第一行加第二行就得到了第三行，

2,继续把这个图写完：

 

 

 

问题： 矩阵的零空间是什么？

当提及矩阵的零空间，我们希望了解的是什么呢？ 我们希望知道的是矩阵中的各列， 是线性相关还是线性无关，

如果各列线性无关，零空间就只有零向量。  

 

换言之，矩阵A的四列是线性相关还是线性无关？  

 

请注意矩阵A的实际意义， 通过矩阵A可以算出各边上的差值，

如果 x 为结点上的电势，则 Ax 给出了每个边上的电势差。

电势差什么时候全为0呢？全为0，也就是Ax=0 的零空间，

如果是所有的x 全为0，当然满足条件， 

这当然也满足条件，这是等电势，

 

请找出零空间的一组基，求解可以得到零空 间为一维 dim N(A)=1，所以一组基就可以是 x = [1,1,1,1] ， 零空间就可以表示为c[1,1,1,1]

这个零空间有什么物理意义吗？

说明等电势条件下不会有电流产生,c决定了所有结点电势上升或者下降，  

若求 Ax=b 的解，则相当于在给定了电压 b 的情况下，求各点的电势，但实际 上我们得不到电势的准确值，因为零空间有常数解 c，各点得到的电势需要加上常 数 c，这很类似于求积分要加上常函数，常数值需要边界条件来确定。

矩阵A的列数为 4，而其零空间的维数为 1，则矩阵的秩为 3，矩阵任意三列线性无关，矩阵第 1 列，第 2 列，第 3 列的列向量线性无关

 

考察矩阵的左零空间：

矩阵的左零空间是满足 ATy=0 的向量 y 的集合。因为矩阵 AT有 5 列，且矩阵 的秩为 3，因此矩阵的左零空间维数为 2   .   即（m-r）。这里的有可以理解为电流，对应于每个电势差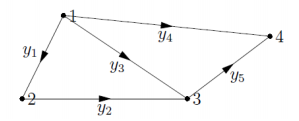

 

AT y = 0 的第一个方程是 -y1-y3-y4 = 0 。  这个方程对应于第一个结点，它说明了什么？它说明了合电流为0，

AT y = 0 的第二个方程是 y1-y2 = 0 。  这个方程对应于第二个结点，它说明了什么？它说明了y1= y2 ,流入2的电流和流出2的电流相同， 

AT y = 0 的第三个方程是 y2+y3 -y5 = 0 。  这个方程对应于第三个结点，它说明了什么？它说明 y2,y3 的流入和 y5的流出相同， 

AT y = 0 的第四个方程是 y4+y5 = 0 。  这个方程对应于第四个结点，它说明了什么？它说明 在结点4 ,y4和y5的总电流为0 

 

下面求出左零空间的一组基， （不用消元直接看图，从电路的角度去理解矩阵）

 

 

 

 

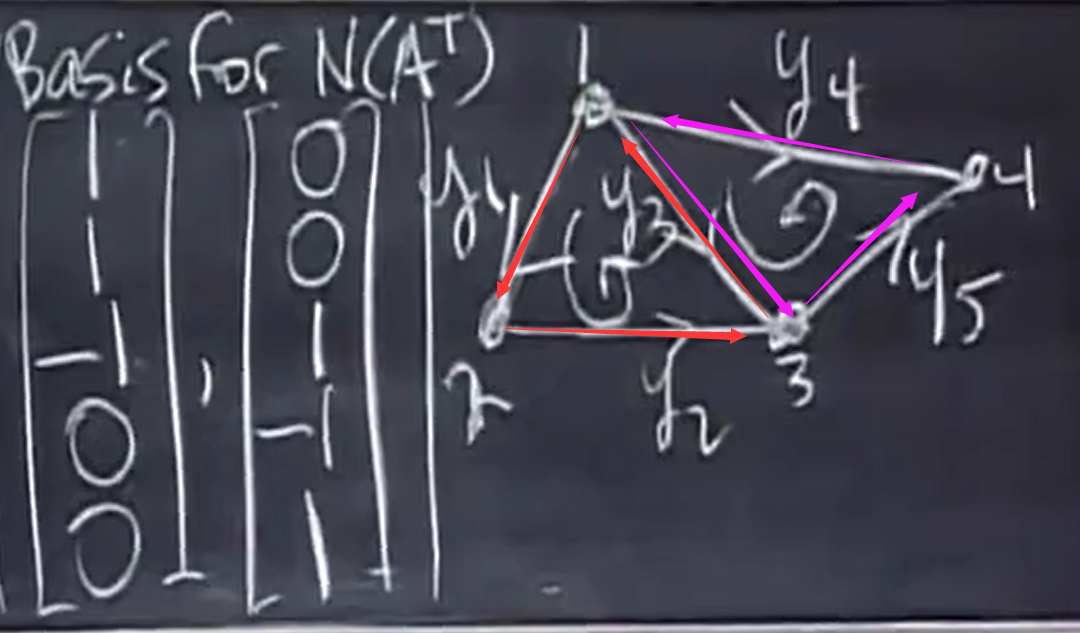
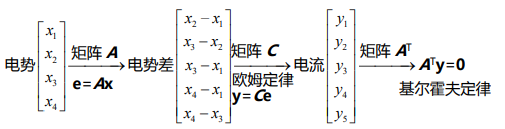
电势产生电势差，电势差产生电流，电流满足基尔霍夫定律的方程 （这些是在无电源的情况下的方程）

下面要将这三个方程联系起来， 

 

 

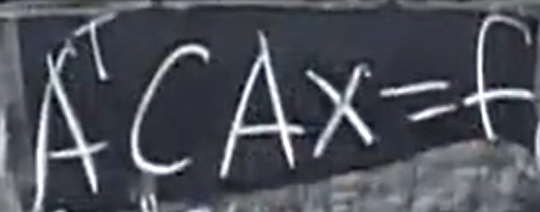
问： A的转置乘以A ,会得到什么？

得到的总是 对称的， 

 

 

考察矩阵的行空间：

矩阵的行空间的秩为3， 因为=r, 

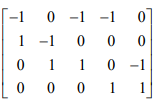
它有三个主列，分别是第一，第二，第四列，对应到图中是：

 

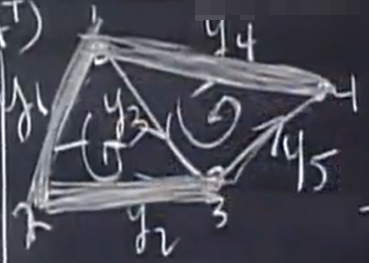
这三条边是没有回路的，线性无关对应到图中是没有回路， 

没有loop 的图被叫做树（Tree）， Tree = no loops, 

 

 

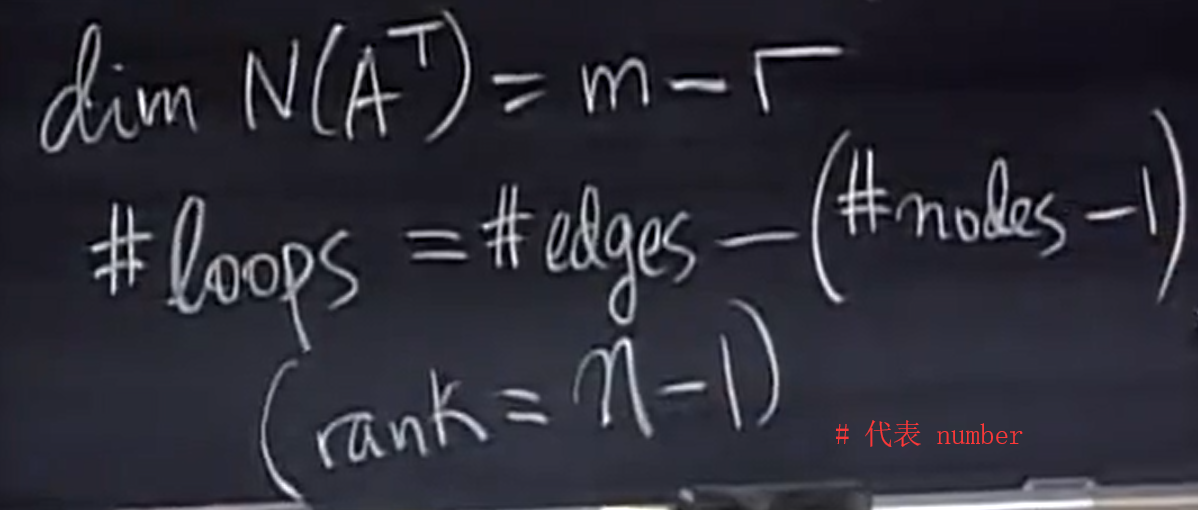
即：

 

这就是著名的欧拉公式，它对任何图都适用，这就用线性代数证明了欧拉公式， 

 

正交向量与正交子空间 Orthogonal vectors & subspaces

 

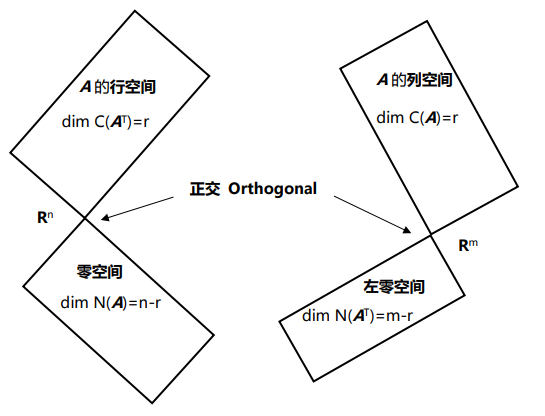
图中绘制空间成 90 度角，这是表示这两个空间正交。这张图是 GS 最得意的作 品之一，它反映了四个子空间的关系，在后面的课程中可以看到其两两形成正交补， 在 Rn空间中的向量会向两个子空间射影，并向 Rm空间形成映射，反之亦然。

正交向量 Orthogonal vectors

正交的向量如何判别？所谓的正交也就是垂直。

（默认的向量是列向量，x,y都是列向量表示）

当如下式子为零的时候是正交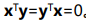，矩阵表示， 

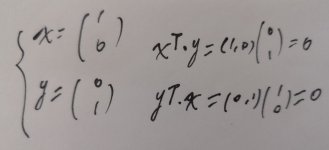一行乘一列的形式，  

 

推导正交向量要符合的条件：

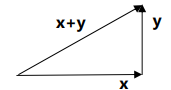
根据毕达哥拉斯定理，也就是我们常说的勾股定理，可知

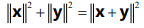，其中||   ||  表示的是向量的长度，

而且我们很容易知道，向量x的长度的平方等于x的转置乘上x,即，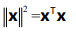

举个例子，向量（1,2,3）的长度的平方是多少？

 

 

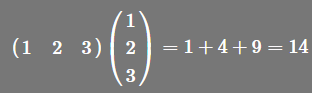
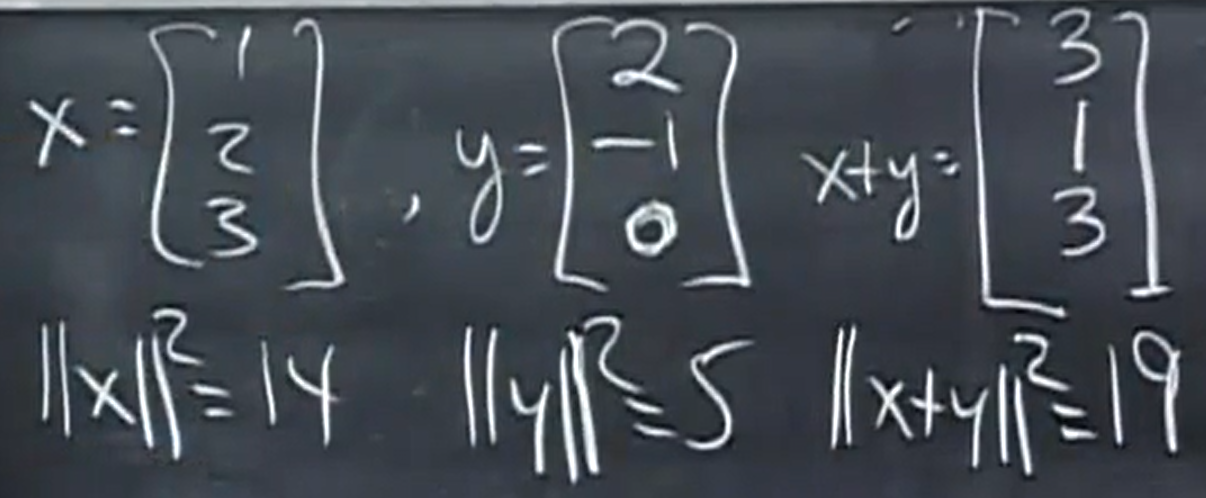
顺便问下，如果其中一个是零向量，那会怎么样？假设x是零向量，而y向量任意。它们是正交吗？Sure，当然，用零向量和任意的向量做点积，肯定结果总是零。所以我们得出结论，零向量与任意向量都正交。

讨论子空间正交：

如果我们说某个子空间与另一个子空间正交，那是什么意思呢？

我们定义子空间S与子空间T正交,我们有一对儿子空间，它俩相交是什么意思呢？这是个很自然推广，从正交向量推广到正交子空间。

S中的每一个向量都和T中的每个向量正交!

 

下面我们举个具体的正交子空间的例子：

一个黑板，它在三维空间里面是无限延伸的。它是一个子空间，一个平面，一个二维子空间。

一个地板，看做是另外一个子空间。

那么它们正交吗？它们是正交的吗？问题就是黑板上的每个向量都和地板上的每个向量正交吗？答案是不，它们不正交，我们很容易找到两个向量的点积不为零，举例来说，一个向量（yz平面）是（0,1,1），另外一个向量（x,y平面）是（1,-1,0），他们的点积就不为零。其实如果两个平面在某处会相交的话，那么他们一定不正交。

 

在R2 中，

什么时候过原点的直线会与整个平面正交？Nerver ,

什么时候过原点的直线与零向量正交？ Always 

什么时候过原点的直线与另一条过原点的直线正交？这种情况我们很了解，这两条直线的夹角必须得是90°。

现在我们知道了,两个子空间相交是什么意思？而这里想说的是，对于行空间和零空间也是如此，有如下结论，

1，行空间正交于零空间。

2，列空间正交于左零空间。

我们先看第一个结论，这是为什么呢？

首先，我们知道零空间指的是Ax=0的解所组成的空间，它为啥正交于A的行空间呢？

由这个式子我们可以得到如下等式,

 

所以这个等式告诉我们，x与A中所有的行都正交。

但是A的行空间可能不只是有A表面上的所有行，我们需要证明A的所有行空间的每个向量都和x所正交，那么A的行空间里还有什么呢？我们知道，A的行空间，除了这几行外还要包括他们的线性组合，所以其他的行空间的也很容易证明和x所正交！

 

现在我回过头来看这幅图，

我们其实是把一个空间划分为两个部分，这里是把n维空间划分为两个子空间（行空间和零空间），把m维空间划分为两个子空间（列空间和左零空间），

 

还有一件特别重要的事情。让我们看一下三维的空间的正交子空间是怎么样的。如果这些子空间不把整个空间分隔开，会发生什么样的情况？

例如，在三维空间里面，一组正交的直线，它们能够构成行空间和零空间吗？

也就是三维空间能出现行空间是一条直线，零空间是另外一条直线这种情况吗？不能，为什么呢？因为他们的维数不符合要求，1+1 不等于3。

这就是要补充的一件特别重要的事情,就是正交的两个子空间维数之和等于整个空间的维数。

此时称之为正交补（补集），这表明零空间包含所有（不只是部分）垂直于行空间的向量。

 

例子： ，此时A的行空间就是一条直线，这条直线通过点（1,2,5），此时A的行空间的维数是1，我们也很容易知道此时A的零空间的维数=n-r=2，所以A的零空间在三维空间里面就是一个平面，而且这个平面是垂直于向量（1,2,5）的一个平面。

因为在这里面2,4,10是不起作用的，所以我们可以对这个方程进行化简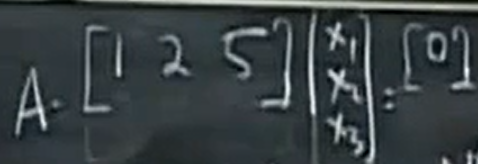，，它描述了一个平面，还有该平面的法向量。。

 

 

概括线性代数的内容

到目前为止，我想可以把线性代数的内容分为几部分

第一部分是线性代数的基本定理。这些基本定理表明了四个基本子空间之间的关系，第一部分的重点是研究维数，

第二部分在维数已知的情况下，重点研究它们的正交性。

第三部分将会是关于它们的基，也就是求所谓的正交基。

讨论如何求解一个无解方程组

也就是说，当Ax=b无解的时候，如何去解这个方程组？这种情况还是比较普遍的。这里的无解指的是b不在A的列空间里面,

举到现实生活中的例子就是，比如说要测量一个卫星到某地点的距离。我们可能需要测量1000次得到1000个方程，也就是说m等于1000，

但是，有的时候，我们并不需要需要那么多的方程，我们可能仅仅需要六七个就可以了。

所以意思就是说当方程数特别多的时候，等式的右侧(b)难免会混入“坏数据”，所以Ax=b 就无解了， 

我们甚至不知道我b中的哪一个数据有问题，不过这里还包含了许多“好数据”，包含了很多可以求出x的好数据。

所以我们需要做的就是要把这些坏数据给筛选出来。所以这正是线性代数需要解决的问题。如何去求解？这个最优解是什么？

 

下面通过代数的语言来描述这个问题，就是我们得到了一些方程，如何求出他们的最优解呢？

其中的一种方法就是不断去掉一些方程，直到剩下一个可逆的方阵，然后求出它的解。但是这个方法并不完美。因为对于所有测量值b而言，我们无法判断哪些是有效的好数据，而哪些是无效的坏数据。我们希望利用所有的测量值求出最优值,从而得到完整的信息。

那该怎么办呢？我们假设矩阵A是典型的长方形矩阵，也就是说m大于n。

这里面需要用到一个至关重要的矩阵。后面也会详细的介绍这个矩阵。这个矩阵就是,  

这是一个怎样的矩阵呢？

1，它是个方阵，nxn 的方阵（nxm  -  mxn   ->  nxn ）

2,它是个对称阵，

如何证明它是对称的呢？

 

所以，如何解决“不好”方程就是将原方程，改变为下面的方程：

 

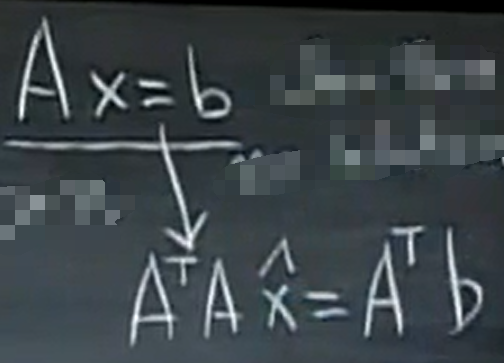
我们希望新的方程是可解的，

所以现在我们要了解这个重要的矩阵，它是否是可逆的？

下面举例： 

 

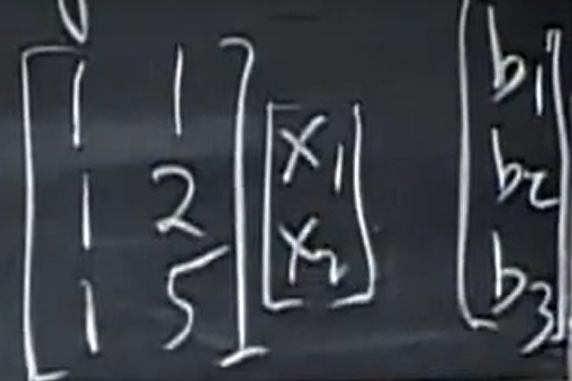
A是3x2 ,A的秩是2 ， 那么Ax=b 一定有解？ 

此时如果是想让方程有解的话，此时b必须在A的列空间里。但是呢，一般情况下是不会这么巧的。

所以此时要用到那个重要的矩阵，

 

就当前情况来说，它的确是可逆的，其实它不会总是可逆，

例如如果A是0矩阵（这是个极端的例子），

或者如下例子：它不可逆， 

其实，如果A的零空间只有零向量（A 的列向量线性无关），那么矩阵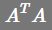可逆， 如何证明呢？

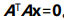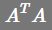假设存在x使得方程 如何证明可逆呢？

，

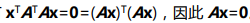所以，如果A的各列线性无关且，此时A的零空间只有零解，也就是方程只有零解，x=0 , 

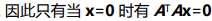，即该方程中的零空间只有零解，所以矩阵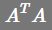的列向量也都是线性无关的，又因为它是方阵，所以可逆！

 

实际上：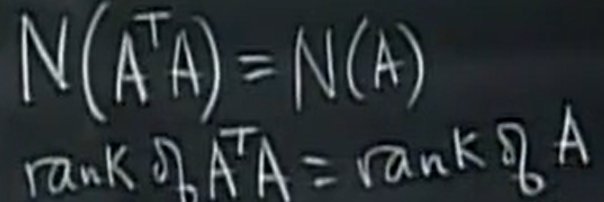

 

 

子空间投影 Projections onto subspaces

投影（射影）Projections

 

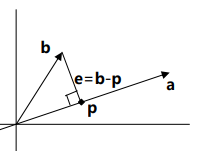
投影问题的几何解释就是：如何在向量 a 的方向上寻找与向量b距离最近的一 点。从图中可以看出，这个距离最近的点 p 就位于穿过 b 点并与向量 a 正交的直线 与向量 a 所在直线的交点上。这就是 b 在 a 上的投影。

因为 p 在向量 a 的方向上，因此可以令 p=xa，

所以，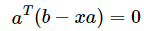

 

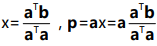
由 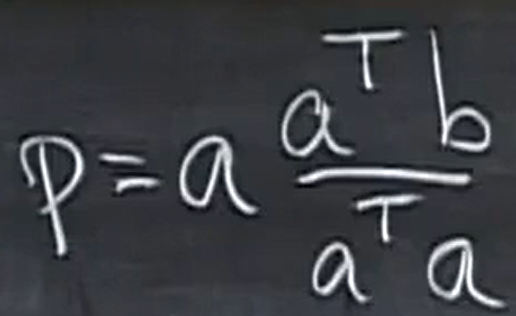，如果向量b变为原来的两倍，那么投影也会随之变为原来的两倍。

如果向量a变为原来的两倍，也就是说，被投影的向量翻倍的话会怎么样？答案是不会变，因为被投影的那条线没变。

投影我们可以理解为是由矩阵完成的，，P 指的是投影矩阵，  从公式里面我们很容易知道这个投影矩阵就是（其分子 T aa 是一个矩阵，而分母是一个数），如果此时的a向量是n维，那么投影矩阵P就是个nxn矩阵。

 

现在我们研究一下这个投影矩阵P的性质

这个矩阵的列空间是什么呢？

此时的列空间是通过a向量的一条直线， 因为此时的P是一列乘一行的形式（分母是个数字），所以列空间是通过a的一条直线，矩阵的秩为1。 

我们也很容易知道矩阵P是对称的矩阵，

另一方面，如果做两次投影则有 P^2b=Pb，这是因为 第二次投影还在原来的位置。

 

 

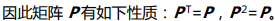
现在我们说一下为什么要做投影？

如前所述，方程 Ax=b 有可能无解，我们需要得到方程的“最优解”。这里的问题在于向量 Ax 一定在矩阵 A 的列空间之内，但是 b 不一定，因此我们希望将 b 投 影到 A 的列空间得到 p，将问题转化为求解 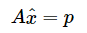, 不是那个不存在的x，而是那个最接近解的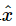

 

 

下面我们考虑一下高维的情况。这里不再是直线，而是一个平面，或者是三维，甚至是n维的子空间

 

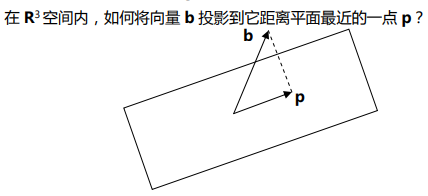
如果 a1和 a2构成了平面的一组基，则平面就是矩阵 A=[a1，a2]的列空间，

我们现在要做的就是求出向量b的投影。上图也表明了往往b不在矩阵A的列空间中,如果b在A的列空间中，那么b的投影结果就b自己。。

很容易知道向量 e = b - p 是垂直于这个平面的，

投影p是什么？投影p是基向量的组合，,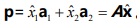   

所以 b -p 即b -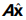 与这个平面垂直，   

可以得到如下两个方程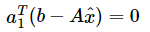：,，表示为矩阵形式如下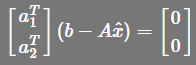：,即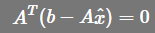，我们会发现平面上投影的方程和直线上投影的方程很相似。

 

 

既然我们对矩阵的四个子空间那么熟悉和不运用到这里呢？现在我们要问一下误差向量e,也就是在哪一个子空间里面？很明显，它是在矩阵A的左零空间里面。

而通过子空间的正交性，我们知道矩阵的列空间是正交于矩阵的左零空间的，所以现在我们知道误差向量e是垂直于A的列空间的。

下面开始解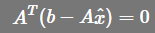这个方程，

 

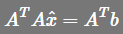
现在有三个问题, 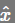   是什么？投影p是什么？投影矩阵P又是什么？

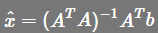
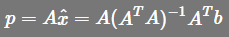
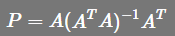,此时不可以随便化简为 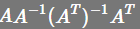，这时P就是单位矩阵了，此时只有当A是方阵且可逆的时候才会成立，（而一般A都不是方阵）。举例说明A为方阵的时候，P就是单位矩阵，如果A是3x3的可逆方阵，那么A的列空间就是整个3维空间，我们要对整个3维空间投影，那么投影矩阵显然是单位矩阵， 

 

容易知道：

,

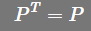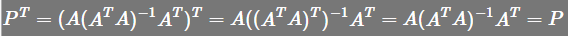
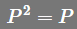,从几何学的角度来说，第一次将投影投到列空间，第二次将投影投到列空间都是一样的, 证明如下：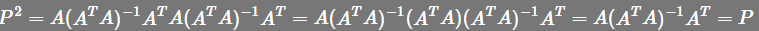

 

实际应用 ---- 最小二乘 Least Squares

 

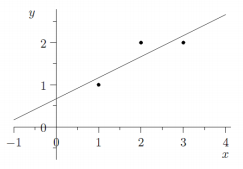
应用投影矩阵求方程组最优解的方法，最常用于“最小二乘法”拟合曲线。 有三个数据点{(1,1), (2,2), (3,2)}，求直线方程 y=C+Dx，要求直线尽量接近于 三个点。把三个点的数据代入方程则有：

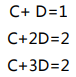
矩阵形式如下：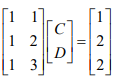

这个的方程 Ax=b 是无解的，解决办法就是求其最优解，即方程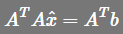 的解，  

具体拟合如下：

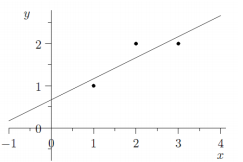
还可以从误差最小的角度出发求解：

 

投影矩阵

 

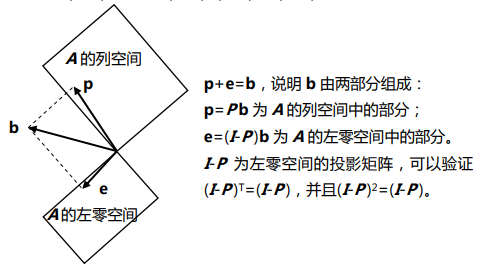
可以验证，向量 p 与 e 正交，并且 e 与矩阵 A 的列空间正交,   

 

 

 

 

又如：

 

 

正交矩阵和施密特正交化 Orthogonal matrices & Gram-Schmidt

本讲我们完成对“正交”的介绍。Gram-Schmidt 过程可以将原空间的一组基 转变为标准正交基。

 

标准正交向量  Normal Orthonormal vectors

 

换而言之，它们都具有单位长度 1（这正是Normal 所在），并且彼此正交。很多线性代数的计算都建立在标准正交基础上，它让一切变得简单可控。  

标准正交矩阵 Orthonormal matrix

 

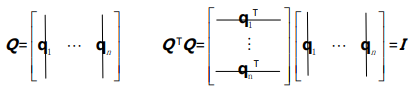
注意这里的矩阵 Q 可以不是方阵。

 

一个 标准  正交 的方阵我们称之为标准正交矩阵

注意必须是方阵，必须是标准正交，而不只 是正交。  

此时，，也就是Q矩阵的转置等于Q的逆，

 

举例：

 

注：一般所说的正交矩阵也是指的是标准正交矩阵。 

那么 ，标准正交矩阵的好处是什么？

它方便了什么计算，

 

在很多复杂问题中使用标准正交向量之后都变得简单，

如果A是正交矩阵（没说方阵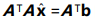），，求解将不用再求逆了，直接

, 

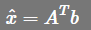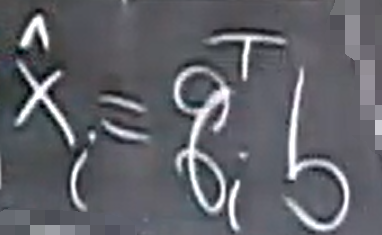  这个式子在很重要， (q是A的列向量）

施密特正交化 Gram-Schmidt

现在我们的目标是让矩阵正交化，使列向量标准正交。

我们以下面的例子开始，

假设有两个向量，a和b(线性无关)，如下图所示：

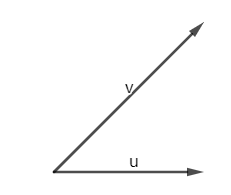
我们想要正交化这两个向量,   注：它们可能是在二维空间，也可能是在12维空间。

对于如何正交化这两个向量,Graham 和 Schmidt 提供了方法，

 

 

 

 

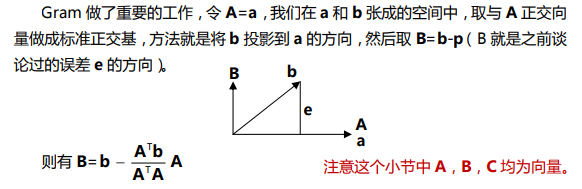
下面考虑A矩阵（不是上面ABC的向量） 和 矩阵Q的关系：

 

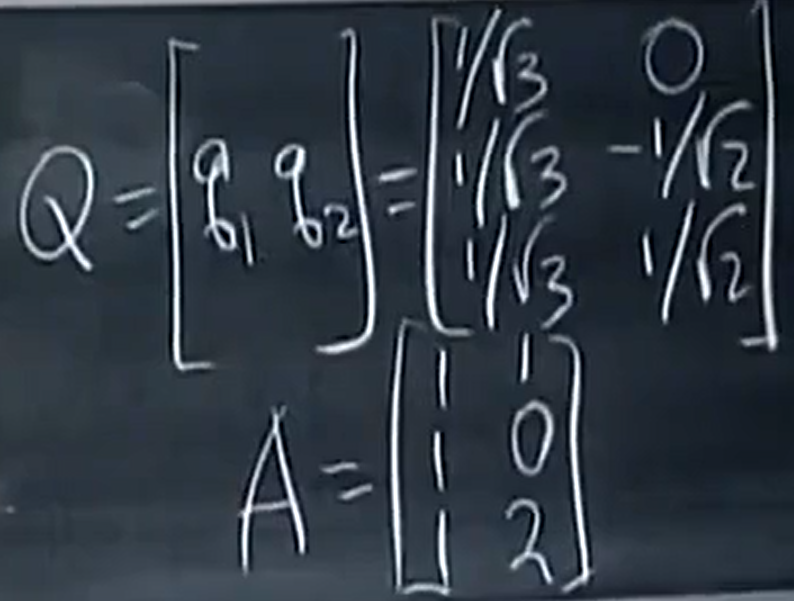
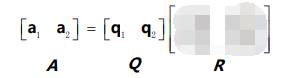
1， R应该怎么写呢？

 

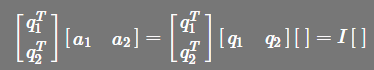
所以，R=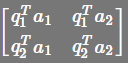 

2，为什么R是上三角阵？

这是因为a1 和 q1 方向相同，   这是因为 a1就是 q1的方向，而 q1和 q2为标准 正交向量，因此 q2的方向与 a1垂直，因此内积为 0，所以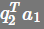=0

 

 

总结： 

 

 

 R 在 Q 右侧相当于对 Q 做列 操作，即 A 的列向量是 Q 列向量的线性组合，而 Q 为 A 列空间的一组标准正交基， 则 R 的元素实际上是 A 的列向量基于 Q 这组标准正交基的权。

采用矩阵的 QR 分解来帮助求解 Ax=b 的问题，最大的优势是提高了数值的稳定性,

行列式及其性质 Properties of determinants

迄今为止，我们已经学习了很多关于长方矩形的知识，现在我们把注意力转向方阵 。

行列式 Determinants 

行列式是一个每个方阵都具有的数值，我们将矩阵 A 的行列式记作 det(A)= A 。 它将尽可能多的矩阵信息压缩在这一个数里。例如 矩阵不可逆或称奇异与矩阵的行列式等于 0   等价，因此可以用行列式来判定矩阵是否可逆。

 

行列式的性质 Properties

直接给出 n 阶行列式的公式，则一下子代入了大量信息，并不利于接受这个概 念，我们从行列式的三个性质开始讲起，这三个性质定义了行列式

注意：3b 的意思不是 det (A+B ) = det(A) +det(B). 这里的线性组合只能单独在一行上！ 

行列式的性质 2 中隐藏着一个内容，这就是置换隐藏着奇偶性，一个矩阵不可能经过奇数次置换（交换）得到和偶数次置换相同的矩阵。

 

 

更多的性质可以从以上的三条性质中推导出来：

4. 如果矩阵的两行是完全相同的，则它的行列式为 0。这可以从第二条性质推导 出来，因为交换这个相同的两行，行列式应该变号；但是新生成的矩阵跟原矩 阵没有区别，因此行列式应该不变，所以有 det=-det，所以 det 等于 0。

5. 从矩阵的某行 k 减去另一行 i 的倍数，并不改变行列式的数值，

我们以二阶为例：

 

6. 如矩阵 A 的某一行都是 0，则其行列式为 0。可以应用性质 3(a)，取 t=0 证明。

7. 三角阵的行列式的值等于其对角线上数值（主元）的乘积。

 

 

8. 当且仅当矩阵 A 为奇异矩阵时，其行列式为 0。

如果矩阵 A 为奇异阵，则必可通过消元法使得矩阵的某行全等于零，则按照性质 6，A 的行列式为 0。

如果其不是奇异阵，则通过消元可以得到一个上三角矩阵，且其主元均不为 0， 则按照性质 7，行列式的数值等于主元的乘积也不等于 0。

计算非奇异矩阵的行列式有确切的公式，但通常计算机（例如Matlab）是靠消元的方法来转化为三角阵，然后将主元相乘来进行计算的。

 

前八个都是关于行列式自身的性质

9. det(AB)=det(A)det(B)

尽管矩阵的和的行列式不等于行列式的和，但矩阵乘积的行列式等于矩阵行列式的乘积。

推论：

此时A是 nxn  !

 

最后一个公式让我们容易联 想到体积，当长宽高都倍增之后，体积变成了原来的 23=8 倍

 

10. det(A T)=det(A)

 

 

行列式公式和代数余子式 Determinant formulas and cofactors

我们已经认识到了行列式的性质，应该推导出其公式了，

行列式公式 Formula for the determinant

我们知道行列式有如下三个性质：

1. det(I )=1。

2. 如果交换行列式的两行，则行列式的数值会反号。

3. 行列式是“矩阵的行”的线性函数。 从这三条性质可以推导出后续的七条性质，从这十个性质出发可以得到二阶方 阵的行列式公式：

 

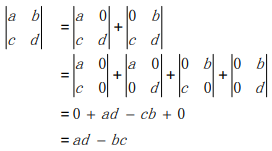
通过性质 3 对 n 阶矩阵的行列式进行拆分，我们可以得到所有只包含 n 个非零元素的行列式，对于二阶行列式我们从 1 个拆分为 2 个，然后拆分成 4 个。而对于 三阶矩阵我们从 1 个拆分成 3 个，然后拆分成 9 个，最后要拆分成 27 个。但最终这些行列式中有很大一部分等于 0。

 

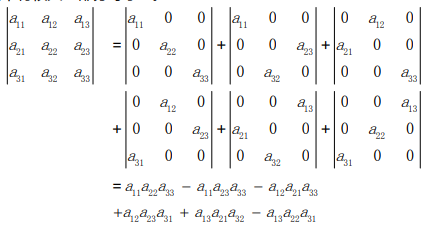
每一个拆分出来的非 0 行列式都是在每行都有且只有一个元素，就如同置换矩阵的元素分布。应用性质 3 可以将元素从行列式中提出来，

而置换矩阵的行列式值为+1 或者-1，因此可以给出行列式的公式。

n 阶矩阵拆分为非 0 行列式的个数  的计算方法就如同计算置换矩阵的个数一样，第一行放置一个非 0 元素的位置有 n 个 选择，第二行为 n-1 个……1个。最后得到共 n！个矩阵。

对于拆分得到的三阶矩阵，元素从上至下朝向右侧方向的，其行列式的数值为 正，朝向左侧方向的则为负。但是这个规律只适用于三阶矩阵，不适用于高阶矩阵。

 

 

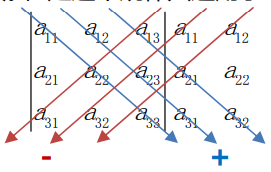
现在要总结一个适用于n阶的行列式的去求法：

 

 

元素aij 的代数余子式 Cofactor formula

代数余子式是用较小的矩阵的行列式来写出 n 阶行列式的公式,它是从归纳出来的，

 

 

 

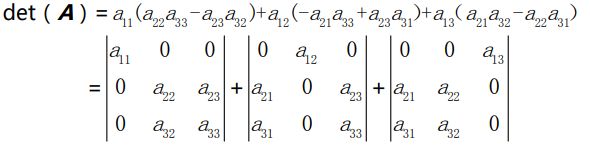
所以，对于n阶方阵，我们沿第1行展开，

 

对于矩阵行列式的计算，消元的得到主元是一个很好的方法，与之相比行列式的展开公式较为复杂，

而代数余子式的方法介于两者之间，它的核心想法是通过降阶来将原来的行列式展开成更简单的行列式。

 

举个  三对角阵（tridiagonal matrix）为例，它除了对角线和对角线两侧相邻的元 素之外，其它元素均为 0。

如何求An ? 

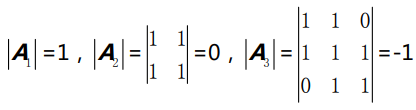
例如求A4,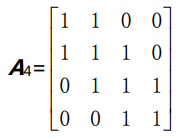

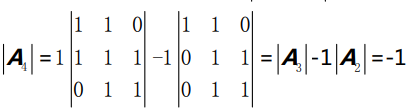
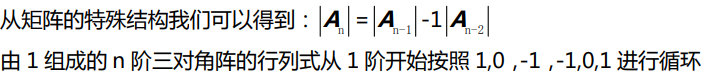
逆矩阵、克莱姆法则、体积  inverse matrix,Cramer’s rule,and volume

我们已经了解了行列式的公式和性质，下面讨论它的应用

求逆矩阵的公式 Formula for A−1

我们容易知道二阶矩阵的逆矩阵公式：

 

那么我们能写出三阶甚至高阶的公式么？通过观察二阶矩阵逆矩阵的公式，我 们可以用同样的策略来构造高阶矩阵的求逆公式，为

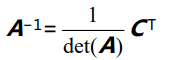
 而矩阵C是“代数余子式矩阵”（cofactor matrix）C 的转置矩阵 C^T。即伴随矩阵（adjoint matrix）。

 

下面我们要证明这个式子成立：

等价于如下式子成立：

 

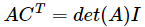
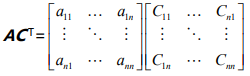
根据公式，一行中对应的元素乘以它对应的代数余子式 之和 为det (A), 

所以 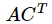对角线上的值都是 det(A), 

现在只差一步，就是其他的值为什么都是0 ，例如 A的第一行和 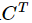的第二列，为什么是0？

其实就是说，如果元素是来自行列式的某一行，而代数余子式并不是该行，这时得到的结果为0，why?

 

 

所以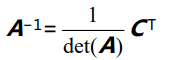， ，所以这就是矩阵的求逆公式，

 

克莱姆法则 Cramer’s Rule for x = A^(-1)b  

现在我们已经知道了 A的求逆公式，那么 对于Ax = b ,那么

 

所谓的克莱姆法则就是在上面这个式子的基础上有稍稍近了一小步而已，

克莱姆法则是从另一个角度来看待这个公式，

 

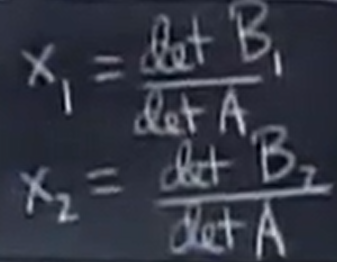
现在就是B1 是什么？其实这个矩阵B就是，矩阵 B为用向量 b 替换矩阵 A 的第 j 列所得到的新矩阵。  

 

 

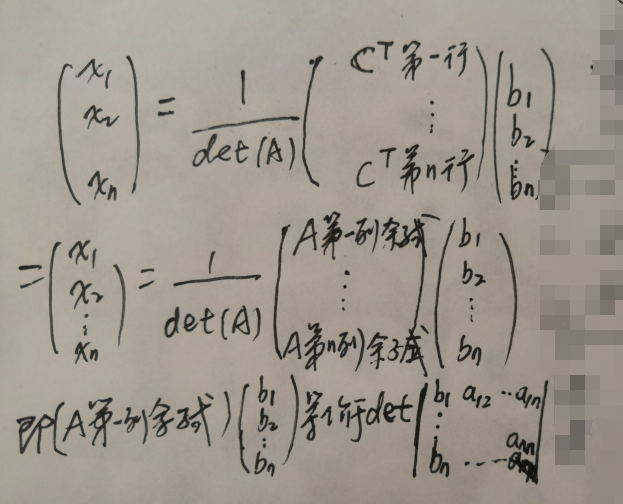
这就是克拉姆法则，   

 

但是，克莱姆法则看似简单，但是却不是省油的灯，

相比于消元法，采用克莱姆法则计算方程的解效率较低，因为克拉姆法则，必须要计算出n+1 的行列式的值，n个B，1个A，   

所以，虽然公式很漂亮但是不建议使用它们来计算Ax=b , 中看不中用，我们有更使用的方法，正如Matlab 一样（通过消元求解），

通过行列式来求体积

矩阵 A 行列式的绝对值等于以矩阵 A 行（列）向量为边所构成的平行六面体的体积。行列式的正负对应左手系和右手系。

之前提到过行列式是将矩阵的信息压缩 成一个数，可以将“体积”视为它压缩后给出的信息。 

 

 

如果矩阵 A 是单位矩阵，则其构成的是三个边长均为 1 且互相垂直的立方体， 其体积为 1，这与上面的结论相符。这也是行列式的性质 1

 

 

而如果矩阵 A 为正交矩阵 Q，则其构成的也是三个边边长为 1 且三边互相垂直 的立方体，其体积也为 1 只是取向与单位阵不同，

问：为什么Q的行列式=1或-1？因为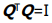，对方程两边同时求行列式得：根据性质9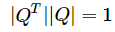，,又根据性质10，得。  

 

 

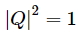而如果矩阵 A 构成的是长方体，也非常直观，当你将其中一条边的边长增加 2 倍时，正方体的体 积也会增加 2 倍成为长方体，这满足行列式的性质3a, 

 

到目前为止，已经满足了行列式的性质1,2,3a,下面看下3b,

如何求平行四边形的面积？

 

结果可以推广到高纬，  

例子：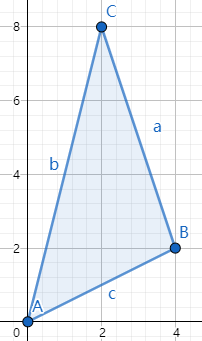 

 

三角形的面积:

 

 

 

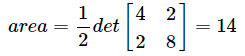
特征值和特征向量 Eigenvalues and eigenvectors

本单元后面的课程主要围绕特征值和特征向量。在这个议题下讨论的都是方阵。

特征向量和特征值

将矩阵 A 与向量 x 相乘当做是对向量的一种操作或者函数输入 x 而输出 Ax。

我们知道大多数的Ax 都是不同方向，不平行与输入的x的，但是有特定的A能使得Ax平行于输入的x ,这时的x就是矩阵A的特征向量。 

 

 

问：如果 0 是矩阵的特征值，特征向量是什么？

即Ax=0,所以特征向量是A的零空间的向量，  

问：如果 矩阵不可逆，即是个奇异矩阵，特征值包含0？

包含，因为A 不可逆，所以 Ax = 0， A的零空间不仅仅有零解，设x1 不是Ax=0 的零解，所以Ax1 = 0  x1  ，所以此时0是特征值，x1是特征向量。 

 

但是现在我们想要的是求出所有的特征值和特征向量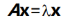，  有两个未知数， 

 

这需要好的方法去求解，先看两个例子，

例1：矩阵 P 是朝向某平面的投影矩阵，

 

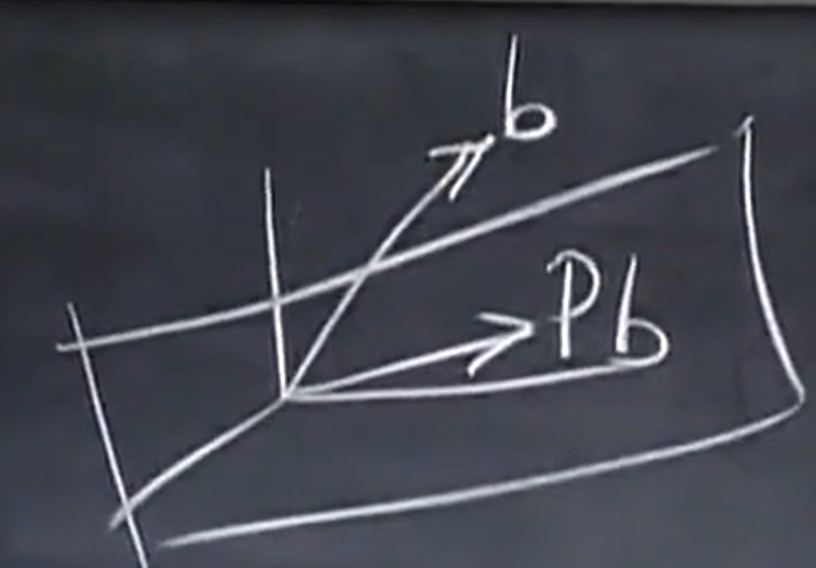
对于这个平面之内的 x，均有 P x=x， 因此 x 是特征向量而 1 为特征值。

垂直于该平面的向量 x 经投影得到 P x=0， 这个 x 也是矩阵的特征向量而 0 为特征值。

所以这个矩阵的特征值就是1和0，  

提前说一个特征值的性质，  nxn 矩阵有n个特征值，  特征值的和= 对角线的元素之和，这个和数叫做迹！  

 

如何求解Ax = λx

回过头来，如何求出所有的特征值和特征向量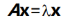，  ,此时方程有两个未知数， 

方程 Ax=λx 中特征值和特征向量均未知，没法直接求解。因此我们做如下处理：Ax=λx，

因此有（A-λI）x=0，  此时如果不想只有零解，则 A-λI 应该是奇异的矩阵， 所以 det (  A-λI ) =0 . 

这时问题就由 Ax = λx 转换到    det (  A-λI ) =0  了，  就只剩一个λ 了，这个关键的方程，叫做特征方程，或者说特征值方程，  

 

举个例子：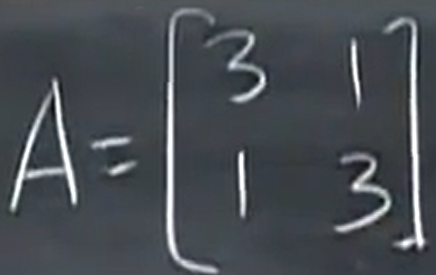

 

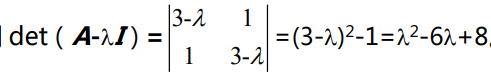
可以看到其中的参数 6 是矩阵 A 的迹而 8 是行列式的值 ， 

通常一个 2 阶矩阵的特征值 是如下方程的解，，

 

对于上述矩阵 A，可以求得特征值λ1=4    和    λ2=2  ，

下面就要根据特征值求出对应的特征向量了， 

这个例子与例2中矩阵 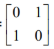的特征值和特征向量相对比，在例2 的基础上加了3I （单位矩阵）。

从例2到这个例子，特征值增加了3，特征向量没有变， 

 

来看下为什么？

如果Ax = λx ,

那么现在在A上加上3I， （A+3I)x就是等于 Ax+3Ix =  λx + 3x =  （ λ + 3）x, 

所以就是特征值增加了3，特征向量没变，  

需要注意的是，两个矩阵的和的特征值不是两特征值直接相加之和，因为特征向量可能并不相同， 

 

复数特征值

关于旋转矩阵，我们假设是将一个向量（x,y）旋转90度， 

 

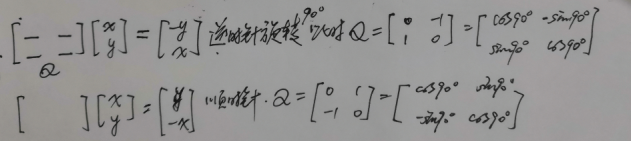
一般情况都是逆时针旋转的，所以对于二维的向量，更一般的旋转矩阵为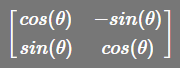

对于三维来说：

绕x轴旋转：

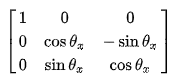
绕y轴旋转：

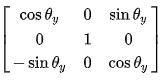
绕z轴旋转：

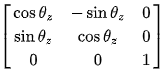
上面扯得有点远了，只是因为编程中有时会用到旋转矩阵，

 

继续：

 

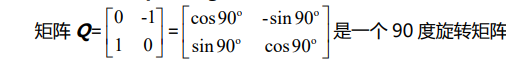
三角阵和重特征值

上面出现了复数特征值，有点糟糕，但还不是最糟糕的，下面看更糟糕的，

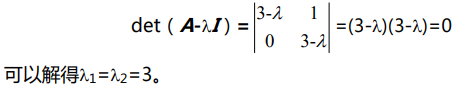
为什么我们认为这个矩阵更糟糕，因为它们会得到两个相同的特征向量，

 

对角化和矩阵的幂 Diagonalization and powers of A

本讲中将学习如何对角化含有 n 个线性无关特征向量的矩阵，以及对角化是怎样简化计算的

对角化矩阵 S^-1AS = Λ

 

这里的 Λ 也称作特征值矩阵， 

对于消元法而言，矩阵有 LU 分解，对于施密特正交法，矩阵有 QR 分解，而 上面的推导（A=SΛ S^-1）是一种新的矩阵分解。

 

矩阵的幂 Powers of A

 

 

重特征值 Repeated eigenvalues

如果矩阵 A 没有重特征值，则其一定具有 n 个线性无关的特征向量.

如果矩阵 A 有重特征值，它有可能具有 n 个线性无关的特征向量，也可能没有。

比如单位阵的特征值为重特征值 1，但是其具有 n 个线性无关的特征向量。  

 

所以，即使一些矩阵无法对角化处理，但是大部分矩阵都是可以的， 如果特征值都不相同就可以对角化（这也是绝大多数的情况）。 

差分方程

 

所以： 

斐波那契数列

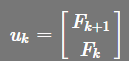
则有：

（这就将二阶标量差分方程  变为了一阶向量差分 方程了）

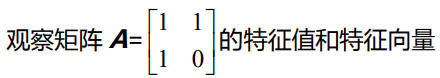，，因为其为对称矩阵，特征值为实数， 且特征向量正交。

（u0 写为 特征向量的  线性组合  ）

 

Note： 对称矩阵的特征值 和 特征向量的性质，它的特征值一定是实数，不会是复数，它们的正交向量也一定是正交的！  

微分方程和 e^(At)

这部分我们要讲  如何解一阶方程，

本讲中我们将面对微分方程，将一阶常系数微分方程转化为线性代数问题进行处理。

主要思路基于常系数线性方程的解是指数形式，而寻找其指数和系数就是线代主要研究的问题。这里会涉及到矩阵型指数的运算  e^(At)

 

微分方程 Differential equations

 

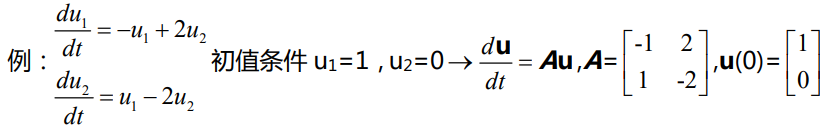
分析矩阵 A 的目的是要追踪 u 随时间的变化，而首先要做的是找到矩阵的特征 值和特征变量。

因为矩阵 A 为奇异矩阵，因此存在一个特征值λ1=0，而矩阵的迹为-3， 因此还有一个特征值λ2=-3 。  

 

特征向量给出的是方向，

c 给出的是在不同方向上所占权重，

而特征值给出的 是矩阵操作在特征向量方向的操作效果，

在上一讲差分方程里它就是一个倍数即线 性增长能力，而在微分方程中它代表在该方向上的指数增长能力。因此两者稳定性 的评价并不相同。  

 

省略...   太难了 暂时不听了

马尔可夫矩阵，傅里叶级数

本讲学习马尔可夫矩阵和傅里叶级数，两者是关于特征值和投影矩阵的应用，

马尔可夫矩阵 Markov matrices

 

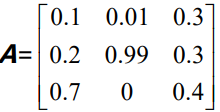
形如矩阵 A，

1，任何元素非负，

2，且每列的元素加和为 1

的矩阵被称为马尔可夫矩 阵。

马尔可夫矩阵主要应用在概率领域。将一个马尔可夫矩阵进行方幂运算得到的 仍旧是马尔可夫矩阵。

 

 

为什么每一列的元素加和为 1 这个条件，保证了矩阵具有 1 这个特征值？

 

所以 A- I 肯定有0这个特征值， 所以A肯定有1这个特征值，  

 

省略...   太难了 暂时不听了