现代计算机都是使用补码的编码方式 来表示有符号整数

 

三种编码方式：

例1：

这里假定w=4（4位）,

机器中能表示的所有情况：

0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111  总共有16中表示方法，

第一种方法（补码）：B2T（现代计算机都是使用这种方式表示有符号整数）

0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 

   0        1     2       3        4     5        6      7        -8      -7      -6     -5       -4    -3       -2     -1  

第二种方法（反码）：B2O

0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111  

  +0        1     2       3        4     5        6      7       -7     -6     -5       -4    -3       -2     -1     -0  

第三种方法（原码）：B2S

0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111  

  +0      1     2       3        4        5      6        7      -0      -1     -2     -3       -4    -5       -6     -7 

 

这就是三种编码方式的区别！（本质就是上面的三个公式！）

 

例2：

这里使用第一种编码方式（补码），

w = 4 （这时的取值范围是 -8 ~ 7 ）

因为我们采用了第一种编码方式，所以，0101 表示5！ 

假设x = 5, 如何得到 - 5 的二进制表示呢？

可以采用下面的方法：首先使用公式, 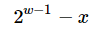 得到一个正数，这里是3（8-5=3）, 

则-5 的二进制表示就是 3的二进制表示，不过要将3的二进制的最高位变为 1 (0011   --> 1011)！ 

即-5 的二进制表示是：  1011 

 

练习：

采用第一种编码方式，w = 8 

-106 的二进制表示 = 1001 0110 。 首先是 128 - 106 = 22 ，22 的二进制表示为 0001 0110 ，所以为 1001 0110！ 

 

例3（现代计算机都不采用这种编码方式，仅练习）：

这里使用第二种编码方式（反码），

w = 4 （这时的取值范围是 -7 ~-0 ~+0 ~7 ）

因为我们采用了第二种编码方式，所以，0101 表示5！ 

如何得到 - 5 的二进制表示呢？

可以采用下面的方法：使用公式,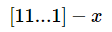  

1111 - 0101  = 1011 

即-5 的二进制表示是：  1011 

 

练习：

采用第二种编码方式，w = 8 

-106 的二进制表示 = 1001 0110 。 首先106 的二进制表示为 0110 1010 ，所以为 1001 0101！