线性排序算法

前言

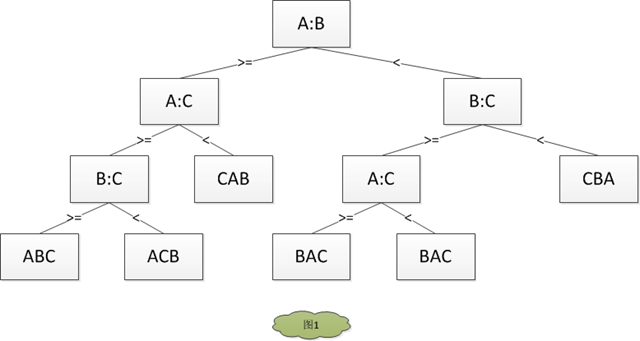
插入，快速，合并，堆排序等基于比较的排序算法的最坏情况下界为Ω(nlogn)，最坏情况下都要进行Ω(nlogn)次比较。假设有一n个元素组成的数组（假设每个元素都不相等），那么一共有n!排列组合，而且这n!排列组合结果都应该在决策树的叶子节点上（如图1），在图1中n = 3，所以有3! = 6种组合全都在决策树的叶子节点，对于高度为h的二叉树，叶子节点的个数最多为2^h (当为满二叉树时为2^h,这里根节点为第0层)。所以n! <= 2^h ,从而h >= log(n!)  = Ω(nlogn)。证明如下

 

线性排序算法

计数排序

假设：有n个数的集合，而且n个数的范围都在0~k(k = O(n))之间。

运行时间：Θ(n+k)

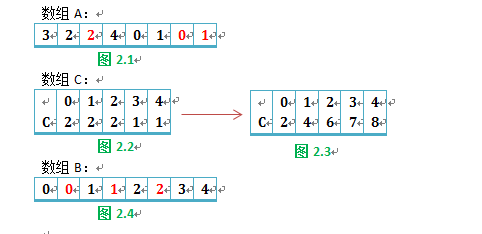
待排序数组A如图2.1所示，需要辅助数组B(存储最后排序结果)，数组C(存储元素的个数)。基于上述的假设，数组C的大小为k，C[i]表示数组A中元素i(0 <= i < k)的个数(如图2.2所示)，为了保证计数排序的稳定性，数组C变化为图2.3，C[i]表示小于或者等于i的个数。代码如下：

/*
    输入：待排序数组A,存储排序后的数组B，数组A的大小，数组C的大小
    功能：计数排序
*/
void CountingSort(int A[], int B[], int len, int k)
{
    int *CountArr = new int[k];
    int i;
    for (i = 0; i < k; i++)
    {
        CountArr[i] = 0;
    }

    for (i = 0; i < len; i++)
    {
        CountArr[A[i]]++;
    }

    for (i = 1; i < k; i++)
    {
        CountArr[i] += CountArr[i-1];
    }

    // 从右至左保证算法的稳定性
    for (i = len-1; i >=0; i--)
    {
        B[CountArr[A[i]]-1] = A[i];
        CountArr[A[i]]--;
    }
}

9-12行和19-22行的运行时间Θ(k)，14-17行和25-29行的运行时间为Θ(n)，所以总的运行时间为Θ(2(n+k)) = Θ(n+k)。

基数排序

基数排序：将所有待比较数值(正整数)统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后， 数列就变成一个有序序列。

基数排序分为两种LSD和MSD。

LSD(Least significant digital)：最低有效位优先，即从右向左开始排序。

MSD(Most significant digital)：最高有效位优先，即从左往右开始排序。

以下是LSD方式的基数排序的伪代码

RadixSort(A,d)
    for i <- 1 to d
        用稳定的排序算法排列数组A中元素的第i位

如图3：先牌个位，然后十位，最后百位。为数组的某一位排序的时候一定需要稳定的算法。

运行时间为Θ(d(n+k))。在基数排序中排列数组各位的算法是计数排序所以运行时间为Θ(n+k)，又d是数组中数的最大位数。

桶排序

桶排序：将数组分到有限个桶子内，然后再对桶子里面的序列进行排序，运行时间Θ(n)。桶排序基于一个假设：输入的数据由随机过程构成，否则在最坏情况下都分配到一个桶子里面，如果又不满足计数排序的假设要求，那么只能使用基于比较的排序算法进行排序，运行时间就退化到Ω(nlogn)。

排序算法稳定性

排序算法稳定性：假设待排序序列中有两个元素相等，而且在排序前和排序后两个相等的元素的相对位置不变，即有 a = b，排序前a在b前面，那么排序后，a还是要在b前面。排序算法的稳定性是要看具体的算法实现，比如一般情况下，直接选择排序，快速排序，希尔排序，堆排序都不是稳定排序算法，基数排序，计数排序，归并排序，插入排序，冒泡排序都是稳定排序算法。

快速排序：A = {2， 2， 1}，排序后A = {1，2，2}。

希尔排序：A = {1，2，5，4，4，7}，排序后（k = 2）；A = {1， 2， 4， 4， 5， 7} 。

堆排序：A = {2，2，1}，排序后A = {1，2， 2}。

直接选择排序： A = {4， 4， 2， 5},排序后 A = {2，4， 4， 5}。

以上举例都不满足稳定性。