神秘题目2
签到题
这很不签到 \({\color{White}{cjz:这水题本神仙1秒切10道}}\)
题目描述
给定一颗 \(n\) 个节点的无根树,每个节点有一个权值 \(a_i\) ,你需要选一个起点 \(S\) ,从这个节点开始深度优先遍历,得到一个 dfs 序:\(x_1=S,x_2,x_3...x_n\) 。
你需要最小化 \(\sum\limits_{i=1}^n i\times a_{x_i}\)。
输入格式
第一行一个整数,\(n\) 表示节点数。
接下来 \(n-1\) 行,每行两个整数表示一条边。
接下来一行 \(n\) 个数,表示 \(a_i\) 。
输出格式
一行一个整数,表示答案
输入样例
5
1 2
1 3
3 4
3 5
5 4 3 2 1
输出样例
35
数据规模与约定
对于 \(30\%\) 的数据,\(n\le 1000\) 。
对于 \(100\%\) 的数据,\(1\le n,a_i\le2\times10^5\) 。
题解
分析
算法:显然树形dp。
用脚思考: O(\(n^2\))过不去。
用手思考:应该是先把一棵子树搜完,再回溯,否则答案肯定不优。
设状态
设 f[x][L][R] 表示将 \(x\) 的子树从数字 \(L\) 连续标号到 \(R\) 花费的最小值。
这必 TLE/MLE 啊,空间都撑不住了。
设 f[x] 表示将 \(x\) 的子树从 \(1\) 开始标号花费的最小值,即 \(\sum\limits_{y \in x的子树} a[y]*b[y]\) , \(b\) 是一个 \(1\) 开头的排列
转移
状态的定义使得咱们在转移时要将 \(f[x]\) 加一个偏移量(说白了就是 \(b\) 整体加一个值)。
加入 \(f[y_1]\),\(f[y_2]\) 要合并到 \(f[x]\) 上面。
设 \(sum[x]=\sum\limits_{y \in x的子树}a[y]\)
那么有 \(f[x]=min(f[y_1]+f[y_2]+sum[y_2]*size[x_1],f[y_1]+f[y_2]+sum[y_1]*size[x_2])\)。
这比的就是先遍历 \(y_1\) ,还是 \(y_2\) 更优秀。
那么问题来了?
子节点多的话 O(\(p!\)) 必 T 啊,所以我放弃了这道题。
用头思考:可以按照 \(\frac{sum}{size}\) 从大到小排序,为什么自己想。
欸嘿!
这样就能 O(\(n\)) 求出以 \(root\) 为根的答案了。
#include<bits/stdc++.h>
#define Graph(x)for(int i=last[x],y=edge[i].ver;i;i=edge[i].next,y=edge[i].ver)
#define LL long long
using namespace std;
const int mod=1000000007;
int n,m,k,last[200010],num=0,a[200010];
int siz_e[200010];
LL sum[200010],f[200010],ans=1e18,allsum=0;
struct EDGE
{int ver,next;}edge[400010];
struct G
{int ver,size;LL sum;};
vector<G>g[200010];
inline int read()
{
int x=0,w=0;char ch=0;
while(!isdigit(ch)){w|=ch=='-';ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return w?-x:x;
}
void add(int U,int V)
{edge[++num]=(EDGE){V,last[U]};last[U]=num;}
bool cmp(G n1,G n2)
{return n1.sum*n2.size>n2.sum*n1.size;}
void dfs(int x,int F)
{
g[x].clear();
siz_e[x]=1;
f[x]=sum[x]=a[x];
Graph(x){
if(y==F)continue;
dfs(y,x);
siz_e[x]+=siz_e[y];
sum[x]+=sum[y];
f[x]+=f[y];
}
siz_e[0]=1;
Graph(x){
if(y==F)continue;
g[x].push_back({y,siz_e[y],sum[y]});
}
sort(g[x].begin(),g[x].end(),cmp);
for(int i=0,End=g[x].size();i<End;i++){
f[x]+=g[x][i].sum*siz_e[0];
siz_e[0]+=g[x][i].size;
}
}
int main()
{
freopen("signin.in","r",stdin);
freopen("signin.out","w",stdout);
n=read();
for(int i=1;i<n;i++){
int x=read(),y=read();
add(x,y);add(y,x);
}
for(int i=1;i<=n;allsum+=(a[i++]=read()));
for(int i=1;i<=n;i++){
dfs(i,0);
ans=min(ans,f[i]);
}
cout<<ans<<'\n';
return 0;
}
强烈建议先写一下这份代码。
= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = 我是分割线 = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =
你刚刚是不是说了以 root 为根?
是的,所以那份代码还是会 TLE。
啊这,我又放弃了这道题。
欸,等等好像有一个叫做 \({\color{Violet}换根DP}\) 的圣物。
用脑思考:这个换根好像很难。 \({\color{White}cjz:不,你就没脑子}\)
假设我们有了 \(f[x]\) ,思考怎么向 \(f[y]\) 转移。\({\color{White}cjz:像癌症一样转移}\)
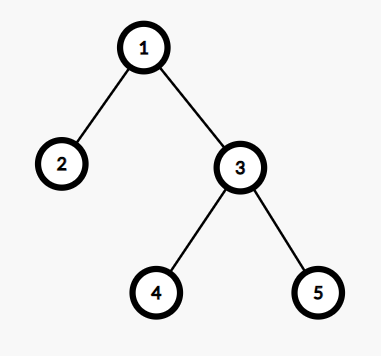
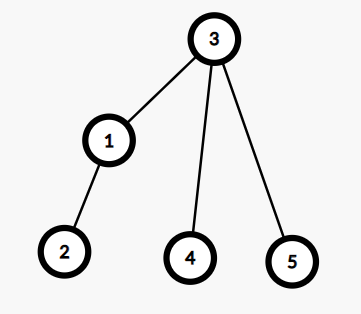
原先求 \(f[3]\) 时我们用的是 \(f[4]\),\(f[5]\),当我们从 1 转移到 3 是只不过是多了一个 \(f[1]\) 。
那着就好办了,转移时我们设父亲这一坨 \(f[fa]\) 是 \(ff\) ,他的子树大小是 _\(size\) ,他子树的权值和是 \(Sum\) 。
有:
LL sUm=a[x];//前面的权值和
_sIze=1;//前面的子树大小
for(int i=0,End=g[x].size();i<End;i++){//g[x] 是按照 sum/size 降序的。
if(g[x][i].ver!=F)//不能像 1 -> 2 ->1 ->2 ->1 这样打太极拳(云手这一式)
dp(g[x][i].ver,
x,
n-siz_e[g[x][i].ver],//父亲的大小很显然,n-儿子的大小
allsum-sum[g[x][i].ver],//父亲的权值和很显然,权值总和-儿子的权值和
f[x]-f[g[x][i].ver]-g[x][i].sum*_sIze-g[x][i].size*(allsum-sUm-g[x][i].sum)
//这个 ff 有点恶心,大体就是f[x]减去f[y]的贡献,但这造成了原来排在y后面的y2的标号变化
//需要抵消这个变化,后面所有点权和=点权总和-排在y前面的点权和(包括y)
);
sUm+=g[x][i].sum;
_sIze+=g[x][i].size;
}
#include<bits/stdc++.size>
#define Graph(x)for(int i=last[x],y=edge[i].ver;i;i=edge[i].next,y=edge[i].ver)
#define LL long long
using namespace std;
const int mod=1000000007;
int n,m,k,last[200010],num=0,a[200010];
int siz_e[200010];
LL sum[200010],f[200010],ans=1e18,allsum=0;
struct EDGE
{int ver,next;}edge[400010];
struct G
{int ver,size;LL sum;};
vector<G>g[200010];
inline int read()
{
int x=0,w=0;char ch=0;
while(!isdigit(ch)){w|=ch=='-';ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return w?-x:x;
}
void add(int U,int V)
{edge[++num]=(EDGE){V,last[U]};last[U]=num;}
bool cmp(G n1,G n2)
{return n1.sum*n2.size>n2.sum*n1.size;}
void dfs(int x,int F)
{
siz_e[x]=1;
f[x]=sum[x]=a[x];
Graph(x){
if(y==F)continue;
dfs(y,x);
siz_e[x]+=siz_e[y];
sum[x]+=sum[y];
f[x]+=f[y];
}
siz_e[0]=1;
Graph(x){
if(y==F)continue;
g[x].push_back({y,siz_e[y],sum[y]});
}
sort(g[x].begin(),g[x].end(),cmp);
for(int i=0,End=g[x].size();i<End;i++){
f[x]+=g[x][i].sum*siz_e[0];
siz_e[0]+=g[x][i].size;
}
}
void dp(int x,int F,int _size,LL Sum,LL ff)
{
f[x]=a[x]+ff;
int _sIze=1;
Graph(x){
if(y==F)continue;
f[x]+=f[y];
}
g[x].push_back({F,_size,Sum});
sort(g[x].begin(),g[x].end(),cmp);
for(int i=0,End=g[x].size();i<End;i++){
f[x]+=g[x][i].sum*_sIze;
_sIze+=g[x][i].size;
}
ans=min(ans,f[x]);
LL sUm=a[x];
_sIze=1;
for(int i=0,End=g[x].size();i<End;i++){
if(g[x][i].ver!=F)
dp(g[x][i].ver,
x,
n-siz_e[g[x][i].ver],
allsum-sum[g[x][i].ver],
f[x]-f[g[x][i].ver]-g[x][i].sum*_sIze-g[x][i].size*(allsum-sUm-g[x][i].sum)
);
sUm+=g[x][i].sum;
_sIze+=g[x][i].size;
}
}
int main()
{
freopen("signin.in","r",stdin);
freopen("signin.out","w",stdout);
n=read();
for(int i=1;i<n;i++){
int x=read(),y=read();
add(x,y);add(y,x);
}
for(int i=1;i<=n;i++){
a[i]=read();
allsum+=a[i];
}
dfs(1,0);
ans=f[1];
dp(1,0,0,0,0);
cout<<ans<<'\n';
return 0;
}


