递归与分治之棋盘覆盖问题
在一个2^k * 2^k个方格组成的棋盘中,若有一个方格与其他方格不同,则称该方格为一特殊方格,且称该棋盘为一个特殊棋盘。
显然特殊方格在棋盘上出现的位置有4^k种情形.因而对任何k≥0,有4^k种不同的特殊棋盘。
下图所示的特殊棋盘为 k=2 时 16 个特殊棋盘中的一个。
在棋盘覆盖问题中，要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格，且任何 2 个 L 型骨牌不得重叠覆盖。
易知，在任何一个 2^k * 2^k 的棋盘中，用到的 L 型骨牌个数恰为 (4^k-1)/3 。
求解棋盘问题，可利用分治的策略。当 k>0 时，将 2^k * 2^k 棋盘分割为 4 个 2^(k-1) * 2^(k-1) 子棋盘，如下图所示。
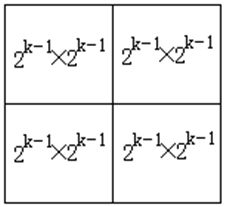
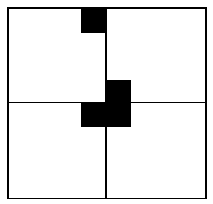
特殊方格必位于 4 个子棋盘之一，其余 3 个子棋盘中无特殊方格。用一个 L 型骨牌覆盖这 3 个较小的棋盘的汇合处，如图所示，将这 3 个无特殊方格的子棋盘转化为特殊棋盘，从而将原问题化为 4 个较小规模的棋盘覆盖问题。递归的使用 这种分割，直至棋盘简化为 1x1 棋盘。
python实现代码如下：
1 # coding =gbk 2 3 4 # tr左上角行号，tc左上角列号。dr特殊方格行号，dc特殊方格列号 5 def chessboard(board, size, tr, tc, dr, dc): 6 if size <= 1: 7 return 8 global tile 9 tile += 1 10 current_tile = tile 11 size //= 2 12 if dr < tr + size and dc < tc + size: 13 chessboard(board, size, tr, tc, dr, dc) 14 else: 15 board[tr + size - 1][tc + size - 1] = current_tile 16 chessboard(board, size, tr, tc, tr + size - 1, tc + size - 1) 17 if dr >= tr + size and dc < tc + size: 18 chessboard(board, size, tr + size, tc, dr, dc) 19 else: 20 board[tr + size][tc + size - 1] = current_tile 21 chessboard(board, size, tr + size, tc, 22 tr + size, tc + size - 1) 23 if dr < tr + size and dc >= tc + size: 24 chessboard(board, size, tr, tc + size, dr, dc) 25 else: 26 board[tr + size - 1][tc + size] = current_tile 27 chessboard(board, size, tr, tc + size, 28 tr + size - 1, tc + size) 29 if dr >= tr + size and dc >= tc + size: 30 chessboard(board, size, tr + size, tc + size, dr, dc) 31 else: 32 board[tr + size][tc + size] = current_tile 33 chessboard(board, size, tr + size, tc + size, 34 tr + size, tc + size) 35 36 37 tile = 0 38 chessboard_size = 4 39 board = [[0 for x in range(chessboard_size)] for y in range(chessboard_size)] 40 chessboard(board, chessboard_size, 0, 0, 1, 0) 41 42 board = [[row[i] for row in board] for i in range(len(board[0]))] 43 for lst in board: 44 print(lst)
