二维前缀和

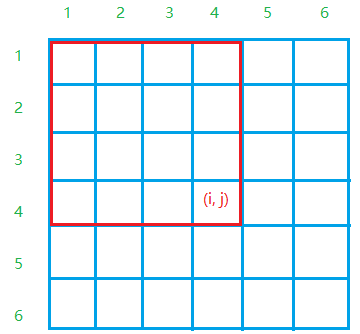
1. S[i,j]S[i,j]即为图1红框中所有数的的和为：

2. S[i,j]=S[i,j−1]+S[i−1,j]−S[i−1,j−1]+a[i,j]S[i,j]=S[i,j−1]+S[i−1,j]−S[i−1,j−1]+a[i,j]
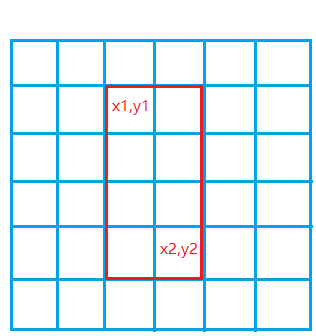
(x1,y1),(x2,y2)(x1,y1),(x2,y2)这一子矩阵中的所有数之和为：S[x2,y2]−S[x1−1,y2]−S[x2,y1−1]+S[x1−1,y1−1]

代码：

#include <iostream>

using namespace std;

const int N = 1010;

int a[N][N], s[N][N];

int main() {
    int n, m, q;
    cin >> n >> m >> q;

    for (int i = 1; i <= n; i++)//循环从1开始,a[0][0],s[0][0]都为0
        for (int j = 1; j <= m; j++) {
            scanf("%d", &a[i][j]);
            s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1] + a[i][j]; // 求前缀和
        }

    while (q--) {
        int x1,y1,x2,y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        // 算子矩阵的和
        printf("%d\n", s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]); 
    }

    return 0;
}