机器学习 降维算法: isomap & MDS
最近在看论文的时候看到论文中使用isomap算法把3D的人脸project到一个2D的image上。提到降维,我的第一反应就是PCA,然而PCA是典型的线性降维,无法较好的对非线性结构降维。ISOMAP是‘流形学习’中的一个经典算法,流形学习贡献了很多降维算法,其中一些与很多机器学习算法也有结合,先粗糙的介绍一下’流形学习‘。
流形学习
流形学习应该算是个大课题了,它的基本思想就是在高维空间中发现低维结构。比如这个图:
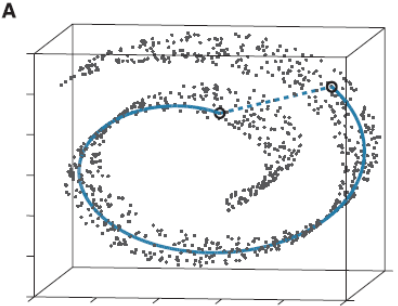
这些点都处于一个三维空间里,但我们人一看就知道它像一块卷起来的布,图中圈出来的两个点更合理的距离是A中蓝色实线标注的距离,而不是两个点之间的欧式距离(A中蓝色虚线)。
此时如果你要用PCA降维的话,它根本无法发现这样卷曲的结构(因为PCA是典型的线性降维,而图示的结构显然是非线性的),最后的降维结果就会一团乱麻,没法很好的反映点之间的关系。而流形学习在这样的场景就会有很好的效果。
经典MDS(Multidimensional Scaling)
如上文所述,MDS接收的输入是一个距离矩阵DD,我们把一些点画在坐标系里:

如果只告诉一个人这些点之间的距离(假设是欧氏距离),他会丢失那些信息呢?
a.我们对点做平移,点之间的距离是不变的。
b.我们对点做旋转、翻转,点之间的距离是不变的。
所以想要从D还原到原始数据X是不可能的,因为只给了距离信息之后本身就丢掉了很多东西,不过不必担心,即使这样我们也可以对数据进行降维(why?点这里)。
ISOMAP(等距特征映射)
其实线性流形方法无法在非线性流形上解决的问题,无非是需要解决两个问题:
1、如何测量流形上的几何距离?
2、如何将高维的2016维欧式空间映射到三维的低维空间?
首先,针对问题1,将MDS算法中的欧式距离换成“测地距离”,先抛一个“测地线的维基定义”。预热以后,我们来看经典的瑞士卷(图A),注意以下图A、B、C均来源于原文论文Fig3截图:
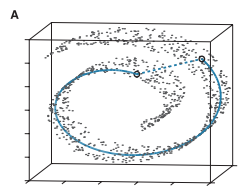
现在要我们把自己想象成是瑞士卷上的蚂蚁(对人类来说瑞士卷是三维的,对蚂蚁来说是二维的),上图A中的两个黑色圈圈为两只恩爱无比的蚂蚁,如何让这两只蚂蚁在最短的时间内见面呢?要走最短路径测地线蓝色线才是正道(直线最短?直接沿着虚线强行阔过去?你不想活了么?)因此,抛弃欧式距离,引来测地距离~
邻近点:直接计算邻近点之间的欧式空间距离
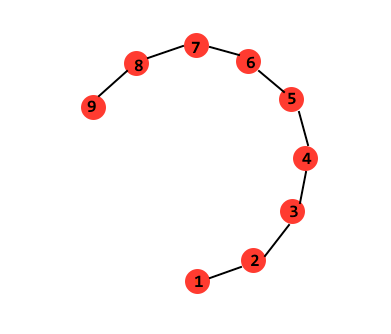
远距离的点:计算邻近点之间的最短距离连接成的序列,如下图所示(来源于博客),要计算空间中远距离的亮点1与9,计算1到9的最短路径1、2、3...9,沿着路径依次类推直到到达目的地9(根据流形中的全局非线性和局部线性属性):
最后形成如下图所示的瑞士卷上的逼近测地线,如下图B中的红色线条所示:
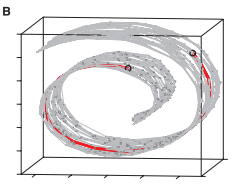
实现方法:引入图论框架,将数据作为图中的点,点与其邻近点之间使用边来连接,逼近的测地线使用最短路径代替。
Isomap算法流程如下:
步骤1:构建邻接图G(复杂度:O(DN2))
基于输入空间X中流形G上的的邻近点对i,j之间的欧式距离dx (i,j),选取每个样本点距离最近的K个点(K-Isomap)或在样本点选定半径为常数ε的圆内所有点为该样本点的近邻点,将这些邻近点用边连接,将流形G构建为一个反映邻近关系的带权流通图G;
步骤2:计算所有点对之间的最短路径(复杂度:O(DN2))
通过计算邻接图G上任意两点之间的最短路径逼近流形上的测地距离矩阵DG={dG(i,j)},最短路径的实现以Floyd或者Dijkstra算法为主。
步骤3:构建k维坐标向量(复杂度:O(dN2))
根据图距离矩阵DG={dG(i,j)}使用经典Mds算法在d维空间Y中构造数据的嵌入坐标表示(如下图C所示),选择低维空间Y的任意两个嵌入坐标向量yi与yj使得代价函数最小:
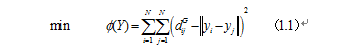
其中等式1.1的全局最优解可以通过将坐标向量yi设置为距离矩阵DG前d个特征值对应的特征向量来得到。
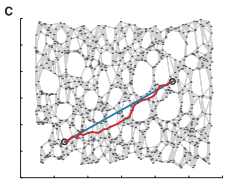
(还是偷懒了,没有去看看具体的例子,要用的时候再说把23333)
Reference:
[1] https://blog.csdn.net/dark_scope/article/details/53229427
[2] https://www.cnblogs.com/wing1995/p/5479036.html





