机器学习--激活函数篇
前言
在机器学习应用中,经常会使用一些激活函数,例如:sigmoid、ReLU等。这里简单记录总结一下为什么要用激活函数、怎么去选择激活函数
为什么要用激活函数
以下是激活函数具备的一些性质,也就是我们为什么要使用激活函数的原因:
- 非线性:当激活函数是非线性的时候,多次网络才能够去逼近任意的函数。
- 可微性:当优化的方法是基于梯度的方法的时候,这个性质是必须的。
- 单调性:当激活函数是单调函数的时候,单层的网络能够保证是凸函数。
- $f(x) \approx x$: 当激活函数满住这个性质的时候,如果参数的初始化是随机选取的一些较小的值,那么神经网络的训练一般会比较高效;如果不满足这个性质,那么就需要很用心的去设置初始值。
- 输出值的范围:当激活函数输出值是有限的时候,基于梯度的优化方法会更加稳定,因为特征的表示受有限权值的影响更显著;当激活函数的输出事无限的时候,模型的训练会更加高效,不过在这种情况下,一般需要较小的学习率(这段不是特别理解,实验做少了)
常见激活函数简介
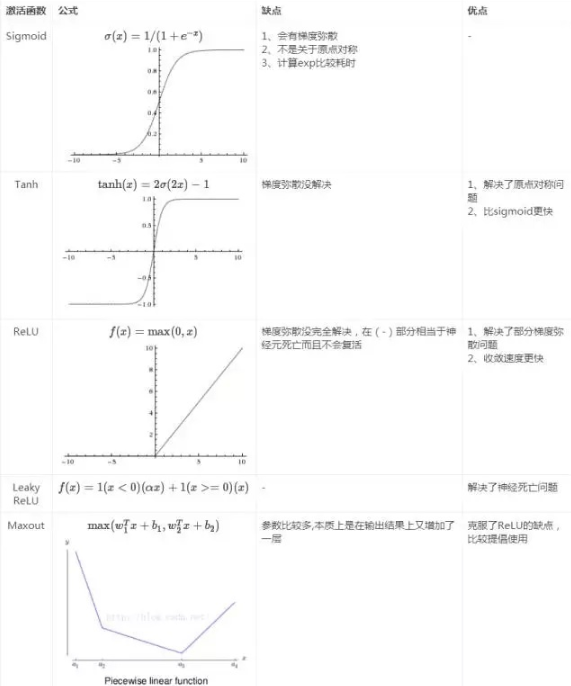
激活函数的发展经历了Sigmoid -> Tanh -> ReLU -> Leaky ReLU -> Maxout这样的过程,还有一个特殊的激活函数Softmax,因为它只会被用在网络中的最后一层,用来进行最后的分类和归一化。先贴一个总结的图:
Sigmoid
数学公式:
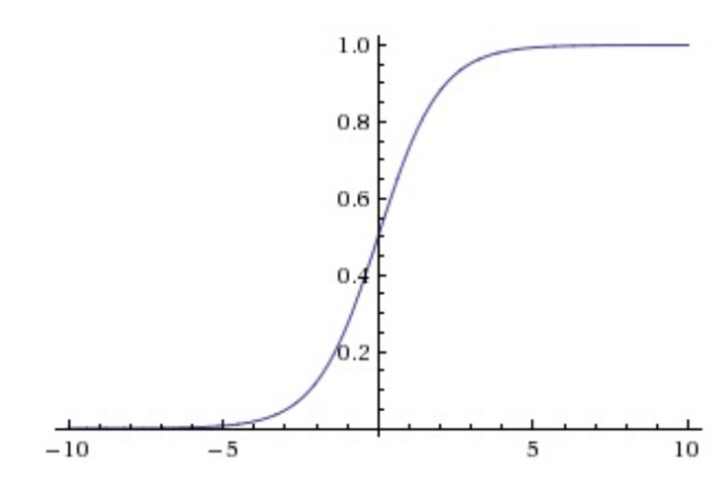
sigmoid非线性函数的数学公式是
函数图像如下图所示。它输入实数值并将其“挤压”到0到1范围内,适合输出为概率的情况,但是现在已经很少有人在构建神经网络的过程中使用sigmoid。
存在问题:
- Sigmoid函数饱和使梯度消失。当神经元的激活在接近0或1处时会饱和,在这些区域梯度几乎为0,这就会导致梯度消失,几乎就有没有信号通过神经传回上一层。
- Sigmoid函数的输出不是零中心的。因为如果输入神经元的数据总是正数,那么关于
的梯度在反向传播的过程中,将会要么全部是正数,要么全部是负数,这将会导致梯度下降权重更新时出现z字型的下降。
Tanh
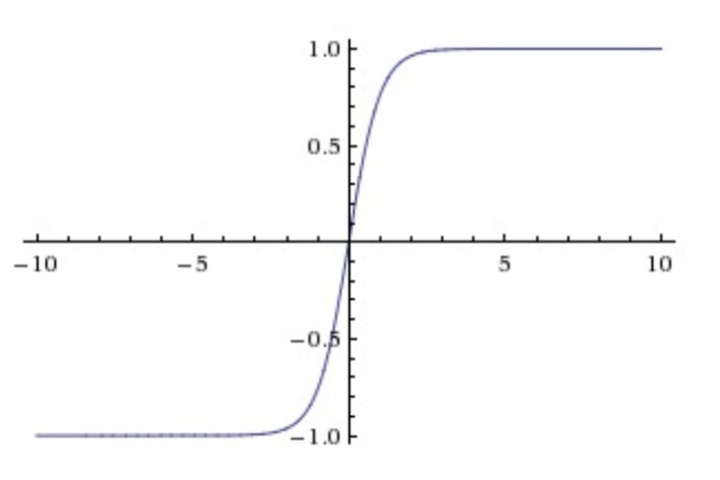
Tanh非线性函数的数学公式是
Tanh非线性函数图像如下图所示,它将实数值压缩到[-1,1]之间。
存在问题:
Tanh解决了Sigmoid的输出是不是零中心的问题,但仍然存在饱和问题。为了防止饱和,现在主流的做法会在激活函数前多做一步batch normalization,尽可能保证每一层网络的输入具有均值较小的、零中心的分布。
ReLU
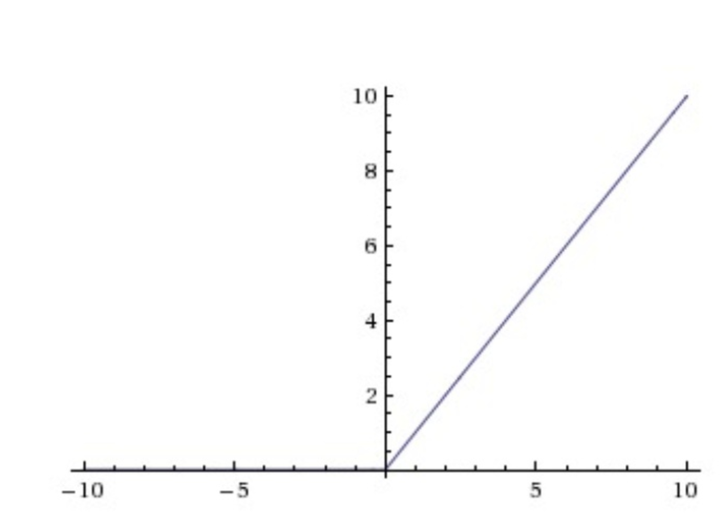
激活函数公式是
ReLU非线性函数图像如下图所示。相较于sigmoid和tanh函数,ReLU对于随机梯度下降的收敛有巨大的加速作用;sigmoid和tanh在求导时含有指数运算,而ReLU求导几乎不存在任何计算量。
对比sigmoid类函数主要变化是:
1)单侧抑制;
2)相对宽阔的兴奋边界;
3)稀疏激活性。
存在问题:
ReLU单元比较脆弱并且可能“死掉”,而且是不可逆的,因此导致了数据多样化的丢失。通过合理设置学习率,会降低神经元“死掉”的概率。
Leaky ReLU
函数公式:
其中 是很小的负数梯度值,比如0.01,Leaky ReLU非线性函数图像如下图所示。这样做目的是使负轴信息不会全部丢失,解决了ReLU神经元“死掉”的问题。更进一步的方法是PReLU,即把
当做每个神经元中的一个参数,是可以通过梯度下降求解的。
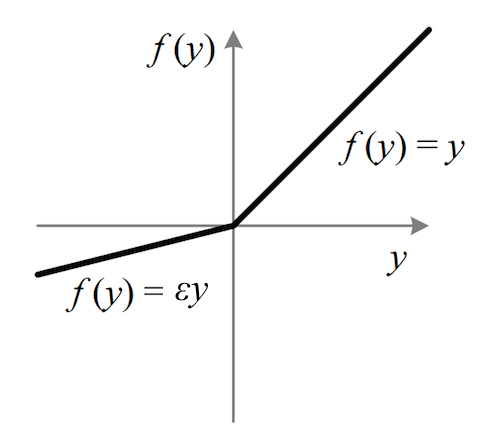
Maxout
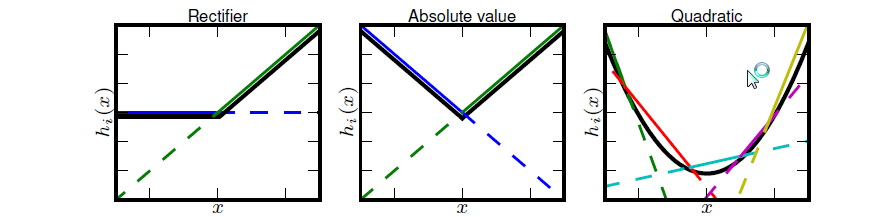
Maxout是对ReLU和leaky ReLU的一般化归纳,函数公式是
Maxout非线性函数图像如下图所示。Maxout具有ReLU的优点,如计算简单,不会 saturation,同时又没有ReLU的一些缺点,如容易go die。
存在问题:
每个神经元的参数double,这就导致整体参数的数量激增。
Softmax
Softmax用于多分类神经网络输出,目的是让大的更大。函数公式为:
示意图如下。
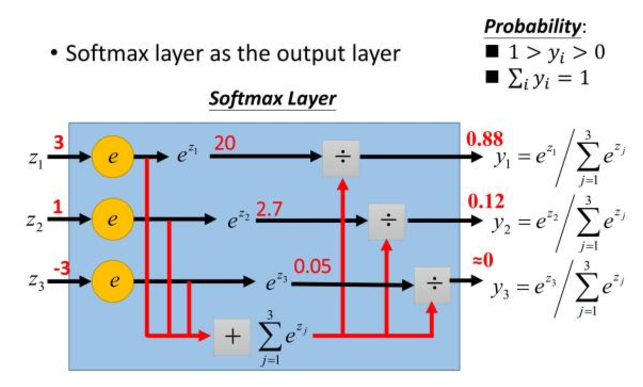
Softmax是Sigmoid的扩展,当类别数k=2时,Softmax回归退化为Logistic回归。




