面试排序算法总结

冒泡排序

　　冒泡排序是最基础的排序算法了，大体的思想是通过与相邻元素的比较和交换把小的数交换到最前面。不断的重复交换的过程，直到有一轮遍历没有发生交换。冒泡排序的时间复杂度为$O(n^{2})$。

　　代码如下：

class BubbleSort
{
public:
    void bubbleSort(vector<int>& arr)
    {
        if(arr == null || arr.length == 0)
            return ;
        for(int i=0; i<arr.size()-1; i++)
        {
            int flag = 0;　　　　　　　
            for(int j=arr.size()-1; j>i; j--)
            {
                if(arr[j] < arr[j-1])
                {
                    swap(arr, j-1, j);
                    flag = 1;
                }
            }
            if(flag == 0) break;
        }
    }

    void swap(vector<int>& arr, int i, int j)
    {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

选择排序

　　大致思想和冒泡一致，一次排序之后把最小的值放在最前面，但是过程不同。选择排序一次遍历的时候找到除了起始位置之外最小的值，然后考虑是否与其实位置的值交换。时间复杂度为$O(n^{2})$。代码如下：

　　

class SelectSort
{

public:
    void selectSort(vector<int>& arr)
    {
        if(arr == null || arr.size() == 0)
            return ;
        int minIndex = 0;
        for(int i=0; i<arr.size()-1; i++)   //只需要比较n-1次
        {
            minIndex = i;
            for(int j=i+1; j<arr.size(); j++)   //从i+1开始比较，因为minIndex默认为i了，i就没必要比了。
            {
                if(arr[j] < arr[minIndex])
                {
                    minIndex = j;
                }
            }
            if(minIndex != i)   //如果minIndex不为i，说明找到了更小的值，交换之。
            {
                swap(arr, i, minIndex);
            }
        }

    }
    void swap(vector<int>& arr, int i, int j)
    {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

}

插入排序：

　　依次枚举数组的每个index,在枚举的时候保证index之前的数是有序的。在枚举到i的时候，有序的插入到[0,i-1]子数组中，重复上述步骤即可。代码如下：

　　

void insertSort(vector<int>& arr)
    {
        if(arr == null || arr.size() == 0)
            return ;

        for(int i=1; i<arr.size(); i++)   //假设第一个数位置时正确的；要往后移，必须要假设第一个。
        {

            int j = i;
            int target = arr[i]; //待插入的

            //后移
            while(j > 0 && target < arr[j-1])
            {
                arr[j] = arr[j-1];
                j --;
            }

            //插入
            arr[j] = target;
        }

    }

快速排序：

　　快速排序可以理解为冒泡排序的一个改进，冒泡排序是通过相邻元素的比较和交换把最小的冒泡到最顶端，而快速排序是比较和交换小数和大数，这样一来不仅把小数冒泡到上面同时也把大数沉到下面。

　　举个栗子：对$5,3,8,6,4$这个无序序列进行快速排序，思路是右指针找比基准数小的，左指针找比基准数大的，交换之。

　　$5,3,8,6,4$ 用5作为比较的基准，最终会把5小的移动到5的左边，比5大的移动到5的右边。

　　$5,3,8,6,4$首先设置$i,j$两个指针分别指向两端，$j$指针先扫描4比5小停止。然后$i$扫描，8比5大停止。交换$i,j$位置。

　　$5,3,4,6,8$然后$i$指针再扫描，这时j扫描4时两指针相遇。停止。然后交换4和基准数。

　　$4,3,5,6,8$ 一次划分后达到了左边比5小，右边比5大的目的。之后对左右子序列递归排序，最终得到有序序列。

　　

int Partition(vector<int>& arr,int left,int right)
{
   int tmp = arr[left];
   while(left < right)
   {
       while(left < right && arr[right] >= tmp) right--;
       arr[left] = arr[right];
       while(left < right && arr[left] <= tmp) left++;
       arr[right] = arr[left];
   }
   arr[left] = tmp;
   return left;
}

void quickSort(vector<int>& arr, int left, int right)
{
    if(left >= right)
        return ;
    int pivotPos = Partition(arr, left, right);
    quickSort(arr, left, pivotPos-1);
    quickSort(arr, pivotPos+1, right);
}

堆排序：

　　简单说一下堆排序的基本思路:

　　a.将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

　　b.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

　　c.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

　　简单说明一下如何条件结构，首先找到最后一个非叶子节点（这里用数组模拟树的化，第一个非叶子节点为arr.size()-1），从左至右，从上到下调整。例如对于初始的状态：

　　

 

 　　我们从index = 1的节点开始调整：

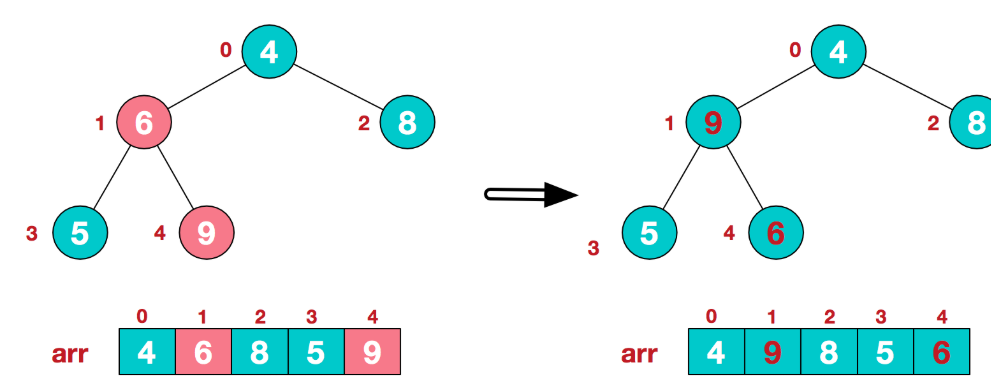　　这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

 

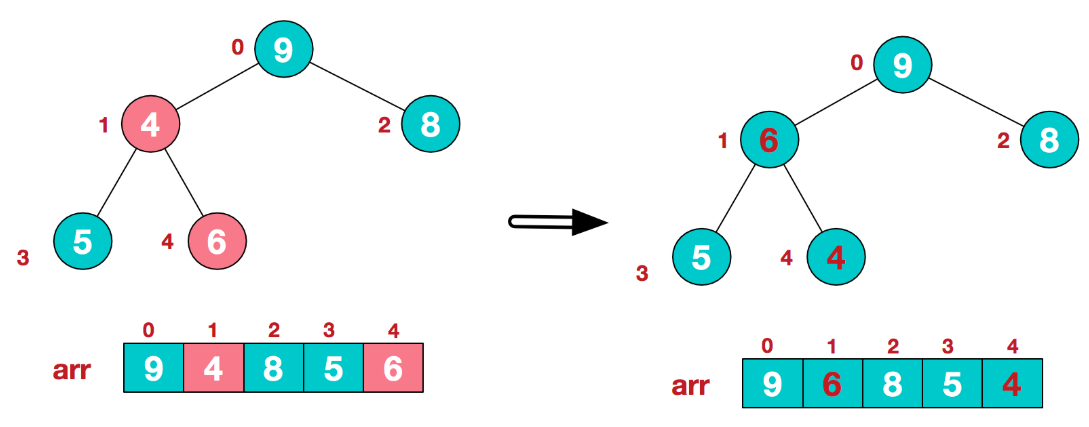
 　　这样一个大根堆就调整好了。之后不断的将末尾的数换至数组起始位置进行调整就好了，代码如下:

class HeapSort
{

    public：
    void Sort(vector<int>& arr)
    {
        //1.构建大顶堆
        for(int i=arr.size()/2-1; i>=0; i--)
        {
            //从第一个非叶子结点从下至上，从右至左调整结构
            adjustHeap(arr,i,arr.size());
        }
        //2.调整堆结构+交换堆顶元素与末尾元素
        for(int j=arr.size()-1; j>0; j--)
        {
            swap(arr,0,j);//将堆顶元素与末尾元素进行交换
            adjustHeap(arr,0,j);//重新对堆进行调整
        }

    }

    /**
     * 调整大顶堆（仅是调整过程，建立在大顶堆已构建的基础上）
     * @param arr
     * @param i
     * @param length
     */
    void adjustHeap(vector<int>& arr,int i,int length)
    {
        int temp = arr[i];//先取出当前元素i
        for(int k=i*2+1; k<length; k=k*2+1) //从i结点的左子结点开始，也就是2i+1处开始 不断的向下调整
        {
            if(k+1<length && arr[k]<arr[k+1]) //如果左子结点小于右子结点，k指向右子结点
            {
                k++;
            }
            if(arr[k] >temp) //如果子节点大于父节点，将子节点值赋给父节点（不用进行交换）
            {
                arr[i] = arr[k];
                i = k;
            }
            else
            {
                break;
            }
        }
        arr[i] = temp;//将temp值放到最终的位置
    }

    /**
     * 交换元素
     * @param arr
     * @param a
     * @param b
     */
    void swap(int []arr,int a,int b)
    {
        int temp=arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }
}

希尔排序：

（待整理）　　

归并排序：

　　

https://www.cnblogs.com/wxisme/p/5243631.html