机器学习--逻辑回归(LR)
1. 模型介绍
Logistic Regression 虽然被称为回归,但其实际上是分类模型,并常用于二分类。Logistic Regression 因其简单、可并行化、可解释强深受工业界喜爱。在正式介绍模型之前,先聊一聊Logitstic分布。
1.1 逻辑斯谛分布(logistic distribution)
Logistic分布是一种连续型的概率分布,其分布函数和密度函数分别为:
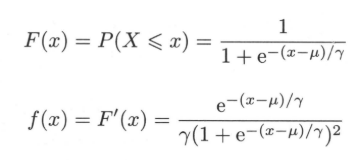
其中,$\mu$表示位置参数,$\gamma > 0$为形状参数。logistic分布函数的图形是一条S形曲线。该曲线以点$(\mu,\frac{1}{2})$为中心对称,既满足$F(-x+\mu) - \frac{1}{2} = -F(x+\mu) + \frac{1}{2}$。曲线在中心附近增长速度较快,在两端速度较慢。形状参数$\gamma$的值越小,曲线在中心附近增长越快。$f(x)$、$F(x)$曲线如下所示:
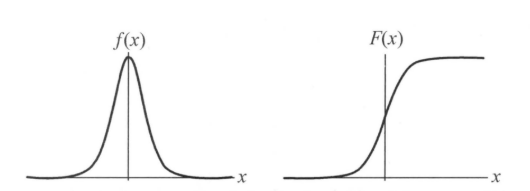
1.2 逻辑斯蒂回归模型
先给出二项逻辑斯谛回归模型的条件概率分布:
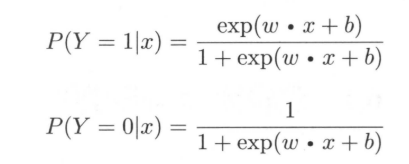
这里,$X \in R^{n}$是输入,$Y \in {0,1}$是输出,$w \in R^{n}$和$b \in R$是参数,$w$为权值向量,$b$为偏置,$w \cdot x$为$w$和$b$的内积。对于给定的输入实例x,按照上述公式计算出$P(Y = 1|X)$以及$P(Y = 0|x)$。逻辑斯蒂回归比较两个条件概率值的大小,将实例$x$分到概率值较大的那一类。
接下来聊聊逻辑斯蒂回归模型的特点。先给出一个定义:一个事件的几率(odds)是指该事件发生的概率与该事件不发生的概率的比值。如果事件发生的概率是$p$,那么该事件的几率是$\frac{p}{1-p}$,该事件的对数几率(log odds)或者logit函数为:$logit(p) = log\frac{p}{1-p}$。对逻辑斯蒂而言,其logit函数为:
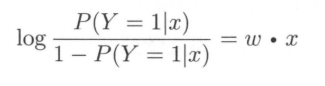
也就是说,在LR模型,输出$Y = 1$的对数几率为输入$X$的线性函数。换一个角度看,考虑对输入$X$进行分类的线性函数$w \cdot x$,其值域为实数域,LR(按照logistic分布)将其转换为概率:

这个时候,线性函数的值越接近正无穷,概率值就越接近1;线性函数的值越接近负无穷,概率值越接近0,这样的模型就是逻辑斯蒂回归模型。通过上述的一个推导,我们可以发现LR实际上是使用线性模型的预测值逼近分类任务真实标记的对数几率,有以下几个优点:
- 直接对分类概率建模,不需要假设数据分布,从而避免了假设分布不准确带来的问题;
- 不仅可以预测出类别,还可以得到该预测的概率,这对一些利用概率辅助决策的任务很有帮助;
- 对数几率是任意阶可导的凸函数,有许多数值优化的算法可以求出最优解。
1.3 模型参数估计
LR在学习的时候,对于给定的训练数据集$T = {(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{N},y_{N})}$,其中,$x_{i} \in R^{n}$,$y_{i} \in {0,1}$,可以用极大似然估计估计模型参数。
假设:

似然函数为:
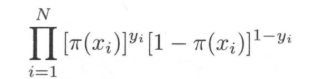
对数似然函数为:

对于$L(w)$求极大值,能够得到$w$的估计值。求解的方式一般采用的是梯度下降法,这里需要求出$L(w)$的一阶导,如下所示:
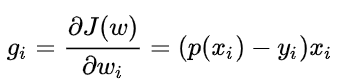
(后续要补一个手推的过程)





