Leetcode 184周赛题解

前一宿没睡好，困的不行，写的有点慢..

5380. 数组中的字符串匹配

题目描述：

　　给你一个字符串数组 words ，数组中的每个字符串都可以看作是一个单词。请你按 任意 顺序返回 words 中是其他单词的子字符串的所有单词。如果你可以删除 words[j] 最左侧和/或最右侧的若干字符得到 word[i] ，那么字符串 words[i] 就是 words[j] 的一个子字符串。

题解:

　　两次遍历，用kmp判断一下是否是字串。

AC代码：

class Solution {
public:
    int Next[100010];
void getNext(string s)
{
    int i,j;
    i=0;
    j=-1;
    int len=s.length();
    Next[0]=-1;
    while(i<len && j<len)
    {
        if(j==-1 || s[i]==s[j]) Next[++i]=++j;
        else j=Next[j];
    }
}
bool kmp(string m,string s) // s对应子串
{
    getNext(s);
    int i,j;
    i=j=0;
    int mlen=m.length();// i
    int slen=s.length();// j
    while(i<mlen && j<slen)
    {
        if(j==-1 || m[i]==s[j]) i++,j++;
        else j=Next[j];
    }
    if(j==slen) return true;
    return false;
}
    vector<string> stringMatching(vector<string>& words) {
        vector<string> ans;
        int Len = words.size();
        if(Len == 0) return {};
        for(int i=0;i<Len;i++)
        {
            for(int j=0;j<Len;j++)
            {
                if(i == j) continue;
                if(kmp(words[j],words[i])) 
                {
                    ans.push_back(words[i]);
                    break;
                }
            }
        }
        return ans; 
    }
};

5381. 查询带键的排列

题目描述：

　　给你一个待查数组 queries ，数组中的元素为 1 到 m 之间的正整数。 请你根据以下规则处理所有待查项 queries[i]（从 i=0 到 i=queries.length-1）：

• 一开始，排列 P=[1,2,3,...,m]。
• 对于当前的 i ，请你找出待查项 queries[i] 在排列 P 中的位置（下标从 0 开始），然后将其从原位置移动到排列 P 的起始位置（即下标为 0 处）。注意， queries[i] 在 P 中的位置就是 queries[i] 的查询结果。

　　请你以数组形式返回待查数组  queries 的查询结果。

题解：暴力模拟

class Solution {
public:
    vector<int> processQueries(vector<int>& queries, int m) {
        vector<int> p;
        for(int i=1;i<=m;i++) p.push_back(i);
        vector<int> ans;
        for(auto & que:queries)
        {
            auto pos = p.begin();
            int cnt = 0;
            while(pos != p.end()) 
            {
                if(*pos == que) break;
                pos++;
                cnt++;
            }
            ans.push_back(cnt);
            
            p.erase(pos);
            p.insert(p.begin(),que);
            
        }
        return ans;
    }
};

 

5382. HTML 实体解析器

题目描述：

「HTML 实体解析器」 是一种特殊的解析器，它将 HTML 代码作为输入，并用字符本身替换掉所有这些特殊的字符实体。HTML 里这些特殊字符和它们对应的字符实体包括：

• 双引号：字符实体为 " ，对应的字符是 " 。
• 单引号：字符实体为 ' ，对应的字符是 ' 。
• 与符号：字符实体为 & ，对应对的字符是 & 。
• 大于号：字符实体为 > ，对应的字符是 > 。
• 小于号：字符实体为 < ，对应的字符是 < 。
• 斜线号：字符实体为 ⁄ ，对应的字符是 / 。

给你输入字符串 text ，请你实现一个 HTML 实体解析器，返回解析器解析后的结果。

题解:

　　根据&判断是否开始替换，用map存一下映射关系就好了。

AC代码:

class Solution {
public:
    string entityParser(string text) {
        map<string,string> mp;
        mp["&quot;"] = "\"";
        mp["&apos;"] = "'";
        mp["&amp;"] = "&";
        mp["&gt;"] = ">";
        mp["&lt;"] = "<";
        mp["&frasl;"] = "/";
        int Len = text.length();
        string ans;
        for(int i=0;i<Len;)
        {
            if(text[i] == '&')
            {
                string tmp = "&";
                i++;
                while(i<Len && mp.find(tmp) == mp.end()) 
                {
                    if(text[i] == '&') break;
                    tmp += text[i];
                    
                    i++;
                }
                // if(i<Len && text[i] != '&') i++; 
                if(mp.find(tmp) != mp.end()) ans+=mp[tmp];
                else ans += tmp;
                // cout << tmp << endl;
            }
            else 
            {
                ans += text[i];
                i++;
            }
            
        }
        return ans;
    }
};

5383. 给 N x 3 网格图涂色的方案数

题目描述：

　　你有一个 n x 3 的网格图 grid ，你需要用 红，黄，绿 三种颜色之一给每一个格子上色，且确保相邻格子颜色不同（也就是有相同水平边或者垂直边的格子颜色不同）。给你网格图的行数 n 。请你返回给 grid 涂色的方案数。由于答案可能会非常大，请你返回答案对 10^9 + 7 取余的结果。

题解:

　　这个就比较烦了，我用的是dp。先看下图（当n=1的时候）：

 

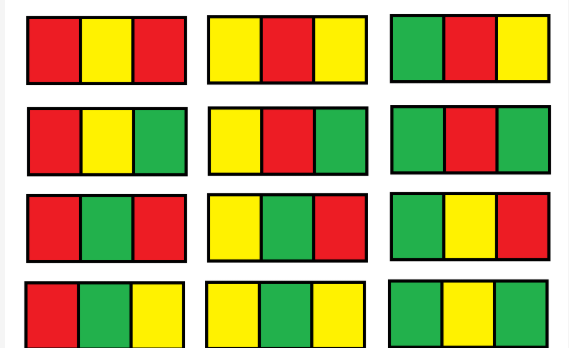
 　 从左到右，从上到下依次编号，那么一共有12个状态。定义一个二维$dp[i][j]$，表示第$i$个$grid$为状态$j$的时候有多少种涂色方法。状态转移比较麻烦，我举个例子

$dp[i][0] =  (dp[i-1][1]%mod + dp[i-1][2]%mod + dp[i-1][4]%mod + dp[i-1][5]%mod + dp[i-1][10]%mod)%mod; $当第$i$个$gird$状态为$0$的时候，第$i-1$个grid合法的状态为$1，2，4，5，10$(根据题目推一下就好了)

AC代码：

class Solution {
public:
    int numOfWays(int n) {
        long long  dp[n+1][12];
        memset(dp,0,sizeof(dp));
        long long mod = 1000000007;
        for(int i=0;i<12;i++) dp[1][i] = 1;
        for(int i=2;i<=n;i++)
        {
            dp[i][0] = (dp[i-1][1]%mod + dp[i-1][2]%mod + dp[i-1][4]%mod +  dp[i-1][5]%mod + dp[i-1][10]%mod)%mod;
            dp[i][3] = (dp[i-1][1]%mod + dp[i-1][2]%mod + dp[i-1][7]%mod + dp[i-1][10]%mod)%mod;
            dp[i][6] = (dp[i-1][1]%mod + dp[i-1][2]%mod + dp[i-1][4]%mod +  dp[i-1][5]%mod + dp[i-1][11]%mod)%mod;
            dp[i][9] = (dp[i-1][4]%mod + dp[i-1][5]%mod + dp[i-1][8]%mod +  dp[i-1][11]%mod)%mod;
            
            dp[i][1] = (dp[i-1][0]%mod + dp[i-1][3]%mod + dp[i-1][6]%mod + dp[i-1][8]%mod +dp[i-1][11]%mod)%mod;
            dp[i][4] = (dp[i-1][0]%mod + dp[i-1][6]%mod + dp[i-1][9]%mod +dp[i-1][8]%mod)%mod;
            dp[i][7] = (dp[i-1][3]%mod + dp[i-1][2]%mod + dp[i-1][5]%mod +dp[i-1][11]%mod)%mod;
            dp[i][10] = (dp[i-1][0]%mod +dp[i-1][3]%mod + dp[i-1][5]%mod + dp[i-1][8]%mod +dp[i-1][11]%mod)%mod;
            
            dp[i][2] = (dp[i-1][0]%mod +dp[i-1][3]%mod + dp[i-1][6]%mod + dp[i-1][7]%mod)%mod;
            dp[i][5] = (dp[i-1][0]%mod +dp[i-1][6]%mod + dp[i-1][7]%mod + dp[i-1][9]%mod +dp[i-1][10]%mod)%mod;
            dp[i][8] = (dp[i-1][1]%mod +dp[i-1][4]%mod + dp[i-1][9]%mod + dp[i-1][10]%mod)%mod;
            dp[i][11] = (dp[i-1][1]%mod +dp[i-1][6]%mod + dp[i-1][7]%mod + dp[i-1][9]%mod +dp[i-1][10]%mod)%mod;   
        }
        long long ans = 0;
        for(int i=0;i<12;i++)
        {
            ans = (ans + dp[n][i])%mod;
        }
        return ans;
    }
};

 

困的一批..下午出去休息一下 这破状态