Leetcode 1349 参加考试的最大学生数

题目描述：

 

 

 

 

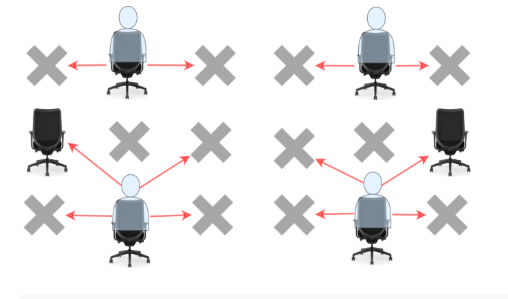
 题解：

考虑到一个学术只能看到同一行或者前一行同学的试卷，具有一定的顺序，考虑动态规划。考虑状压dp，定义dp[i][j]表示到i行为止，第i行状态为j时的

最大可坐学生个数，其中j用二进制展开，为1的位置表示坐了学生。状态转移方程为dp[i][j] = max(dp[i-1][k]+k.count,dp[i][j])

AC代码：

class Solution {
public:
    // 状态压缩
    int count(int j)
    {
        int ans = 0;
        while(j)
        {
            if(j%2 == 1) ans++;
            j = j/2;
        }
        return ans;
    }

    // 判断这个位置是否合法
    int judge(int i,int j,vector<vector<char> > seats)
    {
        int col = i;
        int row = 0;
        while(j)
        {
            if(j%2 == 1 && seats[col][row] == '#') return -1;
            j/=2;
            row++;
        }
        return 1;
    }
    
    // k,j是否有影响
    int judge2(int k, int j)
    {
        int tmp = k | j;
        int pre = 0;
        while(tmp)
        {
            if(tmp%2 == 1 && pre == 1) return -1;
            pre = tmp%2;
            tmp = tmp/2;
        }
        return 1;
    }

    int maxStudents(vector<vector<char>>& seats) {
         int dp[9][1<<8];
         int n = seats.size();
         int m = seats[0].size();
         // cout << (1<<8) <<endl;
         for(int i=0;i<n;i++)
         {
             for(int j=0;j<(1<<m);j++) dp[i][j] = 0;
         }
         for(int i=0;i<n;i++)
         {
             for(int j=0;j<(1<<m);j++)
             {
                 int tmp = count(j);   
                 if(i == 0)
                 {
                     if(judge(i,j,seats) == 1) dp[i][j] = tmp; 
                 }
                 else
                 {
                     if(judge(i,j,seats) == 1)
                     {
                         for(int k=0;k<(1<<m);k++) 
                            if(judge2(k,j) == 1 && judge(i-1,k,seats) == 1) dp[i][j] = max(dp[i][j],dp[i-1][k]+tmp);
                     }
                 }
             }
         }
         int mx = INT_MIN;
         return mx;
    }
};