机器学习--随机森林

　　在集成学习方法的两个流派中，boosting流派特点是各个弱学习器之间有依赖关系；bagging流派的特点是各个弱学习器之间没有依赖关系，可以并行拟合。本文就对集成学习中Bagging与随机森林算法做一个总结。

一、Bagging介绍

　　先看一个Bagging的一个概念图(图来自https://www.cnblogs.com/nickchen121/p/11214797.html)

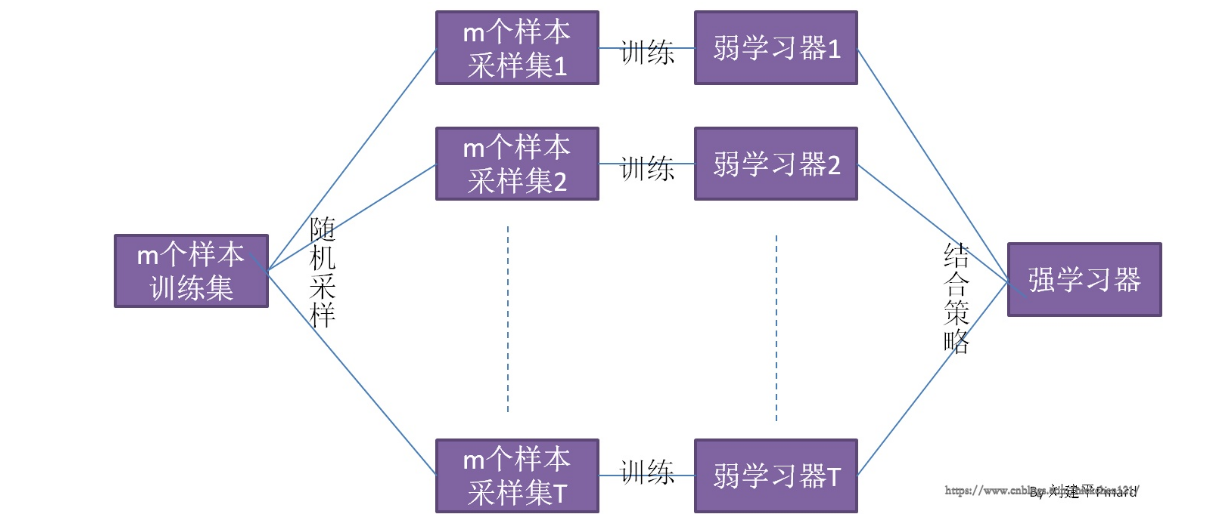
 　　从上图可以看出，Bagging的弱学习器之间的确没有boosting那样的联系。它的特点在“随机采样”。那么什么是随机采样？随机采样(bootsrap)就是从我们的训练集里面采集固定个数的样本，但是每采集一个样本后，都将样本放回。也就是说，之前采集到的样本在放回后有可能继续被采集到。　　对于我们的Bagging算法，一般会随机采集和训练集样本数m一样个数的样本。这样得到的采样集和训练集样本的个数相同，但是样本内容不同。如果我们对有m个样本训练集做T次的随机采样，则由于随机性，T个采样集各不相同。　　

　　注意到这和GBDT的子采样是不同的。GBDT的子采样是无放回采样，而Bagging的子采样是放回采样。对于一个样本，它在某一次含m个样本的训练集的随机采样中，每次被采集到的概率是$\frac{1}{m}$。不被采集到的概率为$1-(\frac{1}{m})$。如果m次采样都没有被采集中的概率是$(1-\frac{1}{m})^m$.当m趋近于无穷的时候,$(1-\frac{1}{m})^m$趋近于$\frac{1}{e}$。也就是说，在bagging的每轮随机采样中，训练集中大约有36.8%的数据没有被采样集采集中。对于这部分大约36.8%的没有被采样到的数据，我们常常称之为袋外数据(Out Of Bag, 简称OOB)。这些数据没有参与训练集模型的拟合因此可以用来检测模型的泛化能力。

　　bagging对于弱学习器没有限制，这和Adaboost一样。但是最常用的一般也是决策树和神经网络。bagging的集合策略也比较简单，对于分类问题，通常使用简单投票法，得到最多票数的类别或者类别之一为最终的模型输出。对于回归问题，通常使用简单平均法，对T个弱学习器得到的回归结果进行算术平均得到最终的模型输出。由于Bagging算法每次都进行采样来训练模型，因此泛化能力很强，对于降低模型的方差很有作用。当然对于训练集的拟合程度就会差一些，也就是模型的偏倚（bias）会大一些。Bagging算法流程如下所示：

　　

 

 

 

 

 

 

 

 

二、 Random Forest介绍

2.1　Random Forest理论基础　

　　理解了Bagging算法自然就好理解RF了。 RF是Bagging的一个改进，它的思想仍然是bagging,但是进行了独有的改进。

　　首先，RF选择CART作为弱学习器（这点和GBRT类似），这点类似于GBDT。其次RF对决策树做了改进，对于普通的决策树，我们会在节点上所有的n个样本特征中选择一个最优的特征来做决策树的左右子树划分，但是RF通过随机选择节点上的一部分样本特征，这个数字小于n，记作$n_{sub}$。然后在这些随机选择的$n_{sub}$中选择一个最优的特征来做决策树的左右子树叶划分。这样进一步增强了模型的泛化能力。

　　如果$n_{sub}$越小，则此时的RF的CART决策树和普通的CART决策树没有什么区别。$n_{sub}$越小，RF越鲁棒，对应的其拟合的程度会变差，对应的方差小，bias偏大。实际的使用过程中就需要用CV来选择一个合适的值。(Bagging和RF主要的区别应该是RF使用的是CART，且RF对CART划分的规则上做了一些修改，不是对所有属性选择最优，而是随机选取一部分属性，然后从这部分属性中选最优）

　　除了上面两点，RF和普通的bagging算法没有什么不同， 下面简单总结下RF的算法。

　　　　输入为样本集$D = {(x,y1),(x2,y2),...{xm,ym}}$，弱分类器迭代次数T。

　　　　输出为最终的强分类器$f(x)$

　　　　1）对于$t=1,2...,T$:

　　　　　　a)  对训练集进行第t次随机采样，共采集m次，得到包含m个样本的采样集$D_{t}$

　　　　　　b）用采样集合训练$D_{t}$对应的第$t$个决策树模型$G_{t}(x)$，在训练决策树模型的节点的时候，在节点上所有的样本特征中选择一部分特征，在这些随机选择的样本特征中选择一个最优特征来做决策树的分裂节点。

　　　　2) 如果是分类算法预测，则T个弱学习器投出最多票数的类别或者类别之一为最终类别。如果是回归算法，T个弱学习器得到的回归结果进行算术平均得到的值为最终的模型输出。

　　【随机特征】和【随机数据】这两个随机性的引入对随机森林的分类性能至关重要。由于它们的引入，使得随机森林不容易陷入过拟合，并且具有很好得抗噪能力（比如：对缺省值不敏感）。也正因为如此，随机森林相比CART决策树还有另外一个特点，那就是：通常情况下， 随机森林不需要剪枝。

 

2.2 特征重要性

　　基于树的集成算法还有一个很好的特性，就是模型训练结束后可以输出模型所使用的特征的相对重要度，便于我们选择特征，理解哪些因素是对预测有关键影响。在随机森林中，一般来说，某一特征在所有树中离树根的平均距离越近，这个特征在给定的任务中就越重要。常见有两种计算特征重要性的方法：基于基尼系数、基于oob 袋外数据。

• 基于基尼系数。随机森林中每棵树都是CART决策树，因此树在选择向下分裂的特征时，都是基于基尼系数。假设某特征的在某一棵树上的节点m向下分裂，分裂前的基尼系数为 $GI$ ，分裂后，左右分支的基尼系数分别为 $GIL$ 、$GIR$，则$VIm = GI - (GIL+GIR)$。假如在这颗树上，该特征分裂了k次，则在这棵树上的重要性为$\sum_{i = 1}^{k}{VIM}$。假设随机森林中，共有n棵树用到这个特征，则整个森林中整个特征的重要性为$\sum^{n}{\sum_{i = 1}^{k}{VIM}}$。最后把所有求得的M个特征重要性评分进行归一化处理就得到重要性的评分。
• 基于袋外数据。

　　　　1. 对于随机森林中的每一颗决策树,使用相应的OOB(袋外数据)数据来计算它的袋外数据误差,记为errOOB1。

　　　　2. 随机地对袋外数据OOB所有样本的特征X加入噪声干扰，再次计算它的袋外数据误差,记为errOOB2。

　　　　3. 假设随机森林中有N棵树,那么对于特征X的重要性 $\sum{(errOOB1-errOOB2)/N}$

　　之所以可以用这个表达式来作为相应特征的重要性的度量值是因为：若给某个特征随机加入噪声之后，袋外的准确率大幅度降低，则说明这个特征对于样本的分类结果影响很大，也就是说它的重要程度比较高。

　　而该方法中涉及到的对数据增加噪音或者进行打乱的方法通常有两种：

　　1. 是使用uniform或者gaussian抽取随机值替换原特征；

　　2. 是通过permutation的方式将原来的所有N个样本的第 i 个特征值重新打乱分布（相当于重新洗牌）

三、随机森林小结

　  RF作为一个可以高度并行优化的算法，在大数据集上大有可为。这里也对常规的随机森林算法的优缺点做一个小结。

　　RF的主要优点有：

　　　　1） 训练可以高度并行化，对于大数据时代的大样本训练速度有优势。个人觉得这是的最主要的优点。

　　　　2） 能处理高维度的数据，随机特征性也使其不用进行特征选择。

　　　　3） 在训练后，能够输出各特征的重要性。

　　　　4） 由于采用了随机采样，训练出的模型的方差小，泛化能力强。

　　　　5） 相对于Boosting系列的Adaboost和GBDT， RF实现比较简单。

　　　　6） 对部分特征缺失不敏感。

　　RF的主要缺点有：

　　　　1）在某些噪音比较大的样本集上，RF模型容易陷入过拟合。

　　　　2)  取值划分比较多的特征容易对RF的决策产生更大的影响，从而影响拟合的模型的效果。（这里也可以从基尼系数的角度去理解）

 　　（2020.4.21）对于RF的缺点这里做一些补充说明。首先是第一个缺点，对于噪声较多的数据，RF容易拟合到噪声上去，导致模型向噪音数据偏离，进而陷入过拟合。对于第二点，我们举例子来说，特征A有2个离散特征A1,A2， 特征B有三个离散特征B1,B2,B3. 如果你选择A来分裂，那么A1和A2已经在不同子树，每个子树里的特征A的取值已经一样。后续已经没有机会再做分裂标准了，如果选择的是B，假设分裂的二叉树是B1,B2左子树，B3右子树，那么左子树里B还有机会在下一次分裂的时候被选中，这样机会就多一次了。