精通特征工程笔记(一)

发数值部分

　　处理计数问题,对于大规模的数据,在实际处理的时候要考虑是保留原始的数值类型还是转成二值数,或者粗粒度的分箱操作.对于衡量可以二分类的数据,如果存在个别极端大的数值的数据会对带跑整体的预测,这个时候就需要设置一个threshold对数据二值化处理.下面主要记录一下分箱方法.

　　yelp数据是用户点评商家的数据集分布图如下所示:

　　

 

 

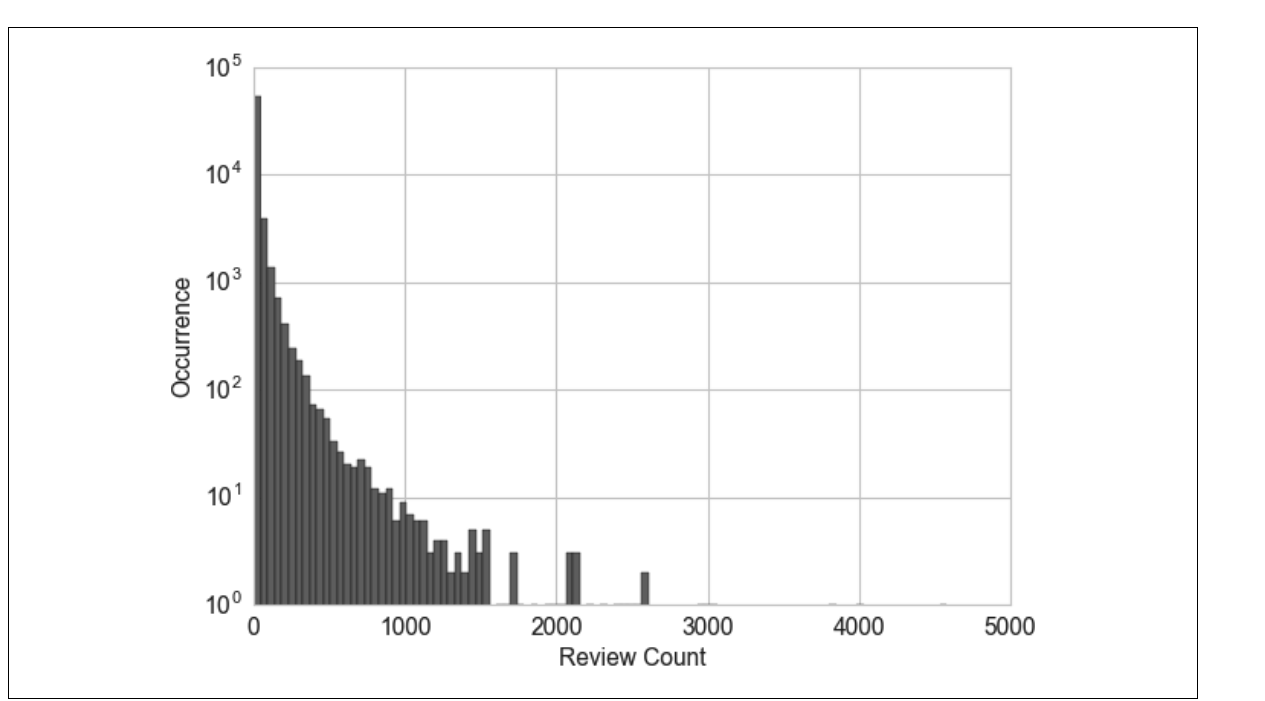
 　　如果用上述数据直接作为协同过滤算法的输入,数据向量某个元素中过大的计数值对相似度的影响会远超其他元素,从而破坏整体的相似度测量.区间量化(分箱)可以将连续型数值映射为离散型数值,我们可以将这种离散型数值看作一种有序的分箱序列,它表示的是对密度的测量。(连续数据的离散化过程)根据系确定箱子大小的方法可以分为自适应分箱以及固定宽度分箱.固定分箱其实也用过,比如把连续的年龄数据离散为年龄段,比如70后,80后之类的.固定分箱的最大缺点在于计数值之间有较大缺口的话会产生较多的空箱.分位数分箱法将数据分为相等的若干分.

　　对数变换(利用Log函数对数据进行压缩),对数变换对处理重尾分布有着不错的效果,利用对数变换处理yelp数据的效果对比如下:

 

 

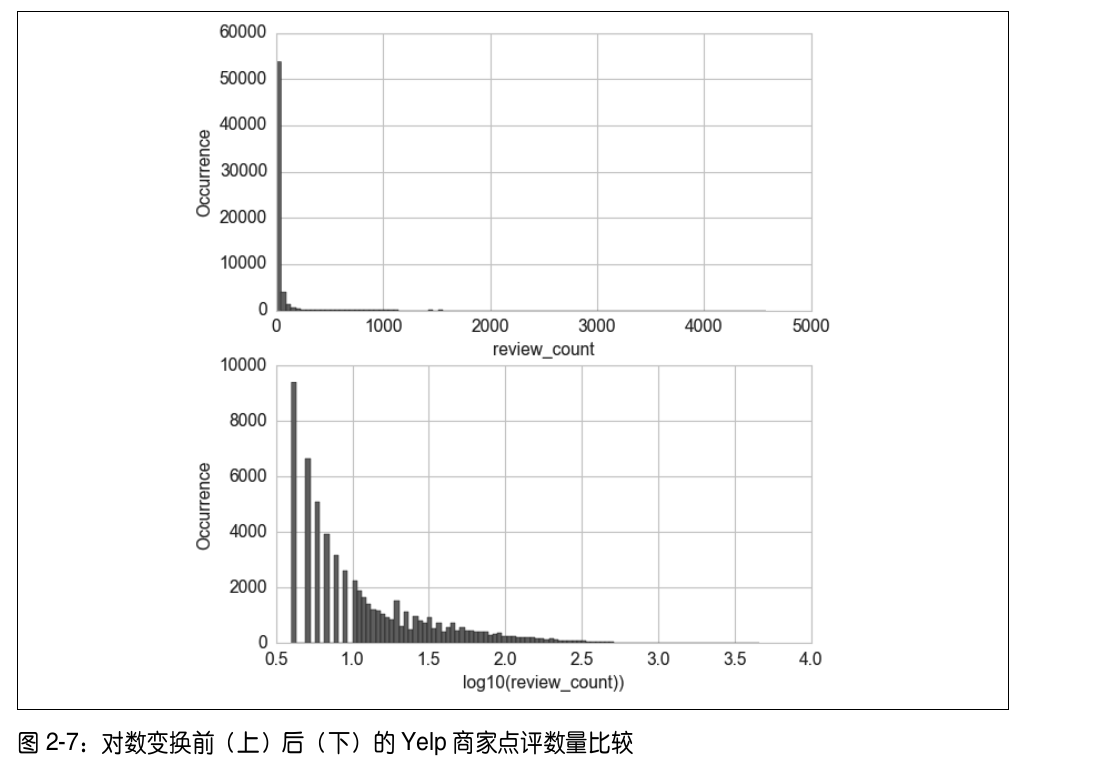
　　经过对数变换之后,直方图在低计数值的集中趋势被减弱了,在 x 轴上的分布更均匀了一些。(在构建模型之初,用数据可视化查看输入输出以及各个特征之间的关系能给出一个比较直观的理解,例如能不能用线性模型来实现一个比较好的拟合效果).

　　指数变化:指数变化是一个变换族,对数变化只是其中的一个特例,该类方法在统计学中称为方差稳定化变化,也成为box-cos变化.详细的box-cos变化见https://wenku.baidu.com/view/96140c8376a20029bd642de3.html,下图截自上述链接.

 

 

 　　box-cox的最有lamda计算方法通过MLE的方法求出,详细的描述在上述提到的链接中,scipy中有box-cox的实现,box-cox变化以及log变化在yelp上的效果对比如下:

　　

 

 box-cox插一个图: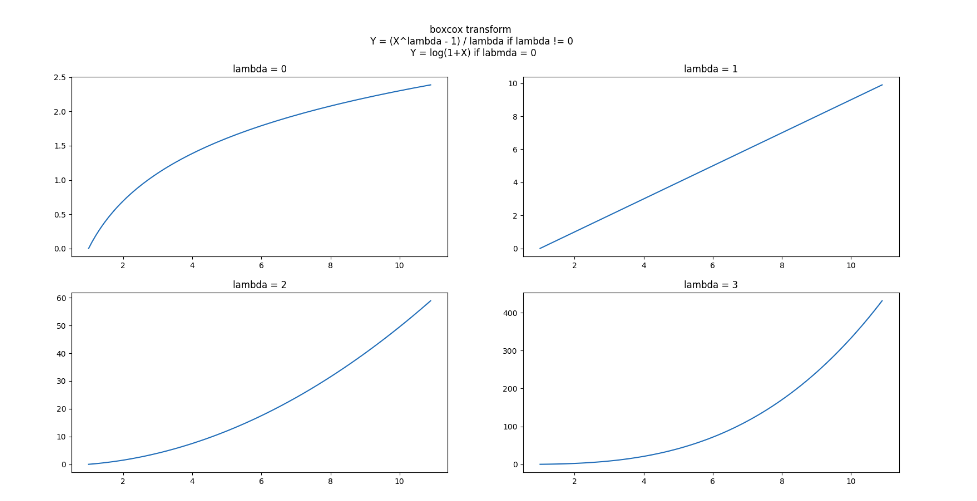

 

 

　　上图lambda取不同值时, (X,Y)的曲线, box-cox变换的工作原理就在这些曲线的斜率中: 曲线斜率越大的区域,则对应区域的X变换后将被拉伸, 变换后这段区域的方差加大; 曲线斜率越小的区域, 对应区域的X变换后将被压缩, 变换后这段区域的方差变小.
　　上图中看出lambda = 0时, 取值较小的部分被拉伸, 取值较大的部分被压缩; lambda > 1时则相反. 所以boxcox变换的应用必须先分析输入X的分布是哪一种偏斜: X分布左偏,则应该应用lambda = 0的变换; X分布又偏,则应该应用lambda > 1的变换.

 

 　　特征缩放 / 归一化

　　有些模型对输入数据的规模比较敏感(比如线性回归模型,逻辑回归模型),基于树的模型(例如决策树)对数据的尺度并不敏感,对于对输入比较的模型而言特征缩放就很重要了.min-max如下图所示:

　

 

 

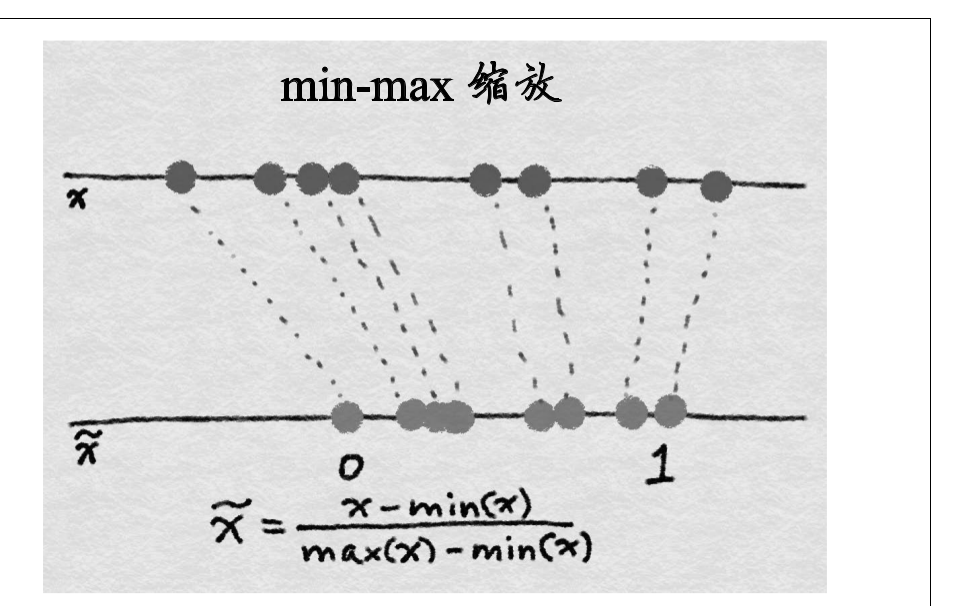
 　　特征标准化缩放如下所示:

　　

 

 

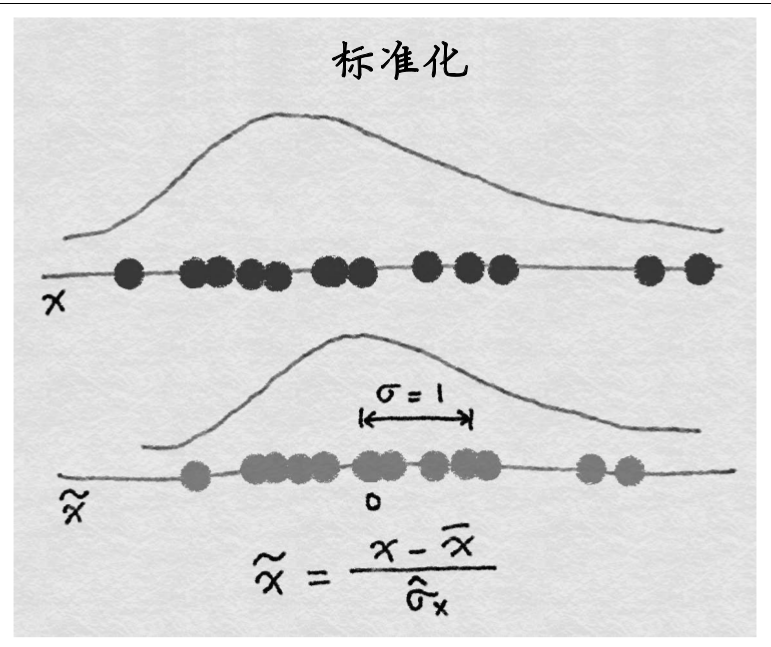
　　hint:在稀疏数据上min-max 缩放和标准化时要注意,min-max 缩放和标准化都是对所有的向量有一个平移的操作(min-max平移min,标准化平移均值).如果平移量不是 0,那么这两种变换会将一个多数元素为 0 的稀疏特征向量变成密集特征向量

 　　$l^2$归一化:$l^2$为欧几里得范数(取模),其先对所有数据点中该特征的值的平方求和.变换示意图如下所示:

　　

 

 

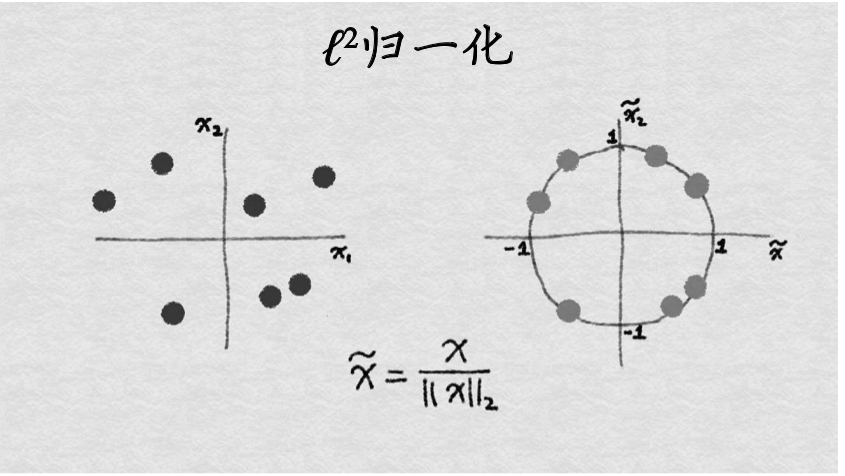
 　　不论使用何种缩放方法,特征缩放总是将特征除以一个常数(称为归一化常数)。因此,它不会改变单特征分布的形状.

　　交互特征:不同特征组合形成一个新的特征(kiggle中用的很常见的一个手法)

　　特征选择:

　　>>过滤:对特征进行预处理,人工的筛去一部分不太可能对模型有用处的特征.例如,我们可以计算出每个特征与响应变量之间的相关性或互信息,然后过滤掉那些在某个阈值之下的特征.(通过相关性来评判特征也是一个比较好的方法)

　　>>打包方法:打包方法将模型视为一个能对推荐的特征子集给出合理评分的黑盒子。它们使用另外一种方法迭代地对特征子集进行优化。(个人理解是通过其他的方法采用类似枚举的方式来对特征的字集进行评判)

　　>>嵌入式方法:将特征选择作为模型训练的一部分.例如决策树的训练过程就是一个特征选择的过程,l1正则化在训练中其的作用也是鼓励模型使用更少的特征.