论文笔记: Matrix Factorization Techniques For Recommender Systems

Recommender system strategies

　　通过例子简单介绍了一下 collaborative filtering 以及latent model,这两个方法在之前的博客里面介绍过,不累述.

Matrix factorization methods 

　　许多成功的LFM都是基于MF的.推荐系统的输入数据需要一定显示反馈信息,例如一个用户给电影的评论.通常包含反馈信息的矩阵都是稀疏的,因为用户不会对所有的电影都作出点评.显示反馈信息并不是一直有效的,推荐系统往往需要使用一些隐式的反馈(例如用户的浏览行为,点击行为)来协助作出一些推断.加入了隐性反馈的矩阵往往是很稠密的,需要很大的空间,矩阵分解在这里就能派上用场了.

A BASIC MATRIX FACTORIZATION MODEL 

　　这部分内容在阅读项亮的<<推荐系统实践>>提及过,在此不重复记录.　

　　论文中提到了两个学习算法,分别是随机梯度下降(Stochastic gradient descent )以及交替最小二乘法(Alternating least squares ),这里简单记录一下ALS.

　　输入:损失函数f(x,y),这里f(x,y)

　　输出:x,y的最优解

　　流程:

　　(1) 随机初始化x

　　(2) 求损失函数f关于y的导数,令其为零获取y的一个当前情况下的最优值$y^*$

　　(3) 用(2)求得的$y^*$固定y,求f关于x的导数,令其为零获取x的一个当前情况下的最优值$x^*$

　　(4) 用(3)求得的$x^*$固定x,重复(2),(3),(4)直到收敛

　　SGD和ALS的一个对比:SGD通常(对于数据集合不大的情况?)比ALS更容易实现也更快的收敛,ALS在以下两种情况下是有效的,一是可以并行计算的系统,二是训练的数据集合不是稀疏数据的情况.SGD需要遍历所有的训练数据集,当训练集变得很大的时候,SGD就变的不切实际了.

ADDING BIASES

　　$\hat{r_{ui}} = q_{i}^T*p_u$获取的是user和item之间互相相互的关系(可以理解为边的联系),并没有考虑到用户和物品本身固有的价值.因此这里要加上一些bias来表示一些固有的信息,这部分在推荐系统实践笔记(八)记录过,不累述.记录一下优化的公式:

　　

 

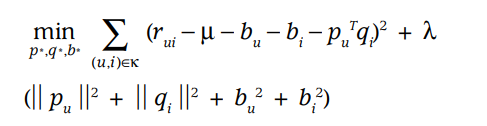
ADDITIONAL INPUT SOURC　　

　　这部分讨论解决冷启动问题.论文中通过添加一些额外的信息来解决冷启动问题.文章主要提到两个属性.

　　> 第一个属性为用户没有明确表明喜欢的数据集.定义物品集合N(u)为用户隐式偏好的项目集,$x_i$为物品i对应的特征,那么用户对N(u)的关注度可以表示为:$\sum_{i{\in}N(u)} x_i$,通常需要需要对求和归一化

　　> 第二个属性为用户个人的属性,比如人口统计学的一些数据,定义A(u)为用户u对应的属性集合,$y_a$为每个属性对应的权重.一个用户的个人属性可以表示为:$\sum_{a{\in}A(u)}y_a$

　　添加了上述两个信息之后的预测公式为:

TEMPORAL DYNAMICS 

 　　引入时间的因素,在前面<<推荐系统实践笔记中>>有对于时间因素的描述,这里不重复描述,公式如下:

INPUTS WITH VARYING CONFIDENCE LEVELS 

　　每个反馈的权重不应该是一样的,引入置信水平可以表示一个行为的频率(原始的反馈是一个简单的二进制,有或者没有),论文用$C_{ui}$来描述$r_{ui}$的置信度水平,改进后的公式如下所示: