推荐系统实践笔记(八)
第八章 评分预测问题
一个评分记录为一个三元组(u,i,r)我们用$r{ui}$表示一个用户u给物品i的评分.
8.2 评分评测算法
(1) 平均值
假设有两个分类的函数,一个是用户分类函数$\phi$,一个是物品分类函数$\varphi$.$\phi(u)$定义了用户u所属的类,$varphi(i)$定义了物品i所属的类,评分预测值为:

(2) 基于领域的方法
基于用户的领域算法认为一个用户对一个物品的评分,需要参考和这个用户兴趣相似的用户对该物品的评分.
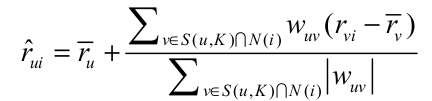
这里, S(u, K) 是和用户 u 兴趣最相似的 K 个用户的集合,N(i) 是对物品 i 评过分的用户集合.$r_{ui}$是用户v对物品i的评价,$\hat{r_v)}$是用户v所有评分的平均值,用户之间的相似度可以通过皮尔逊系数计算:
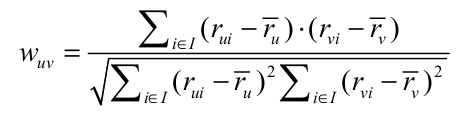
(3) 隐语义模型与矩阵分解模型
用户的评分行为可以表示成一个评分矩阵 R,其中 R [ u ][ i ] 就是用户 u 对物品 i 的评分,评分系统在某种意义上是对矩阵中确实的值填空.要寻找的补全方法是一种对矩阵扰动最小的补全方法--既补充之前与之后矩阵的特征值相差不大.
最开始使用SVD(奇异值分解)来解决这个问题,SVD对空间的要求以及其计算所需的高额时间负责度是大型推荐系统所不能接受的.Funk-SVD用了隐模型的方法来改进SVD,用机器学习训练的方式去获取矩阵(也就是LFM),这部分在第三章有详细的说明.
加入偏置项的LFM
无论是用户还是物品,都有其各自的固定属性,这里用对应的偏置值来表述,改进后的LFM预测公式为:$\hat{r_{ui}} = \mu+b_u+b_i+p_{u}^T*q_i$.新增的三项功能如下:(会有其可解释性)
> $\mu$ 训练集中所有记录的评分的全局平均数,可以用来表示网站本身对用户评分的影响
> $b_u$ 用户偏置项,用来表示用户的固定属性
> $b_i$ 物品偏置项,用来表示物品的固定属性
这个模型称为biasSVD模型
考虑领域影响的LFM
上述的LFM模型并没有显示的考虑用户的历史行为对用户评分测试的影响.首先修改itemCF,让其变为一个可学习的模型,itemCF预测的方式修改如下:
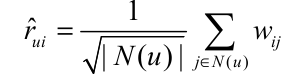
这里,$w_{ij}$不在是相似矩阵,而是有待学习的参数,学习的loss函数为:

这样改进还不够,w是一个比较稠密的矩阵,对空间的要求比较高.koren将w矩阵进行分解,将参数个数降低到2*n*f个,模型如下;
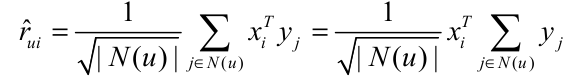
$x_i$与$x_j$为两个F维的向量,用$x_{i}^Tx_j$代替了$w_{ij}$大大降低了参数的数量和存储空间.改进后的模型如下所示:
![]()
加入时间信息
1. 基于领域的模型融合时间信息
主要描述基于物品的领域模型,称为TItemCF,预测公式如下:
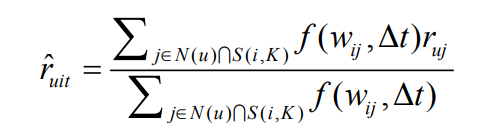
$f(w_{ij},\Delta{t})$是一个考虑了时间衰减的相似函数,$w_{ij}$表示两个物品的相似度,$\Delta{t}$是时间差,主要的目的是提高用户最近的评分行为对推荐系统的影响,f公式如下:

$\sigma(x)$为sigmoid函数,随着$\Delta{t}$增加,$f(w_{ij},\Delta{t})$会变小,也就是用户的行为对现在评测的影响随着时间变长而不那么重要.
2. 基于矩阵分解的模型融合时间信息
引入时间信息后,用户评分矩阵不再是一个二维的矩阵,而是三维矩阵,可以仿照二维矩阵的分解方式对三维矩阵进行分解,biasSVD中新增加的三个部分可以看做对二维矩阵的零维,一维分解.仿照这个思想,我们可以将用户—物品—时间三维矩阵如下分解:
![]()
这里$b_t$建模了系统整体平均分随时间变化的效应,$x_{u}^Ty_t$建模了用户平均分随时间变化的效应,$s_{i}^Tz_t$了用户平均分随时间变化的,公式最后一项建模了用户兴趣随着时间影响的效应.
3. 模型融合
(1) 模型级联融合 (类似adaboost)
和加性模型类似,假设已经有一个模型$\hat{r^k}$,$r_{ui}$为真实的数据,那么类似前向分布算法我们可以定义一个loss如下:
![]()
具体的过程类似adaboost,每次通过上述损失函数设计出一个新的模型,然后在一定参数的限制下加入原有的模型.
(2) 模型加权融合
带权的线性融合:
![]()
一般来说,评分预测问题的解决需要在训练集上训练K个不同的预测器,然后在测试集上作出预测。但是,如果我们继续在训练集上融合K个预测器,得到线性加权系数,就会造成过拟合问题.采用以下三步来解决这个问题:
> 假设数据集已经被分为了训练集A和测试集B,那么首先需要将训练集A按照相同的分割方法分为A1和A2,其中A2的生成方法和B的生成方法一致,且大小相似。
> 在A1上训练K个不同的预测器,在A2上作出预测。因为我们知道A2上的真实评分值,所以可以在A2上利用最小二乘法计算出线性融合系数$\alpha_k$。
> 在A上训练K个不同的预测器,在B上作出预测,并且将这K个预测器在B上的预测结果按照已经得到的线性融合系数加权融合,以得到最终的预测结果。





