论文笔记 XGBoost: A Scalable Tree Boosting System
(2020.4.9)再次阅读的时候,大致梳理了一下行文的思路。
- Xgb原始论文先介绍了其损失函数,(2020.4.21跟进)损失函数用来指导每颗树的生成,也就是决定了在给定数据情况下,叶子节点的最优分裂方式。
- 其次是如果更新CART树的结构(也就是特征的划分方式),论文提出了一个基于贪心策略的特征划分方法以及近似估计特征分裂点的方法,也是文章的亮点之一
XGBoost是boosting算法的其中一种。Boosting算法的思想是将许多弱分类器集成在一起形成一个强分类器,其更关注与降低基模型的偏差。XGBoost是一种提升树模型(Gradient boost machine),其将许多树模型集成在一起,形成一个很强的分类器。而所用到的树模型则是CART回归树模型。讲解其原理前,先讲解一下CART回归树。
一、CART回归树
CART回归树中定义树为二叉树,通过GINI增益函数选定最优划分属性。由于CART为二叉树,与其他决策树相比其在选择了最优分类特征之后,还需要选择一个最优的特征值划分点。比如当前树结点是基于第j个特征值进行分裂的,设该特征值小于s的样本划分为左子树,大于s的样本划分为右子树。
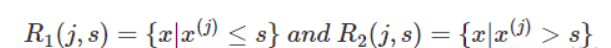
CART回归树实质上就是在该特征维度对样本空间进行划分,而这种空间划分的优化是一种NP难问题,因此,在决策树模型中是使用启发式方法解决。典型CART回归树产生的目标函数为:
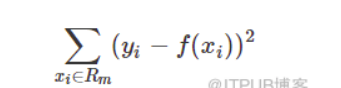
因此,当我们为了求解最优的切分特征j和最优的切分点s,就转化为求解这么一个目标函数:
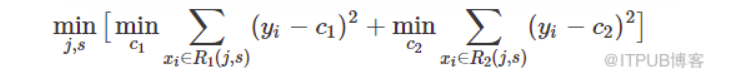
所以我们只要遍历所有特征的的所有切分点,就能找到最优的切分特征和切分点。最终得到一棵回归树。
二、XGBoost基本思想
XGBoost的核心思想与GBM一致,其在实现的过程中通过不断地添加新的树(基模型),不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数,用来拟合上次预测的伪残差。当我们训练完成得到k棵树,我们要预测一个样本的分数,其实就是根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数,最后只需要将每棵树对应的分数加起来就是该样本的预测值。
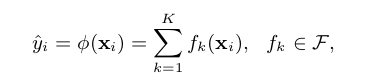
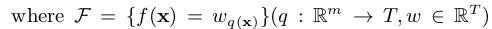
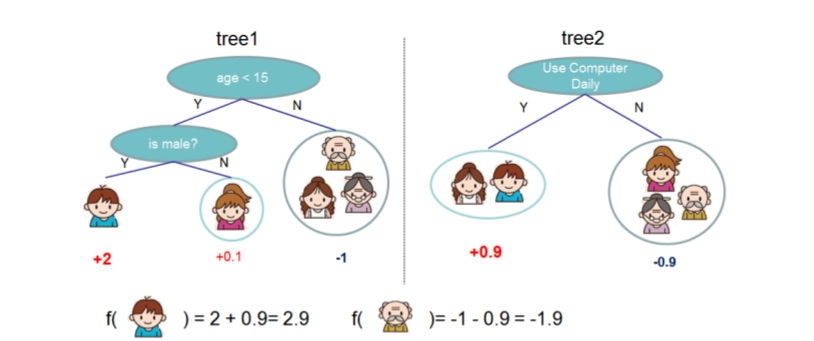
其中q(x)对应的是CART的结构,简单来说指的是x在某一个CART树叶子节点的位置信息.$W_{q(x)}$表示输入x对于某棵CART树的分数。T是树中叶子节点的个数,每个$\mathrm{f}_k(x_i)$对于的是一个CART树,由树的结构q以及叶子节点值W确定。如下图例子,训练出了2棵决策树,小孩的预测分数就是两棵树中小孩所落到的结点的分数相加。爷爷的预测分数同理。
三、XGBoost原理
了解一个学习器,主要是要去理解其损失函数,XGBoost损失函数定义为:
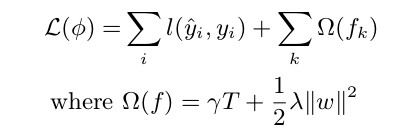
其中第一项为常规损失函数,第二项目为正则项目,用来限制模型的复杂度,降低过拟合的风险。正则化项同样包含两部分,T表示叶子结点的个数,w表示叶子节点的分数。γ、λ为参数分别控制CART树的个数、叶子节点的分数值。
XGBoost采用的也是加性模型的方式,形式化之后的损失函数如下图所示:
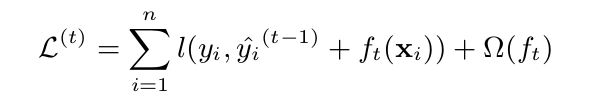
对于表达形式比较复杂,不易理解的函数我们可以尝试使用泰勒展开的技巧,注意到$f_t(xi)$对于的是泰勒展开的$\Delta{x}$项(泰勒展开不清楚的话em....),展开之后的损失函数如下所示:
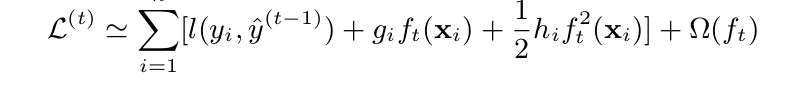
其中$g_i$为$l(y_i,\widetilde{y}^{t-1})$的一阶导,$h_i$为其二阶导。由于前t-1棵树的预测分数与y的残差为常数,对目标函数优化不影响,可以直接去掉。简化目标函数为:
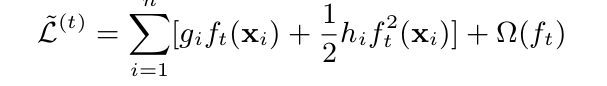
我们定义$I_j = (i|q(x_i) =j)$,$I_j$表示叶子节点对应的输入实例集合,将损失函数项展开之后得到:
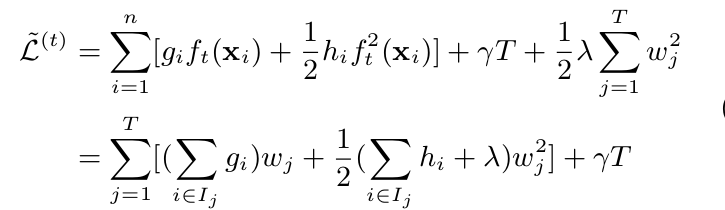
这里简单的解释一下,$\sum_{t=1}^ng_if_t(x_i)$与$\sum_{j=1}^T\sum_{i\in{I_j}}g_iw_j$是等价的,前者求的是所有实例对应在各个CART树中分数的加权和(注意T指代的是叶子节点的个数别搞混淆了),后者也是如此,不过为了合并公式,换了一种表示方式罢了。对上述损失函数求导得:
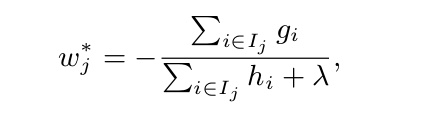
回代之后得到最优情况的表达式,也是XGboost中的用来评估一颗CART数的标准函数:
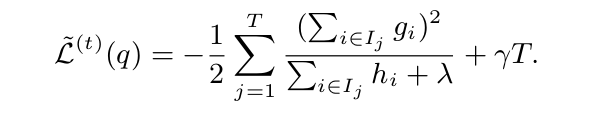
我们记$\sum_{i\in{I}}gi = G$,$\sum_{i\in{I}}h_i = H$则上式可表述为:
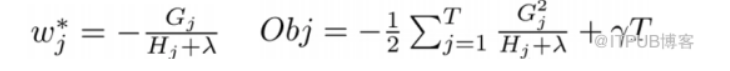
文中还提到了Shrinkage以及subsample技术,Shrinkage与学习率衰减类似,随着迭代次数的增加基函数的权值不断减少,目的是减少每颗树的影响给后续的基函数留够空间,提高模型的robust。subsample在后续记录RF的时候在细说吧。
四、分裂结点算法
在上述推导过程中,我们明确了在清晰的知道一颗树的结构之后,如何求得每个叶子结点的分数。但我们还没介绍如何确定树结构,即每次特征分裂怎么寻找最佳特征,怎么寻找最佳分裂点。基于空间切分去构造一颗决策树是一个NP难问题,我们不可能去遍历所有树结构,因此,XGBoost使用了和CART回归树一样的想法,利用贪婪算法,遍历所有特征的所有特征划分点,不同的是使用上式目标函数值作为评价函数。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益,同时为了限制树生长过深,还加了个阈值,只有当增益大于该阈值才进行分裂。同时可以设置树的最大深度、当样本权重和小于设定阈值时停止生长去防止过拟合。论文中提到了一个贪心选择分裂的算法,具体的做法是预先对特征值进行排序,这样一次遍历过程中通过对前缀和以及后缀和的计算便可以覆盖所有的情况,算法流程如图所示:

五、近似算法
对于连续型特征值,当样本数量非常大,该特征取值过多时,遍历所有取值会花费很多时间,且容易过拟合。因此XGBoost思想是先根据求得的特征权重(feature_importance 根据gini增益指数算出来的)对特征排序获取一些分裂候选点,之后根据候选点对特征进行分桶,即找到l个划分点,将位于相邻分位点之间的样本分在一个桶中。在遍历该特征的时候,只需要遍历各个分位点,从而计算最优划分。从算法伪代码中该流程还可以分为两种,全局的近似是在新生成一棵树之前就对各个特征计算分位点并划分样本,之后在每次分裂过程中都采用近似划分,而局部近似就是在具体的某一次分裂节点的过程中采用近似算法。

六、按权分位算法(weighted quantile sketch)
如何选取近似划分候选点?10000个样本取10个的话,每1000个样本计算一次split value看似可行,其实是不可取的,我们要均分的是loss,而不是样本的数量,而每个样本对loss的贡献可能是不一样的,按样本均分会导致loss分布不均匀,取到的分位点会有偏差。论文中定义了一个rank函数:
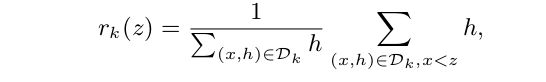
$\mathrm{D}_k =\{(x_1k,h_1),...(x_nk,h_n)\}$rank(z)指的是一个特征的特征值集合中,特征值x小于z的样本中二阶导之和所在总样本二阶导和的比例,也就是用二阶导占比例加权。(2020.3.4)加一些解释,首先给一个公式:
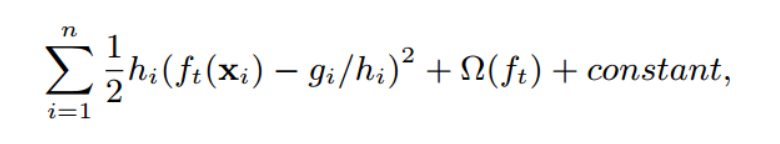
这个公式是和损失函数等价的,前面$h_{i}$就是某个样本的二阶导,后面$g_{i} / h_{i}$是个常数,所以$h_{i}$也就是二阶导可以看做计算残差时某个样本的重要性。因为我们每个节点,要均分的是loss,而不是样本的数量,而每个样本对loss的贡献可能是不一样的,按样本均分会导致loss分布不均匀,取到的分位点会有偏差。加上权重,就能够避免在候选区间里面重要性高的节点扎堆,类似于下图:

ok,继续~论文通过定义这个rank函数用来选取候选的分割点:
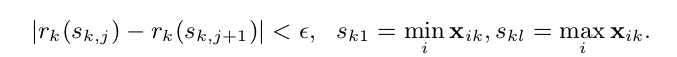
接下来我们对原始的损失函数进行改写:
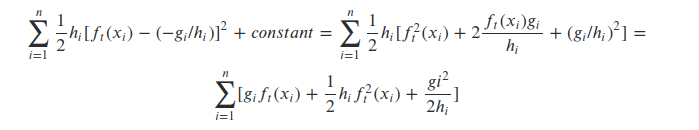
通过这个函数大致解释了解释了为什么用二阶导$h_i$作为权重是合理的。关于这个算法的证明我并没有仔细的去看附录的证明,论文中的符号是有一点问题的,参照别人的探讨以及自己的推论做了一点修改,到目前位置我的理解是这个算法是一种能够给定权重情况下,寻找候选分桶点的算法。算法图也先不贴了,看后面怎么理解。
七、针对稀疏数据的算法(缺失值处理)
当样本的第i个特征值缺失时,无法利用该特征进行划分时,XGBoost的作法不是采取取周围特征值平均值的平滑方式,而是将该样本分别划分到左结点和右结点,然后计算其增益,哪个大就划分到哪边。从而确定一个默认的划分方向。也就是说当特征值不可取或者确实的时候,XGBoost会训练出一个合适的默认划分方式,如下图所示:
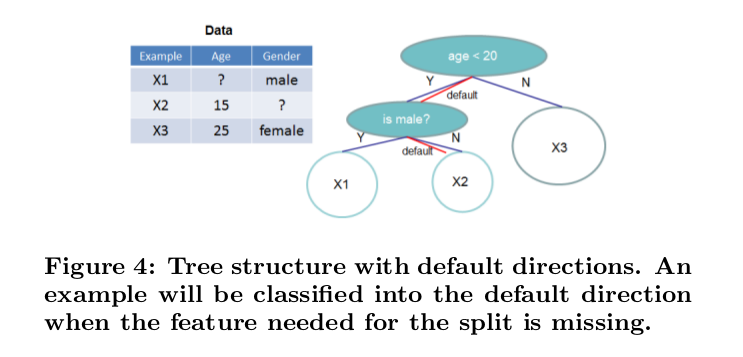
具体的算法流程如下所示:

八、分块并行
在建树的过程中,XGBoost开销最大的部分在每一层选择最优点的过程中,论文中提到的选择最优点的两个算法都需要对数据进行排序,如此多的排序过程是有一些冗余的,论文设计了一个Column Block的数据结构,数据结构存储了每个block中存储了一个特征对应的一个特征值,如果预先对特征值排序,那么排序的开销就可以节省下来。(空间换时间了,想起了acm摸鱼的时候常用的数据预处理打表.....)。使用了Columu Block结构之后,在选择分裂点的算法中,我们可以开CPU多核对多个叶子节点的最优分裂点进行并行计算(选择最优分裂点需要的就是排序好了的特征值以及 feature_importance,这两个都能够在预处理的过程中预先算出来),这样对Block进行一次扫描就可以获取所有叶子节点的分裂情况。Block中的特征还需要存储指向对应样本的index,这样算法实现的过程中才能对特征的指来获取对应计算的梯度。如下图所示:
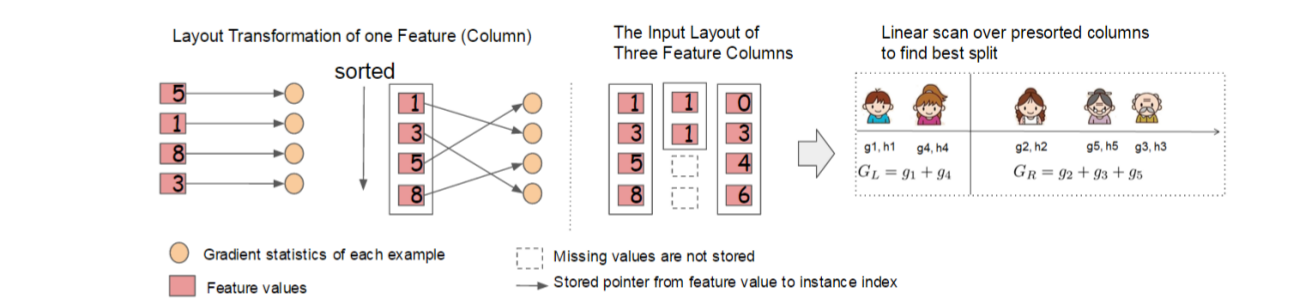
对于approximate算法而言,Xgboost使用了多个Block,存在多个机器上或者磁盘中。每个Block对应原来数据的子集。不同的Block可以在不同的机器上计算。该方法对Local策略尤其有效,因为Local策略每次分支都重新生成候选切分点。Block结构还有其它好处,数据按列存储,可以同时访问所有的列,很容易实现并行的寻找分裂点算法。缺点是空间消耗大了一倍。时间复杂度的分析不难理解我就偷个懒不再这里多说了。
九、缓存优化
这里涉及到一点点os的内容,也不是很多不清楚cache机制的简单百度一下就可以了。使用Block结构的一个缺点是取梯度的时候,是通过索引来获取的,而这些梯度的获取顺序是按照特征的大小顺序的。这将导致非连续的内存访问,可能使得CPU cache缓存命中率低,从而影响算法效率。如下图所示:

因此,对于exact greedy算法中, 使用缓存预取(cache-aware prefetching)。具体来说,对每个线程分配一个连续的buffer,读取梯度信息并存入Buffer中(这样就实现了非连续到连续的转化),然后再统计梯度信息。该方式在训练样本数大的时候特别有用,如下图所示:
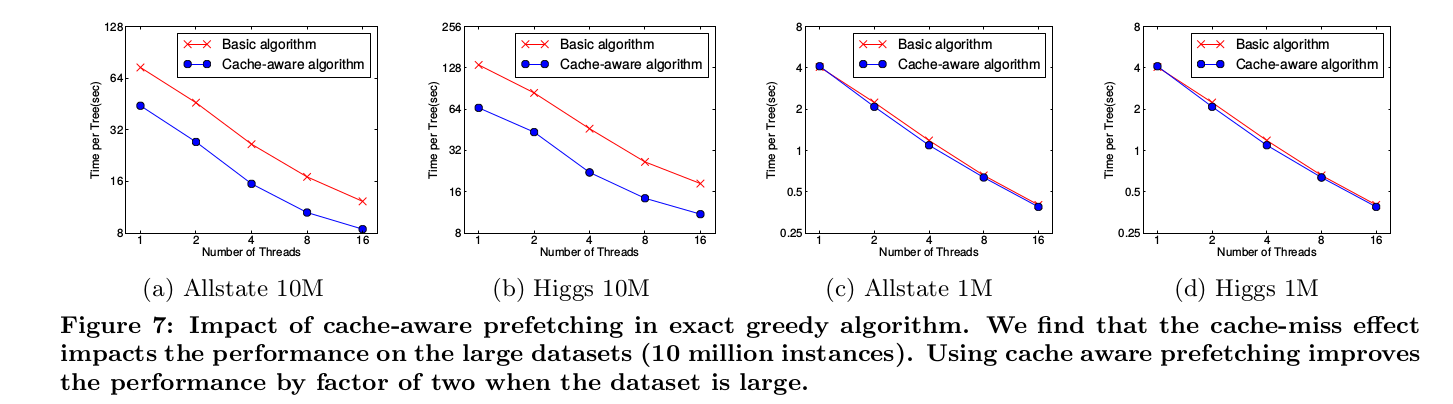
可以看到,对于大规模数据,效果十分明显。在approximate 算法中,对Block的大小进行了合理的设置。定义Block的大小为Block中最多的样本数。设置合适的大小是很重要的,设置过大则容易导致命中率低,过小则容易导致并行化效率不高。经过实验,发现2^16比较好。如下图:
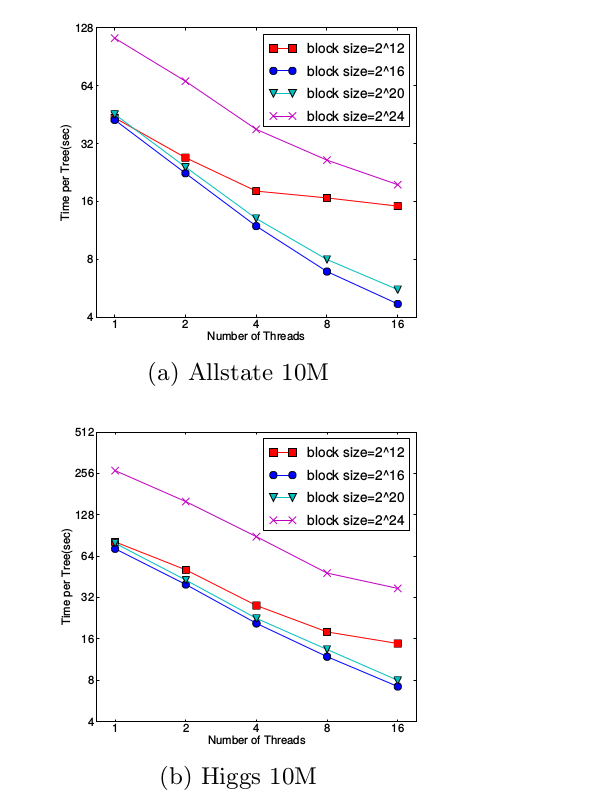
Reference:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号