极限

极限的基本概念

数列极限

定义

如果对于任意给定的 $\varepsilon>0$ ,总存在正整数 $N$ ,当 $n>N$ 时,恒有$\mid x_n-a \mid < \varepsilon$ 成立,则称常数 $a$ 为数列 $\{x_n\}$ 当 $n$ 趋近于无穷时的极限,记为 $\lim\limits_{n \to \infty}x_n=a$或 $x_n\rarr a(n \rarr \infty)$ .

对于定义的进一步理解:

$\varepsilon$ 是用来刻画 $x_n$ 与 $a$ 的接近程度,$N$ 用来刻画 $n \rarr \infty$ 这个极限过程

$\lim\limits_{n \to \infty}x_n=a$的几何意义是:对于 $a$ 点的任何 $\varepsilon$ 领域,一定存在 $N$ ,当 $n>N$ 时,所有的 $x_n$ 都落在该 $\varepsilon$ 区间内,并且只有有限个在这个区间外.

数列 $\{x_n\}$ 的极限是否存在,以及如果存在该极限值等于多少均与数列的前有限项无关.

性质

定理一(极限的唯一性): 如果数列 $\{x_n\}$ 收敛,那么它的极限唯一
定理二(收敛数列的有界性): 如果数列 $\{x_n\}$ 收敛,那么数列 $\{x_n\}$ 一定有界
定理三(收敛数列的保号性): 如果 $\lim\limits_{n \to \infty}=a$ ,且 $a>0$ (或 $a<0$ ),那么存在正整数 $N$ ,当 $n>N$ 时,都有 $x_n>0$ (或 $x_n<0$ )
- 推论: 如果数列 $\{ x_n \}$ 从某项起有 $x_n \geqslant0$ (或 $x_n \leqslant 0$ ),且 $\lim\limits_{n \to \infty}x_n=a$ ,那么 $a \geqslant 0$ (或 $a \leqslant 0$ ).

关于定理三的探究:

为什么定理三中的 $a$ 必须要$>0$,而不是 $\geqslant 0$ ?

如果 $a=0$ ,那么根据数列极限的定义,总存在 $N>0$ , 使得当 $n>N$ 时有 $\mid x_n \mid < \varepsilon$ ,显然此时 $x_n$ 可以落在零点的左侧,这导致"$x_n>0$始终成立"这个结论不成立.

为什么推论中的 $a$ 必须要 $\geqslant0$ ,而不是 $>0$ ?

假设推论中的 $a>0$, 反例: $x_n=\frac{1}{n}$ ,显然对于任意的 $x_n$ 都满足 $x_n\geqslant 0$的条件, 而此时 $\lim\limits_{n \to \infty}x_n=0$ ,可以取到 $0$,与之矛盾.

定理四(收敛数列与其子数列间的关系): 如果数列 $\{x_n\}$ 收敛于 $a$ ,那么它的任一子数列也收敛,且极限也是 $a$ .
- 推论: 如果数列 $\{x_n\}$ 有两个子序列收敛于不同的极限,那么数列 $\{x_n\}$ 必定发散.

常用结论

$\lim\limits_{n \to \infty}x_n=a \iff \lim\limits_{k \to \infty}x_{2k-1}= \lim\limits_{k \to \infty}x_{2k}=a $ (根据收敛数列与其子数列的关系可以推出)
$\lim\limits_{n \to \infty}x_n=a \implies \lim\limits_{n \to \infty} \mid x_n \mid=\mid a \mid$ (根据定义以及绝对值不等式可以推出)
$\lim\limits_{n \to \infty}x_n=0 \iff \lim\limits_{n \to \infty}\mid x_n \mid =0$ (根据定义可以直接推出)
上面两条在函数极限中同样适用

函数极限

定义

自变量趋于有限值时的极限

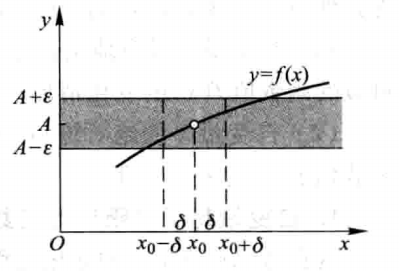
若对任意给定的 $\varepsilon>0$ ,总存在 $\delta>0$ ,当 $0<\mid x- x_0 \mid < \delta$ 时,恒有 $\mid f(x)-A \mid<\varepsilon$ ,则称常数 $A$ 为函数 $f(x)$ 当 $x \to x_0$ 时的极限,记为 $\lim\limits_{x \to x_0}f(x)=A$ .

对定义的进一步理解

$\varepsilon$ 是用来刻画 $f(x)$ 与 $A$ 的接近程度, $\delta$ 是用来刻画 $x \to x_0$ 这个极限过程的

几何意义:对任意给定的 $\varepsilon>0$ ,总存在 $\mathring{U}(x_0, \delta)$ ,当 $x\in \mathring{U}(x_0,\delta)$ 时,曲线 $y=f(x)$ 夹在两直线 $y=A-\varepsilon$ 和 $y=A+\varepsilon$ 之间.

这里 $x \to x_0$ ,但 $x\neq x_0$ .极限 $\lim\limits_{x \to x_0}f(x)$ 是否存在,如果存在极限值等于多少与 $f(x)$ 在 $x=x_0$ 处有没有定义,如果有定义函数值等于多少无关,只与 $x=x_0$ 的去心领域的函数值有关.而要使 $\lim\limits_{x \to x_0}f(x)$ 存在, $f(x)$ 必须在 $x=x_0$ 的某去心领域 $\mathring{U}(x_0,\delta)$ 处处有定义.

若对任意给定的 $\varepsilon>0$ ,总存在 $\delta>0$ ,当 $x_0-\delta<x<x_0$ 时,恒有 $\mid f(x)-A \mid<\varepsilon$ ,则称常数 $A$ 为函数 $f(x)$ 当 $x \to x_0$ 时的左极限,记为

\[\lim\limits_{x \to x_0^-}f(x)=A,或f(x_0^-)=A,或f(x_0-0)=A \]

若对任意给定的 $\varepsilon>0$ ,总存在 $\delta>0$ ,当 $x_0<x<x_0+\delta$ 时,恒有 $\mid f(x)-A \mid<\varepsilon$ ,则称常数 $A$ 为函数 $f(x)$ 当 $x \to x_0$ 时的右极限,记为

\[\lim\limits_{x \to x_0^+}f(x)=A,或f(x_0^+)=A,或f(x_0+0)=A \]

自变量趋近于有限值的极限存在的充要条件:
$\lim\limits_{x \to x_0}f(x)=A \iff \lim\limits_{x \to x_0^+}f(x)=\lim\limits_{x \to x_0^-}f(x)=A$

自变量趋于无穷大时的极限

若对任意给定的 $\varepsilon>0$ ,总存在 $X>0$ ,当 $\mid x\mid>X$ 时,恒有 $\mid f(x)-A \mid < \varepsilon$ ,则称常数 $A$ 为 $f(x)$ 当 $x \to \infty$ 时的极限,记为 $\lim\limits_{x \to \infty}f(x)=A$.

对定义的进一步理解

$\varepsilon$ 是用来刻画 $f(x)$ 与 $A$ 的接近程度, $X$ 是用来刻画 $x \to \infty$ 这个极限过程的

几何意义:对任意给定的 $\varepsilon>0$ ,总存在 $X>0$ ,当 $\mid x \mid >X$ 时,曲线 $y=f(x)$ 夹在两直线 $y=A-\varepsilon$ 和 $y=A+\varepsilon$ 之间.

这里的 $x \to \infty$ 是指 $\mid x \mid \to +\infty$ ;而数列极限中的 $n \to \infty$ 指的是 $n \to +\infty$

若对任意给定的 $\varepsilon>0$ ,总存在 $X>0$ ,当 $ x>X$ 时,恒有 $\mid f(x)-A \mid < \varepsilon$ ,则称常数 $A$ 为 $f(x)$ 当 $x \to +\infty$ 时的极限,记为 $\lim\limits_{x \to +\infty}f(x)=A$.
若对任意给定的 $\varepsilon>0$ ,总存在 $X>0$ ,当 $ x<-X$ 时,恒有 $\mid f(x)-A \mid < \varepsilon$ ,则称常数 $A$ 为 $f(x)$ 当 $x \to -\infty$ 时的极限,记为 $\lim\limits_{x \to -\infty}f(x)=A$.

自变量趋近于无穷的极限存在的充要条件:
$\lim\limits_{x \to \infty}f(x)=A \iff \lim\limits_{x \to +\infty}f(x)=\lim\limits_{x \to - \infty}f(x)=A$

性质

定理一(函数极限的唯一性): 如果 $\lim\limits_{x \to x_0}f(x)$ 存在,那么这个极限唯一
定理二(函数极限的局部有界性): 如果 $\lim\limits_{x \to x_0}f(x)=A$ ,那么存在常数 $M>0$ 和 $\delta>0$ ,使得当 $0<\mid x-x_0 \mid < \delta$ 时,有 $\mid f(x) \mid \leqslant M$.
定理三(函数极限的局部保号性): 如果 $\lim\limits_{x \to x_0}f(x)=A$ ,且 $A>0$(或 $A<0$ ) ,那么存在常数 $\delta>0$ ,使得当 $0< \mid x-x_0 \mid < \delta$ 时,有 $f(x)>0$ (或 $f(x)<0$)

无穷小与无穷大

无穷小

定义

若函数 $f(x)$ 当 $x \to x_0$ (或 $x \to \infty$) 时的极限为零,则称 $f(x)$ 为 $x \to x_0$ (或 $x \to \infty$)时的无穷小量.

极限值与无穷小定理

在自变量的统一变化过程 $x \to x_0$ (或 $x \to \infty$)中,函数 $f(x)$ 具有极限 $A$ 的充分必要条件是 $f(x)=A+\alpha$,其中 $\alpha$ 是无穷小.

\[\lim f(x)=A \iff f(x)=A+\alpha \]

无穷小的比较

设 $\alpha$ 与 $\beta$ 是在同一个自变量变化过程中的无穷小,且 $\alpha \neq 0$.

\[\begin{aligned} &若 \lim \frac{\beta}{\alpha}=0,那么就说\beta是\alpha的高阶无穷小,记作 \beta=\omicron(\alpha)\\ &若 \lim \frac{\beta}{\alpha}=\infty,那么就说\beta是\alpha的低阶无穷小,记作 \alpha=\omicron(\beta)\\ &若 \lim \frac{\beta}{\alpha}=c\neq0,那么就说\beta是\alpha的同阶无穷小,记作 \beta=\Omicron(\alpha)\\ &若 \lim \frac{\beta}{\alpha^k}=c\neq0,那么就说\beta是\alpha的k阶无穷小\\ &若 \lim \frac{\beta}{\alpha}=1,那么就说\beta与\alpha是等价无穷小,记作\alpha \sim \beta\\ \end{aligned} \]

常用等价无穷小

\[\begin{aligned} &x \sim \sin x \sim \tan x \sim \arcsin x \sim \arctan x \sim \ln(1+x) \sim e^x-1,\\ &(1+x)^\alpha-1 \sim \alpha x,1-\cos x \sim \frac{1}{2}x^2,a^x-1\sim x\ln a,\\ &x-\sin x \sim \frac{1}{6}x^3,\tan x -x \sim \frac{1}{3}x^3,x-\ln(1+x) \sim \frac{1}{2}x^2,\\ &\arcsin x - x \sim \frac{1}{6}x^3,x-\arctan x \sim \frac{1}{3}x^3 \end{aligned} \]

无穷小的运算性质

有限个无穷小的和仍是无穷小
有限个无穷小的积仍是无穷小
无穷小量与有界量的积仍是无穷小

无穷大

定义

设函数 $f(x)$ 在 $x_0$ 的某一去心领域内有定义(或 $\mid x \mid $ 大于某一正数时有定义).如果对于任意给定的正数 $M$ (不论它多么大),中存在正数 $\delta$ (或正数 $X$),只要 $x$ 适合不等式 $0<\mid x-x_0 \mid < \delta$ (或 $\mid x \mid>X$),对应的函数值 $f(x)$ 总满足不等式:

\[\mid f(x)\mid>M \]

那么称函数 $f(x)$ 是当 $x\to x_0$(或 $x \to \infty$ )时的无穷大.
虽然按照函数的定义来说, 当$x\to x_0$(或 $x \to \infty$ )时的无穷大的函数 $f(x)$ 极限是不存在的.但是为了便于叙述函数的这一性态,我们也说"函数的极限是无穷大",并记作:

\[\lim\limits_{x \to x_0}f(x)= \infty(或 \lim\limits_{x\to \infty}f(x)=\infty) \]

无穷大的运算性质

有限个无穷大量的积仍为无穷大量
无穷大量与有界变量之和仍为无穷大量
有限个正无穷大量之和一定是无穷大

无穷大与无穷小的关系

在自变量同一变化过程中,如果 $f(x)$ 为无穷大,那么 $\frac{1}{f(x)}$ 为无穷小;反之,如果 $f(x)$ 为无穷小,且 $f(x)\neq0$,那么 $\frac{1}{f(x)}$ 为无穷大.

无穷大和函数无界的辨析

无穷大是函数在自变量某一个变化过程中的变化趋势,而函数无界是函数整体的性质,二者不可混同.
另一方面,我们可以看出:若一个函数在自变量的某一变化过程中极限为无穷大,那么这个函数必定为无界函数,但如果一个函数是无界函数,并不可以说明该函数在自变量的某一变化过程中变化趋势为无穷大.即,函数在某一极限过程为无穷大是函数为无界函数的充分非必要条件.

常用无穷大量的比较

当 $x \to +\infty$ 时(函数极限)

\[\ln^{\alpha}x <x^\beta<a^x,其中a>0,\beta>0,a>1 \]

当 $n\to \infty$ 时(数列极限)

\[\ln^\alpha n< n^\beta<a^n<n!<n^n,其中\alpha>0,\beta>0,a>1 \]

极限运算法则

无穷小与无穷大相关运算法则

无穷小的运算性质
 无穷大的运算性质

极限的有理运算法则

如果 $\lim f(x)=A$, $\lim g(x)=B$,那么:

$\lim[f(x)±g(x)]=\lim f(x)± \lim g(x)=A±B$;
$\lim[f(x) \cdot g(x)]=\lim f(x)\cdot \lim g(x)=A \cdot B$;
若又有 $B \neq 0$ ,则

\[\lim \frac{f(x)}{g(x)}=\frac{\lim f(x)}{\lim g(x)}=\frac{A}{B} \]

注意:上面所有的运算法则成立的前提是:$\lim f(x)$与 $\lim g(x)$都存在!

推论:

如果 $\lim f(x)$ 存在,而 $c$ 为常数,那么:

\[\lim[c\cdot f(x)]=c\cdot \lim f(x) \]

如果 $\lim f(x)$ 存在,而 $n$ 是正整数,那么:

\[\lim[f(x)]^n=[\lim f(x)]^n \]

注意:数列极限同样满足

常用的结论

$\lim f(x)=A \neq 0 \implies \lim f(x)g(x)=A\lim g(x)$;

即:极限非零的因子的极限可先求出来.

$\lim \frac{f(x)}{g(x)}存在,\lim g(x)=0 \implies \lim f(x)=0$
$\lim \frac{f(x)}{g(x)}=A\neq 0,\lim f(x)=0 \implies \lim g(x)=0$

复合函数求极限法则

设函数 $y=f[g(x)]$ 是由函数 $u=g(x)$ 与函数 $y=f(u)$ 复合而成,$f[g(x)]$ 在点 $x_0$ 的某去心领域内有定义,若 $\lim\limits_{x \to x_0}g(x)=u_0$ , $\lim\limits_{u \to u_0}f(u)=A$,且存在 $\delta_0>0$,当 $x \in \mathring{U}(x_0, \delta_0)$ 时,有 $g(x)\neq u_0$ ,则:

\[\lim\limits_{x \to x_0}f[g(x)]=\lim\limits_{u \to u_0} f(u)=A \]

为什么一定要有:存在 $\delta_0>0$,当 $x \in \mathring{U}(x_0, \delta_0)$ 时,有 $g(x)\neq u_0$.这一条件?
这是因为函数在某一点的极限实际上与该点的值无关,假设极限$\lim\limits_{x \to x_0}f(x)=A$,如果 $f(x)$ 在$x_0$点没有定义,或是在该$x_0$处间断,并不会影响函数最终在 $x_0$ 处的极限为 $A$.
回到本定理,如果不加上这个条件的话,可能出现在所有可能的领域中都会出现 $g(x)=u_0$ 的情况 ,这会导致在某些情况下 $f[g(x)]$ 在 $x_0$ 点的领域中取到令外层函数 $f(u)$ 没有定义或者间断的点--- $f(u_0)$ , 因为条件中的$\lim\limits_{u \to u_0}f(u)=A$并不能说明 $f(u_0)$ 处的情况,进而导致函数 $ f[g(x)]$在领域内违背极限的定义 $\mid f[g(x)]-A\mid< \varepsilon$.

极限存在准则及两个重要极限

准则零

$\lim\limits_{x \to \infty}f(x)=A \iff \lim\limits_{x \to +\infty}f(x)=\lim\limits_{x \to - \infty}f(x)=A$
$\lim\limits_{x \to x_0}f(x)=A \iff \lim\limits_{x \to x_0^+}f(x)=\lim\limits_{x \to x_0^-}f(x)=A$

准则一(迫敛准则/夹逼准则)

如果数列 $\{x_n\}$,$\{y_n\}$及$\{z_n\}$满足下列条件:

存在 $n_0\in \N_+$,当 $n>n_0$ 时,有 $y_n \leq x_n \leq z_n$;
$\lim\limits_{n \to \infty}y_n=a,\lim\limits_{n \to \infty}z_n=a$.

那么数列$\{x_n\}$的极限存在,且 $\lim\limits_{n \to \infty}x_n=a$

数列极限同理满足,不细述.

根据此准则可以推导出重要极限 $\lim\limits_{x \to x_0}\frac{\sin x}{x}=1$.

准则二(单调有界准则)

单调有界数列必有极限.即:单调增(减)有上(下)界的数列必有极限.

注意:

该准则中的单调数列,区别与函数的单调,是广义上的单调而非严格单调,即若数列 $\{x_n\}$满足:$x_1 \leq x_2 \leq x_3 \leq ... \leq x_n \leq x_{n+1} \leq ... $就称数列 $\{x_n\}$ 是单调增加的.

当一个函数在 $R$ 上单调递增(减)有界,在正无穷远处极限存在,且极限值为上(下)确界.

除了第二点说述的情况,该结论无法推广至其他函数极限,因为在谈及函数极限时往往需要指明定义域与极限的过程,仅仅说明"单调有界函数必有极限"是没有意义的.

使用该准则可以推导出另一个重要极限:$\lim\limits_{x \to \infty}(1+\frac{1}{x})^x$的存在,并且我们把该极限的值定义为 $e$,它是一个无理数.

posted @ 2022-04-05 21:11 smile_zyk 阅读(851) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

smile_zyk

极限