函数

目录

• 概念
  • 函数
    • 定义
  • 复合函数
    • 定义
  • 反函数
    • 定义
  • 初等函数
    • 定义
    • 基本初等函数
      • 幂函数 (\(y=x^{\mu}(\mu为实数)\))
      • 指数函数 (\(y=a^{x}(a>0,a\neq 1)\))
      • 对数函数 (\(y=\log_{a}{x}(a>0,a\neq 1)\) )
      • 三角函数与反三角函数
• 性质
  • 单调性
    • 定义
  • 奇偶性
    • 定义
  • 周期性
    • 定义
  • 有界性
    • 定义

概念

函数

定义

设 \(x\) 和 \(y\) 是两个变量, \(D\) 是一个给定的数集,如果对于每个数 \(x\in D\) ,变量 \(x\) 按照一定的法则总有一个确定的数值 \(y\) 和它对应,则称 \(y\) 是 \(x\) 的函数,记为:

\[y=f(x),x \in D \]

其中 \(x\) 称为自变量 \(y\) 称为因变量, \(D\) 称为函数的定义域,记作 \(D_f\) ,即 \(D_f=D.\)
函数值 \(f(x)\) 的全体所构成的集合称为函数 \(f\) 的值域,记作 \(R_f\) 或 \(f(D)\) ,即

\[R_f=f(D)= \{ y \mid y=f(x),x \in D \} \]

函数的两个基本要素:
定义域,对应规则(或称依赖关系),当两个函数的定义域与对应规则完全相同时,它们就是同一函数

复合函数

定义

设函数 \(y=f(u)\) 的定义域为 \(D_f\) ,函数 \(u=g(x)\) 的定义域为 \(D_g\) ,值域为 \(R_g\) ,若 $D_f\cap R_g \neq \emptyset $ ,则称函数 \(y=f[g(x)]\) 为函数 \(y=f(u)\) 与 \(u=g(x)\) 的复合函数.它的定义域为 \(\{x \mid x \in D_g,g(x)\in D_f\}\).

注意:
根据定义,不是任何两个函数都可以复合,只有满足 $D_f\cap R_g \neq \emptyset $ 的两个函数才可以复合 .

反函数

定义

设函数 \(y=f(x)\) 的定义域为 \(D\) ,值域为 \(R_y\) .若对任意 \(y\in R_y\) ,有唯一确定的 \(x\in D\) 使得 \(y=f(x)\) ,则记为 \(x=f^{-1}(y)\) ,称其为 \(y=f(x)\) 的反函数.

注意:

• 根据定义,不是任何函数都有反函数,只有满足对任意 \(y\in R_y\) ,有唯一确定的 \(x\in D\) 使得 \(y=f(x)\) 的函数才有反函数
• 严格单调函数一定有反函数,反之不成立
• 在同一直角坐标系中 \(y=f(x)\) 与 \(y=f^{-1}(x)\) 关于 \(y=x\) 对称
• \(f^{-1}[f(x)]=x\) , \(f[f^{-1}(x)]=x\) .

初等函数

定义

由常数和基本初等函数经过有限次四则运算和有限次的函数复合所构成并可用一个式子表示的函数,称为初等函数

基本初等函数

将幂函数,指数函数,对数函数,三角函数,反三角函数统称为基本初等函数

幂函数 (\(y=x^{\mu}(\mu为实数)\))

1. 幂函数 \(y=x^{\mu}\) 的定义域和值域取决于 \(\mu\) 的取值,当 \(x>0\) 时, \(y=x^{\mu}\) 都有定义.
2. 常见幂函数:\(y=x,y=x^2,y=x^3,y=\sqrt{x},y=\sqrt[3]{x},y=\frac{1}{x}\).

y=x^2的函数图像

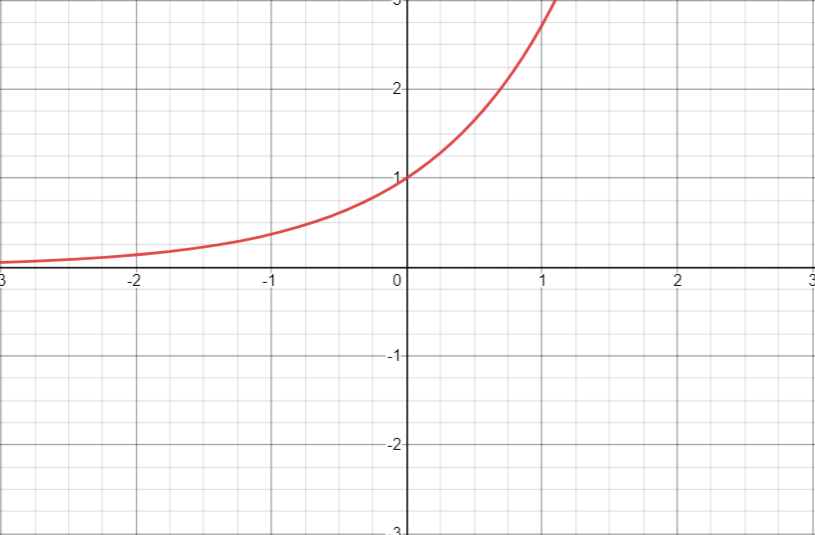
指数函数 (\(y=a^{x}(a>0,a\neq 1)\))

1. 定义域: \((-\infty,+\infty)\),值域: \((0,+\infty)\).
2. 单调性:当 \(a>1\) 时, \(y=a^{x}\) 单调增;当 \(0<a<1\) 时, \(y=a^{x}\) 单调减.
3. 常见指数函数: \(y=e^{x}\)

y=e^x的函数图像

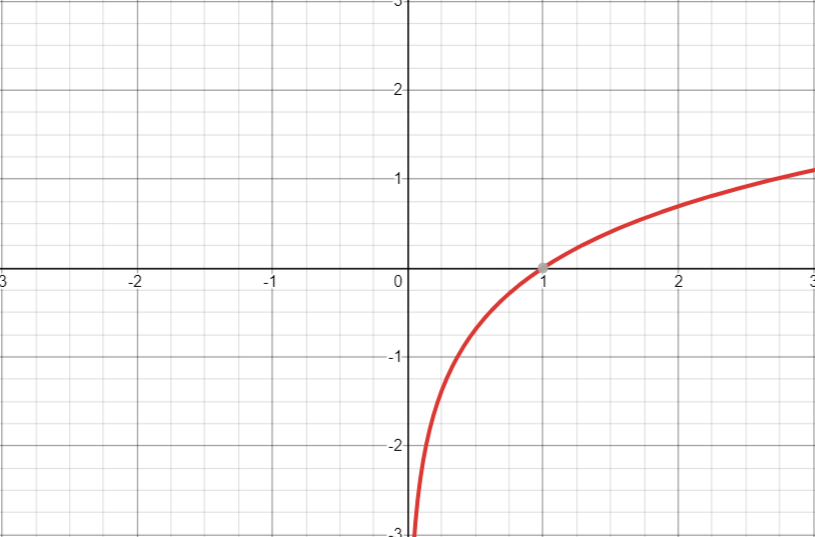
对数函数 (\(y=\log_{a}{x}(a>0,a\neq 1)\) )

1. 定义域:\((0,+\infty)\),值域:\((-\infty,+\infty).\)
2. 单调性:当 \(a>1\) 时, \(y=\log_a{x}\) 单调增;当 \(0<a<1\) ,\(y=\log_a{x}\) 单调减.
3. 常见对数函数:\(y=\ln{x}\)

y=ln x的函数图像

NOTE:指数函数和对数函数互为反函数

三角函数与反三角函数

以下图片来自知乎用户:浣熊数学
链接:三角函数公式需要背下来吗？

性质

单调性

定义

设函数 \(y=f(x)\) 在某区间 \(I\) 上有定义,如果对于区间 \(I\) 上的任意两点 \(x_1<x_2\) 恒有 \(f(x_1)<f(x_2)\) 或( \(f(x_1)>f(x_2)\) ),则称 \(y=f(x)\) 在该区间内单调增加(或单调减少)

注意:函数的单调性可以通过一阶导数的正负进行判定.

奇偶性

定义

设函数 \(y=f(x)\)的定义域 \(D\) 关于原点对称(即若 \(x\in D\) 则有 \(-x \in D\) ),对于任一 \(x \in D\) ,如果恒有:

\[f(-x)=f(x) \]

则称 \(f(x)\) 为 \(D\) 上的偶函数;如果恒有:

\[f(-x)=-f(x) \]

则称 \(f(x)\) 为 \(D\) 上的奇函数

注意:

• 任何一个函数 \(f(x)\) 都可以写成一个奇函数和一个偶函数相加的形式: \(f(x)=\frac{f(x)+f(-x)}{2}+\frac{f(x)-f(-x)}{2}\)
• 奇函数 \(y=f(x)\) 的图像关于原点对称,且若 \(f(x)\) 在 \(x=0\) 处有定义,则 \(f(0)=0\);而偶函数的图像关于 \(y\) 轴对称
• 两个奇(偶)函数之和仍为奇(偶)函数,两个奇(偶)函数值之积必为偶函数,奇函数与偶函数之积必为奇函数.

周期性

定义

若存在实数 \(T>0\) ,对于任意 \(x\) 恒有 \(f(x+T)=f(x)\) ,则称 \(y=f(x)\) 为周期函数.使得上述关系成立的最小正数 \(T\) 称为 \(f(x)\) 的最小正周期,简称为 \(f(x)\) 的周期

注意:

• 若 \(f(x)\) 以 \(T\) 为周期,则 \(f(ax+b)\) 以 \(\frac{T}{\mid a \mid}\) 为周期

有界性

定义

设 \(y=f(x)\) 在集合 \(X\) 上有定义.若存在 \(M>0\) ,使得对任意的 \(x \in X\) ,恒有:

\[\mid f(x) \mid \leqslant M \]

则称 \(f(x)\) 在 \(X\) 上为有界函数,否则称 \(f(x)\) 在 \(X\) 上为无界函数.即:
如果对任意的 \(M>0\) ,至少存在一个 \(x_0 \in X\) 使得:

\[\mid f(x_0)\mid>M \]

则 \(f(x)\) 为 \(X\) 上的无界函数.

注意:区分无界变量与无穷大量