201871010130-周学铭 实验二 个人项目—D{0-1}问题项目报告
| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | 18级卓越班 |
| 这个作业要求链接 | 实验二 软件工程个人项目 |
| 我的课程学习目标 | 掌握软件项目个人开发流程。 掌握Github发布软件项目的操作方法。 |
| 这个作业在哪些方面帮助我实现学习目标 | 首先通过D{0-1}背包的小项目,让我们模拟软件项目个人开发的流程。 其次通过github的使用,让我们掌握发布软件项目的操作方法。 |
| 项目Github的仓库链接地址 | github |
1.任务一:阅读教师博客“常用源代码管理工具与开发工具”内容要求,点评班级博客中已提交相关至少3份作业。
| 评论地址 | 评论内容 |
|---|---|
| 201871030105-陈啟程 | 该博客描述了代码版本管理工具的发展历史,并比较了他们之间的区别;同时还调研了市面上主流的IDE工具,并对它们进行了比较,使我受益良多。但针对博客的排版还需要加强。 |
| 201871030110-何飞 | 该博客,内容精练,排版整齐美观。针对于任务2(IDE的调研)能够精确的把握住不同IDE的优势与不足,并简单扼要地进行介绍;但对于任务1(代码版本管理软件的调研)就显得比较粗略了。 |
| 201871030102-崔红梅 | 该博客针对于每一个不同的代码管理工具与开发工具,分别从不同方面、不同角度进行了详细地描述与介绍,内容充实详尽,相信每一个读到该博客的人都能有所收获。但博客排版较为单一,缺少了层次感,同时如果在内容上面能够将不同的工具画个表格进行分析对比,那么就更加完美了。 |
2.任务二:总结详细阅读《构建之法》第1章、第2章,掌握 PSP流程。
-
《构建之法》第一章总结:该章内容主要解释了两部分内容:软件=程序+软件工程以及软件工程是什么。
-
软件=程序+软件工程:
- 邹欣老师首先通过了一些问题解释了什么是“软件”,什么是“程序”。然后通过了一些通俗的例子,为我们介绍了许多关于软件工程的概念。最后又通过航空产业来和软件开发做对比,讲述了软件开发的不同阶段,并引出了什么是软件工程这个问题。
-
软件工程是什么:邹欣老师通过软件工程的特殊性,软件工程与计算机科学的关系,软件工程的知识领域和软件工程的目标这四个方面来介绍了软件工程是什么。
-
软件工程的特殊性:复杂性,不可见性,易变性,服从性,非连续性。
-
软件工程与计算机科学的关系:
计算机科学 软件工程 发现和研究长期的、客观的真理 短期的实际结构(具体的软件会过时) 理想化的 对各种因素的折衷 确定性,完美,通用性 对不确定性和风险的管理,足够好,具体的应用 各个学科独立深入研究,做出成果 关注和应用各个相关学科的知识,解决问题 统一的理论 百花齐放的实践方法 形式化,追求简明的公式 在实践中建立起来的灵感和直觉 正确性 可靠性 -
软件工程的知识领域:邹欣老师列出了15个知识领域,其中包含12个软件工程学科本身的知识领域以及软件工程的三大类基础知识领域:计算基础,数学基础和工程基础。
-
软件工程的目标:用户满意度,可靠性,软件流程的质量,可维护性。
-
-
-
《构建之法》第二章总结:该章内容主要介绍了PSP(Personal Software Process,个人软件开发流程)。
- 单元测试:一个针对如何能让自己负责的模块功能定义尽量明确,模块内部的改变不会影响其他模块,而且模块的质量能得到稳定的、量化的保证的一个解决方案。
- 好的单元测试标准:
- 单元测试应该在最基本的功能/参数上验证程序的正确性。
- 单元测试必须由最熟悉代码的人(程序的作者)来写。
- 单元测试过后,机器状态保持不变。
- 单元测试要快。
- 单元测试应该产生可重复、一致的结果。
- 独立性。
- 单元测试应该覆盖所有代码路径。
- 单元测试应该集成到自动测试的框架中。
- 单元测试必须和产品代码一起保存和维护。
- 好的单元测试标准:
- 回归测试:
- 回归可以理解为:回归到以前不正常的状态。
- 目的:
- 验证新的代码的确改正了缺陷。
- 同时要验证新的代码有没有破坏模块的现有功能,有没有Regression。
- 效能分析工具:
- 两种分析工具:
- 抽样:指当程序运行时,IDE时不时会看到这个程序在哪一个函数内,并记录下来。程序结束后,IDE就会得出一个关于程序运行时间分布的大致印象。
- 优点:不需要改动程序,运行较快,可以很快找到瓶颈,但是不能得出精确的数据,也不能准确表示代码中的调用关系树。
- 代码注入:指将检测的代码加入到每一个函数中,这样程序的一举一动都被记录在案,程序的各个效能数据都可以被精确地测量。
- 缺点:程序地运行时间大大加长,还会产生很大地数据文件,也相应增加了数据分析的时间。
- 抽样:指当程序运行时,IDE时不时会看到这个程序在哪一个函数内,并记录下来。程序结束后,IDE就会得出一个关于程序运行时间分布的大致印象。
- 两种分析工具:
- 单元测试:一个针对如何能让自己负责的模块功能定义尽量明确,模块内部的改变不会影响其他模块,而且模块的质量能得到稳定的、量化的保证的一个解决方案。
-
PSP流程:
-
软件工程师的任务清单:
PSP2.1 Planning 计划 · Estimate · 明确需求和其他相关因素,指明时间成本和依赖关系 Development 开发 · Analysis · 分析需求 · Design Spec · 生成设计文档 · Design Review · 设计复审 · Coding Standard · 代码规范 · Design · 具体设计 · Coding · 具体编码 · Code Review · 代码复审 · Test · 测试 Record Time Spent 记录用时 Test Report 测试报告 Size Measurement 计算工作量 Postmortem 事后总结 Process Improvement Plan 提出过程改进计划 -
PSP特点:
- 不局限于某一种软件技术,而是着眼于软件开发的流程。
- 不依赖于考试,而主要靠工程师自己收集数据,然后分析,提高。
- 在小型、初创的团队中,很难找到高质量的项目需求,这意味着给程序员的输入质量不高。
- PSP依赖于数据。
- PSP的目的是记录工程师如何实现需求的效率,而不是记录顾客对产品的满意度。
-
3.任务三:个人项目——D{0-1}KP问题。
-
背景知识——0/1背包:
- 基本题意:有N件物品和一个容量为V的背包。第i件物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使价值总和最大。
- 基本思路:特点是:每种物品仅有一件,可以选择放或不放。
- 回溯法:因为对于每种物品仅有选或不选两种操作,所以显然我们可以使用回溯法来进行,即在每一个函数中,调用两个子函数(选中该物品或不选该物品)。但这样的算法时间复杂度为O(2^n),该算法运算效率较低。所以我们必须通过剪枝来减少该算法的运算时间。
- 动态规划法:由于该问题满足最优子结构性质和无后效性,所以该问题可以使用动态规划来解决。
- 状态的表示:
f[i][v]:表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。 - 转移方程:
f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}(c数组表示费用,w数组表示价值)
- 状态的表示:
- 空间优化:
- 方法1(滚动数组):由于最多只有当前物品的前一个物品的状态会对该物品产生影响,所以我们可以通过滚动数组(即i%2)来优化空间复杂度,使得空间复杂度由O(2^n)转变为O(2n)。
- 方法2(根据方法1进一步优化):根据转移方程可得,方程
f[i][v]对他有影响的都是容量小于v的,所以我们只需要将遍历顺序变为容量由大到小,就可以将二维数组变成一维,空间复杂度降为O(N)。
-
背景知识——分组背包:
- 基本题意:有N件物品,告诉你这N件物品的重量以及价值,将这些物品划分为K组,每组中的物品互相冲突,最多选一件,求解将哪些物品装入背包可使这些物品的费用综合不超过背包的容量,且价值总和最大。
- 基本思路:分组背包问题是0-1背包的扩展,我们只需要将将分组背包中的每一个分组看成0-1背包中的一个物品,即可使用0-1背包的算法来实现。同时在算法实现的过程中,再遍历一遍同一个分组中的所有物品即可。
-
D{0-1}KP问题需求分析:
- 数据读入:题目给出的数据包含了许多用来解释的文字,所以在读取数据前要对数据进行清洗,保证读取的数据都是所需要的重量与价值。并且能够将数据进行分组(即转换为上面提到的分组背包模型)。
- 数据可视化:为了直观的展示测试数据的分布,我们需要将数据进行可视化处理。
- 数据的排序:将每一组数据按照第三项的价值:重量比进行排序。
- 求解方式:需要通过动态规划法和回溯法两种方式进行求解。同时为了能让用户自主选择用哪种方式求解,所以还需要设计一个用户界面。
- 数据的存储:将任意一组D{0-1}KP数据的最优解、求解时间和解向量可保存为txt文件或导出 EXCEL文件。
- 扩展功能:再找到最优解后,求出剩余背包容量的大小。
-
D{0-1}KP问题功能设计:该项目由于用到的数据都是其第一步中从文本中读入的数据,只有一个对象。所以其实在该项目中,不需要使用面向对象设计。因为该任务的步骤都是下一步在前面的基础进行操作的,所以面向过程的程序设计更适合该项目。

- 数据读入:
- 由于给的数据集包含很多无用数据,而我们只需要提取其中有效部分的数据。
- 对于有效数据其所在的数据行都是规则的:(以idkp1-10数据集为例)
- 每一组数据都以IDKPX为分界线,且IDKP在数据集中唯一出现,所以读到IDKP这四个字母,就意味着下一行(除空行),包含商品数量与背包容量,再向下数第二行(除空行),是价值,再向下数第二行(除空行),是重量。
- 商品数量与背包容量数据的获取:该行的数字都是有效数据,且商品数量先出现,背包容量数据后出现,这样判断即可得到改行有效数据。
- 对于价格和体积,只要以单个数字为间隔就可以获取有效数据了。
- 流程图:
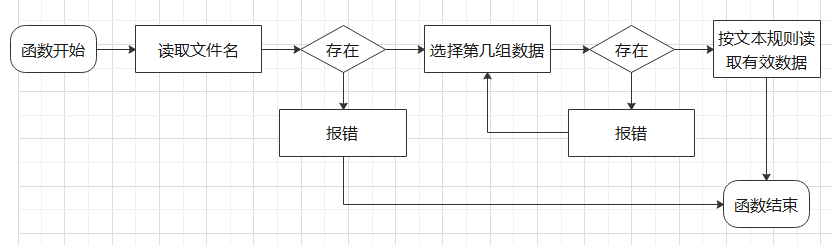
-
数据散点图:
- 开辟一个新的二维数组
data[N][2],其data[N][0]用来存储重量,data[N][1]用来存储价格。同时还需要获取重量和价格的最大值,将其作为散点图的边界。 - 处理完上述数据后,通过调用Java自带的swing库来进行绘制散点图。
- 开辟一个新的二维数组
-
按项集第三项的价值:重量比进行非递增排序:
- 对于数据排序,由于Java中的方法都是值传递,所以在交换数据时Swap方法并不能真正交换原数组的数据。所以我们需要手动交换。
- 关键在于:根据每组打折物品的第三项大小进行排序。交换时,该组物品中的三项都进行交换。
-
自主选择动态规划算法、回溯算法求解指定D{0-1}KP数据的最优解和求解时间:
- 动态规划:由于之前已经介绍过分组背包,在这里直接使用分组背包模板(同时因为数据范围较大,最大数据只需要3000×1e6×4B=12GB的内存空间,所以我们使用数组优化的版本,但这样就无法求出解向量了):
for(int i=1;i<=分组数量;i++) { for(int j=背包总重量;j>=0;j--) { for(int k=1;k<=每组物品个数;k++) { if(weight[i][k]>j) { continue; } if(dp[j]<dp[j-weight[i][k]]+value[i][k]) { dp[j]=dp[j-weight[i][k]]+value[i][k]; //空间优化版本 } if(dp[i][j]<dp[i-1][j-weight[i][k]]+value[i][k]) { dp[i][j]=max(dp[i][j],dp[i-1][j-weight[i][k]]+value[i][k]); //朴素版本 } } } } 不同的问题,其转移方程可能不同。
-
回溯法:
- 由于回溯法的时间复杂度为指数级别,所以数据一大,其就不能在短时间内执行完成了,所以可以设置一个计数变量,每执行一次就+1,当次数大于一个值是,就报错用来提示用户。
- 为了实现简单起见,这里使用递归式调用来进行回溯,其大致框架为:
void dfs(int x){ //更新属性 dfs(x); //恢复现场 }- 回溯法流程图:
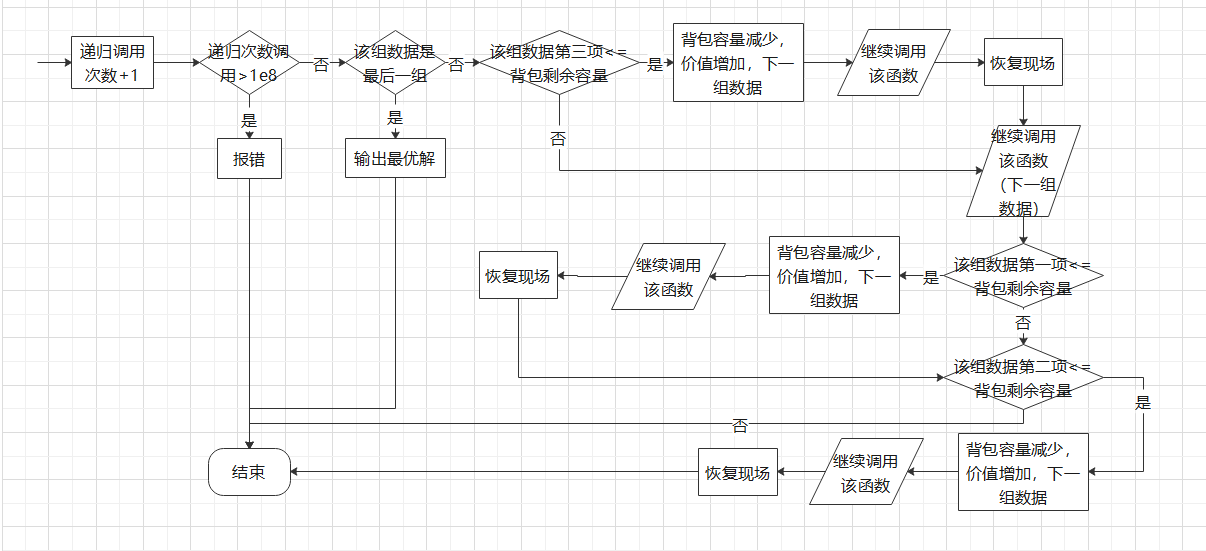
-
保存数据为txt文件或excel文件:
- 输出数据到txt文件,这里使用PrintStream打印输出流实现。
-
扩展功能:得到求出最优解后剩余的背包容量
- 由于动态规划无后效性的性质,在分组背包(D{0-1})问题的
dp[]数组中,其最优解的值在某一段背包容量中是保持不变的,同时该段值不变的数组长度就是其求出最优解后的剩余背包容量。
- 由于动态规划无后效性的性质,在分组背包(D{0-1})问题的
- 数据读入:
-
D{0-1}KP问题功能测试运行:
-
动态规划测试1:
-
运行截图:
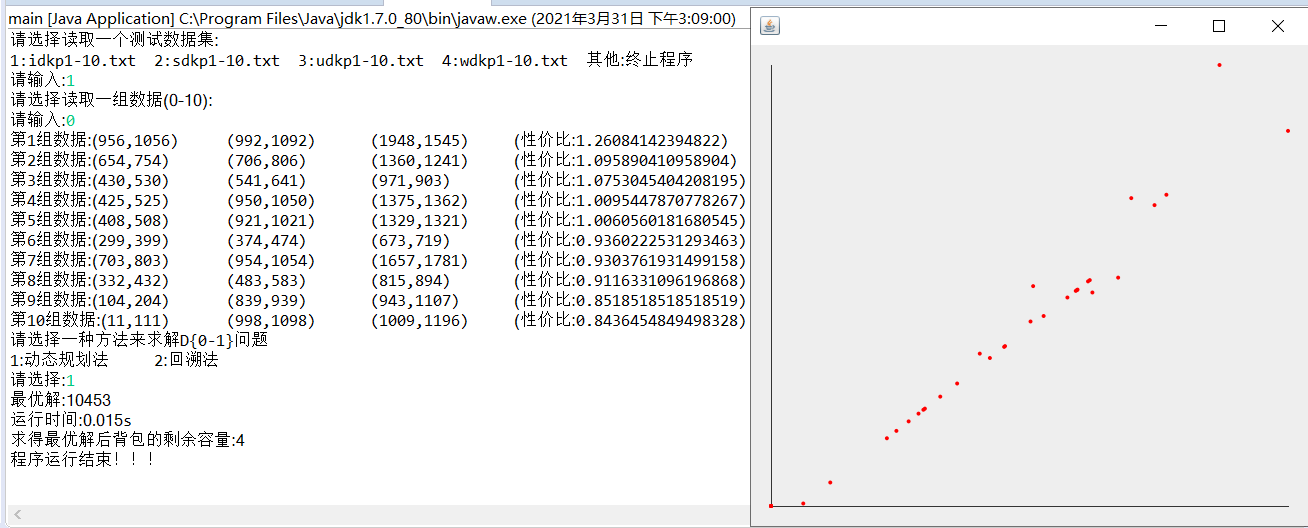
-
结果:

-
-
回溯法测试1:
- 运行截图:
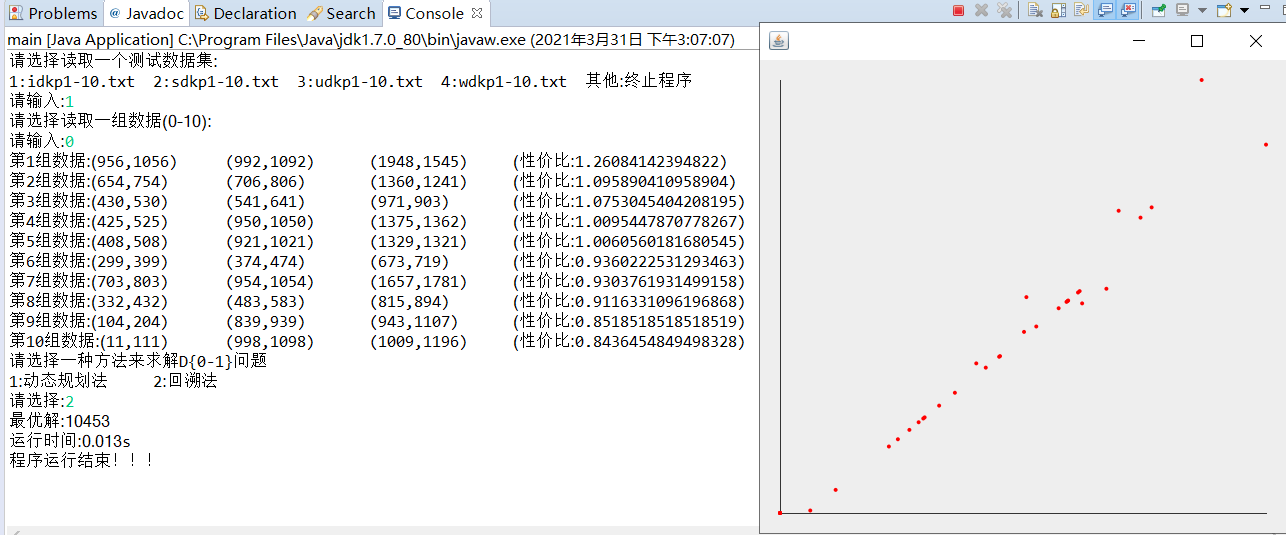
- 运行截图:
-
动态规划测试2(idkp1-10.txt的第10组数据):
- 运行截图:

- 运行截图:
-
回溯法测试2(idkp1-10.txt的第10组数据):
- 运行截图

- 运行截图
-
动态规划测试3(sdkp1-10.txt的第9组数据):
- 运行截图:

- 运行截图:
-
回溯法测试3(sdkp1-10.txt的第9组数据):
- 运行截图:
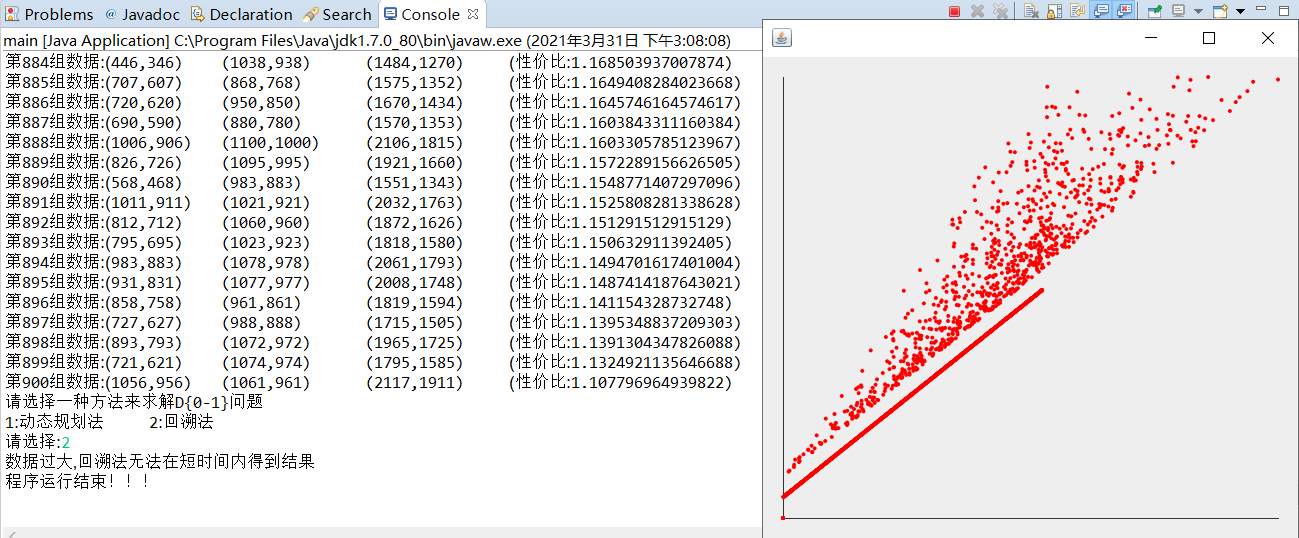
- 运行截图:
-
-
D{0-1}KP问题功能代码片段:
- 数据读入:
//读取背包价值
String profit;
value=new int[10000][5];
int temp_num=0;
profit=in.readLine();
while(profit.isEmpty())
profit=in.readLine();
profit=in.readLine();
while(profit.isEmpty())
profit=in.readLine();
for(i=0;i<profit.length();i++) {
char ch = profit.charAt(i);
if(ch>='0'&&ch<='9') {
temp_num=temp_num*10+ch-'0';
}
else {
value[row][col++]=temp_num;
if(col>3) {
row++;col=1;
}
temp_num=0;
}
}
//读取背包容量
String Weight1;
weight=new int[10000][5];
row=1;col=1;
temp_num=0;
Weight1=in.readLine();
while(Weight1.isEmpty())
Weight1=in.readLine();
Weight1=in.readLine();
while(Weight1.isEmpty())
Weight1=in.readLine();
for(i=0;i<Weight1.length();i++) {
char ch = Weight1.charAt(i);
if(ch>='0'&&ch<='9') {
temp_num=temp_num*10+ch-'0';
}
else {
weight[row][col++]=temp_num;
if(col>3) {
row++;col=1;
}
temp_num=0;
}
}
- 绘制散点图:
protected void paintComponent(Graphics g) {
super.paintComponent(g);
Graphics2D g2 = (Graphics2D)g;
g2.setRenderingHint(RenderingHints.KEY_ANTIALIASING,
RenderingHints.VALUE_ANTIALIAS_ON);
int w = getWidth();
int h = getHeight();
// Draw ordinate.
g2.draw(new Line2D.Double(PAD, PAD, PAD, h-PAD));
// Draw abcissa.
g2.draw(new Line2D.Double(PAD, h-PAD, w-PAD, h-PAD));
double xInc = (double)(w - 2*PAD)/getWeightMax();
double scale = (double)(h - 2*PAD)/getValueMax();
// Mark data points.
g2.setPaint(Color.red);
for(int i = 0; i < data[0].length; i++) {
double x = PAD + xInc*data[0][i];
double y = h - PAD - scale*data[1][i];
g2.fill(new Ellipse2D.Double(x-2, y-2, 4, 4));
}
}
- 动态规划:
public static void DP(){
dp=new int[1000000];
for(int i=1;i<row;i++) {
for(int j=Weight;j>=0;j--) {
for(int k=1;k<=3;k++) {
if(weight[i][k]>j) {
continue;
}
if(dp[j]<dp[j-weight[i][k]]+value[i][k]) {
dp[j]=dp[j-weight[i][k]]+value[i][k];
}
}
}
}
res=dp[Weight];
}
- 回溯法:
public static void dfs(int x){
back_count++;
if(back_count>100000000) {
return;
}
if(x+1>=row) {
return ;
}
else {
if(weight[x+1][3]<=back_weight) {
back_weight-=weight[x+1][3];
back_value+=value[x+1][3];
if(res<back_value) {
res=back_value;
}
dfs(x+1);
back_weight+=weight[x+1][3];
back_value-=value[x+1][3];
}
dfs(x+1);
if(weight[x+1][1]<=back_weight) {
back_weight-=weight[x+1][1];
back_value+=value[x+1][1];
dfs(x+1);
if(res<back_value) {
res=back_value;
}
back_weight+=weight[x+1][1];
back_value-=value[x+1][1];
}
if(weight[x+1][2]<=back_weight) {
back_weight-=weight[x+1][2];
back_value+=value[x+1][2];
if(res<back_value) {
res=back_value;
}
dfs(x+1);
back_weight+=weight[x+1][2];
back_value-=value[x+1][2];
}
}
}
模块化总结:设计该项目时,代码规范的核心为可读性,其实现方法为模块化编程。具体实现为将不同功能分别写在不同的方法之中,同时如果在某一段方法内其中一段代码重复出现,那么就将该代码再次进行封装,写在一个独立的方法里面,要使用时就进行调用。为了方便理解,已将模块化的程序执行用流程图的方式在上面展示出来了。
-
PSP展示:
PSP2.1 任务内容 计划完成需要的时间(min) 实际完成需要的时间(min) Planning 计划 5 10 · Estimate · 估计这个任务需要多少时间,并规划大致工作步骤 5 10 Development 开发 425 560 · Analysis · 需求分析 (包括学习新技术) 5 9 · Design Spec · 生成设计文档 5 6 · Design Review · 设计复审 (和同事审核设计文档) 5 5 · Coding Standard · 代码规范 (为目前的开发制定合适的规范) 10 20 · Design · 具体设计 10 30 · Coding · 具体编码 180(基础功能)+30(重构) 220(基础功能)+60(重构) · Code Review · 代码复审 60 60 · Test · 测试(自我测试,修改代码,提交修改) 120 30(编写过程中得自我测试)+120(成品测试) Reporting 报告 20 50 · Test Report · 测试报告 10 10 · Size Measurement · 计算工作量 5 10 · Postmortem & Process Improvement Plan · 事后总结 ,并提出过程改进计划 5 30 PSP总结:通过本次实验,我们首先通过邹欣老师的《构建之法》一书了解了PSP流程,之后通过在书上学到的方法,在设计与编写个人项目之前进行了PSP流程的设计,其预估总时间为7到8小时,具体在后面有所展示,但最终完成的实际时间远大于预估的时间,其重要误差在于具体设计,具体编码,程序测试与最后的总结等几个环节中。其原因可能是,本人第一次在进行项目开发前对各个流程进行时间上的预估,导致对自己的认识不足,没有考虑在具体设计时会出现的各种突发情况,对各个环节不熟悉等因素。
个人项目总结:对于设计实现D{0-1}背包这个个人项目,我从中也收益良多。首先又一次学习了0-1背包与分组背包这两个经典的背包问题,在之前的学习经验中有了更进一步的任务。学习了Java读取、存储文件,绘制散点图等以前没有学习过的新知识。最后又一次复习了动态规划与回溯法两个经典的算法,以前都是用C/C++来实现的,通过这一次实验,第一次通过Java进行了这两种算法的实现。
不足之处:1.对于解向量,没有很好的方法求出。如果使用动态规划求解,那么其存储数组的某一维空间必须大于等于其背包的容量(这里最大数据约为50万),如果想要解出解向量那么就还需要用一维数组空间来区别物品的组别(最大组数为1000),因为每组有三件物品,那么就至少需要3000*500000的空间来存储数据,空间要求巨大,所以我们必须优化动态规划的空间复杂度(具体方法在背景知识中提出),但当空间缩小为一维时,就无法用常规思路求解向量了。总结如下:对于小数据,可以通过二维数组求解向量,而对于大数据,为了保证空间足够运行,需要进行空间优化,同时也就无法求出解向量了。2.虽然使用了模块化编程,但由于没有使用UI界面,可扩展性较差。
4.任务四:完成任务3的程序开发,将项目源码的完整工程文件提交到你注册Github账号的项目仓库中。
- 使用说明:为了方便检查,本项目仅需要安装jdk1.7及IDE即可下载运行,不需要额外的其他第三方库(但也显得不如使用第三方包的美观)。