算法_约瑟夫问题

有如下游戏：n个人围成一圈，编号为0~n-1，从编号为0的数起，数到编号为m-1者（即数了m个人）剔除，接着从紧接的下一个人从0继续数，以此轮之，最后剩下的那个为胜利者，求其编号。

注：若编号是从1起的，则下面的公式中求模前判断下当值比n大才 mod n 即可。

结果与问题规模n有关：

f(n)=( f(n-1)+m ) mod n，其中f(1)=0。用 c 实现如下：模结果为游戏者的编号，按该递推式求解的时间复杂度为O(n)，代码实现的空间复杂度为O(1)；也可用循环链表模拟该游戏，每次去掉一个节点，复杂度仍为O(n*m)

int f(int n, int m)
{
  int s = 0;
  for (int i = 2; i <= n; i++)
    s = (s + m) % i;
  return s;
}

 

示例：k=2时的结果随n的变化情况（这例子中编号从1起）是个有趣的例子。详可参阅 https://zh.wikipedia.org/wiki/%E7%BA%A6%E7%91%9F%E5%A4%AB%E6%96%AF%E9%97%AE%E9%A2%98

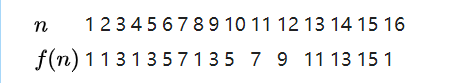
特点：n是2的次幂时，f(n)=1，且为2的次幂的若干个n为界划分为若干个等差数列，该数列是1 3 5 7 9 ...

通解：分解n=2^p+q，其中2^p是不大于n的最大整数，则f(n)=2*q+1。考虑n的二进制形式，容易理解f(n) 是 n的二进制形式的最高位1去掉、剩下部分左移一位、再加1；更简单的理解，把n的二进制形式的最高位1移掉并附加到末尾。

特点的解释：

从该通解可解释上述特点。

对于n为2的次幂时结果为1更直接解释：游戏就是依次剔除2的倍数、3的倍数、4的倍数...的数所以最后剩的只会是1。

2024年央视春晚刘谦的扑克魔术的原理就是上述结论。

 

扩展：

1、若求第k(从0起,k∈[0,n-1])个被剔除者的编号，则用 C 实现如下：时间复杂度为O(lgn)，空间复杂度为O(1)。参考资料：http://maskray.me/blog/2013-08-27-josephus-problem-two-log-n-solutions

int kth(int n, int m, int k)
{
  if (m == 1) return n-1;
  for (k = (k+1)*m-1; k >= n; k = k-n+(k-n)/(m-1));
  return k;
}

 

2、若最开始是从编号为a者数起，则最后剩下的那人的编号与问题规模的关系为：

g(n)=( f(n) +a ) mod n，对该递推式的实现与上类似，空间复杂度为O(n)，时间复杂度为O(1)。

 可用单向循环链表模拟求解每次去掉一个节点，空间复杂度、时间复杂度分别为O(n*m)、O(1)，代码如下：

//n个人，从第k个开始，每次数到m的退出，n、k，m都≥1
typedef struct node
{
    int data;
    struct node* link;
}LNode,*Linklist;
void Josephus(int n,int k,int m)
{
    Linklist list,p,r;
    int i;
    //创建循环链表 
    for(i=1;i<=n;i++)
    {
        p=(Linklist)malloc(sizeof(LNode));
        p->data=i;
        if(i==1)
        {
            list=p;
        }
        else
        {
            r->link=p;
        }
        r=p;
    }//结束后r=p=最后一个节点 
    p->link=list;
    p=list;
    
    //找到第k个
    for(i=1;i<k;i++)
    {
        r=p;
        p=p->link;
    }
    
    //数到m者去除直到只剩一个
    printf("remove: ");
    while(p!=p->link)
    {
        for(i=1;i<m;i++)
        {
            r=p;
            p=p->link; 
        }
        printf("%4d",p->data);
        r->link=p->link;
        free(p);
        p=r->link;
    }
    printf("\nsurvivor:%4d",p->data);
}

 

 

详细推导：http://www.cnblogs.com/qlwy/archive/2012/07/11/2587254.html