分布式系统之数据可靠性（冗余存储中的EC算法）

单机系统或分布式系统中数据可靠性都是通过数据冗余存储来实现的（两者本质上一样），其中多副本方案、纠删码方案是最常见的两种冗余技术（本质上前者是后者的特例）。

本文通俗易懂地介绍纠删码的原理（Erasure-Code，EC算法）、实现。详见文章 “EC算法、EC实现、EC优化”。

关键词：数据可靠性、冗余、多副本、RAID、EC算法

 

以下为阅毕的总结以备忘

=======================

数据可靠性

分布式系统中，数据存储的可靠性（数据整体上看没有丢失或损坏，但允许局部丢失或损坏）是分布式系统的第一个问题，若数据不可靠则讨论分布式系统的可用性、性能、数据一致性等都没什么意义了。

冗余存储

然而磁盘上部分数据的丢失或损坏是不可避免的，特别是在大数据场景下问题更突出。不管在单机系统还是分布式系统下，要做到数据整体上不丢失或损坏，最直接简单的方法就是对一份数据冗余存储副本。具体而言，单机系统下是RAID技术、分布式系统下是EC（Erasure-Code，擦出吗，纠删码）技术。

RAID：容错式磁盘阵列（RAID, Redundant Array of Independent Disks），简称磁盘阵列

RAID 本质上跟EC没有区别, 它是单机系统时代被广泛使用的成熟实现。EC可以认为是分布式系统发展起来后, RAID算法在多机系统上的重新实现：

• • RAID-0 相当于无冗余;
  • RAID-1 相当于1冗余;
  • RAID-5 相当于EC的k+1模式, k个数据块+1个校验块;
  • RAID-6 相当于EC的k+2模式, k个数据块+2个校验块，且k=10；

冗余存储方案

若在最多允许m个数据丢失或损坏的情况下做到数据整体上仍可靠，该怎么做？（在实际分布式系统中，m通常取3）

• 多副本：简单的做法是每个数据都多存m个副本即可，例如Kafka内部数据的replication就是这种。其优点是简单、缺点是冗余率太高了，为 m/(1+m)。此方案可认为是下述方案的特例。
• 纠删码：EC算法的做法则是针对k个原始数据算出m个冗余数据，将k+m个数据一起存储，这样冗余率大大降低，为 m/(k+m)。其k+m个数据中任意最多m个丢失也能恢复。可见，上述方案就是这里当k=1时的情形！！

EC算法原理

定义 y = d₁ + d₂x + d₃x² + ... d_kx^k-1，其中 i∈[1,k]的d_i 表示个原始数据，d_i为自变量。

编码——如何计算冗余数据（称为校验块数据）：x 任取 m个值得到的m个y即为冗余数据，为计算方便，取x∈[1,m]，得到k+m个数据 d₁、d₂、...、d_k、y₁、...、y_m 。实际上，它们构成了自变量为d_i的包含m个方程的k元一次方程组，x的取值构成了方程组的系数矩阵：

该m*k的系数矩阵就是著名的 Vandermonde 矩阵。它只是 EC 算法中的1种系数选择方式，其他常用的系数矩阵还有 Cauchy 矩阵等。

该矩阵保证了任意n*n的子矩阵都是线性无关的, 构成的方程肯定有唯一解。

解码——如何恢复丢失数据：假设 k+m 个数据中丢失了q个（其中q≤m）数据，则从上述方程组中随意取q个方程组成q元一次方程组，求解即可得到丢失数据。

实现

可见，EC算法原理上并不复杂，背后是简单的数学。不过，这套理论还不能直接应用到线上产品中，因为计算机中还要考虑数字大小限制，例如k个32位整数作为数据，通过Vandermonde矩阵生成校验块, 那校验块的数值几乎确定会溢出。因此在实现上会借助伽罗华域上的四则运算来替代普通的四则运算以加快计算。详情可参阅EC算法的实现。

可靠性分析（见这篇文章）：

 

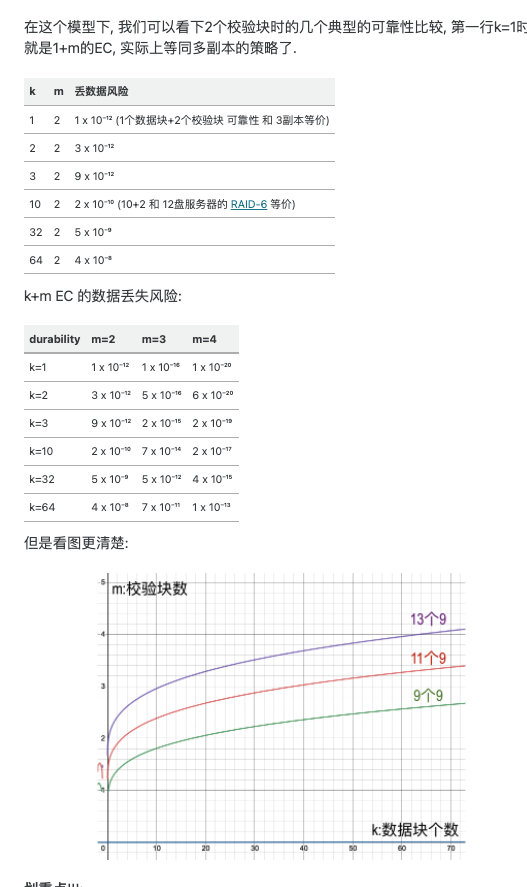
可见，k一定时m越大越可靠、m一定时k越大越不可靠，符合直觉。

值得注意的是，取k=1, m=2时, 相当于一个数据三份存储，大约可以达到11~12个9。这也是aws-s3承诺的11个9的由来（s3-durability）。 

PS：这里涉及数据可靠性度量的“x个9”的说法，系统可用性的度量中同样有此说法。后者是 MTTF/( MTTF + MTTR ) 的值，其中MTTF、MTTR分别表示系统的连续运行平均时长、故障解决的平均时长。

 

 

小感悟：把一个本来看上去很工程的问题抽象成了数学问题，从而从理论上进行了清晰、详尽、透彻、漂亮的表示、分析、解决，美哉！！！