HMM_概率计算——forwar_algorithm实现
一、前向算法（递推）
1）观测概率初值：
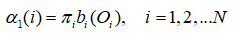
2）递推：
3）终止：
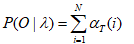
二、理解前向算法
哈哈，先欠着，没时间码字！
三、代码实现：
1 def getPro(): 2 iniStatePro=[] #初始状态概率分布列表 3 pi=np.array(iniStatePro) 4 5 stateTransPro=[] #状态转移概率矩阵 N x N 6 A=np.array(stateTransPro) # A[a][b]： 状态a -> 状态b 的概率 7 8 observationPro=[] #观测概率矩阵 N x M 9 B=np.array(observationPro) # B[a][o]：状态a->观测值o的概率 10 return A,B,pi; 11 12 def getForwardPro(A,B,pi,T,O): #O为观测序列 13 alpha=np.zeros(shape=(T,len(A))) #定义前向概率 14 for i in range(len(B)): #初始化前向概率分布 15 alpha[0][i]=pi[i]*B[ i ][ O[0] ] 16 17 for t in range(1,T): # 递推 18 for i in range( len(A) ): # t时刻每个状态 19 pro=0 20 for j in range( len(B) ): # 前一状态到当前时刻 联合概率 21 pro=pro+ A[j][i]*alpha[t-1][j]; 22 alpha[t][i]=pro*B[i][ O[t] ] #预测概率 23 OSeqBaseLambdaPro=sum( alpha[T-1] ); # p( O| lambda ) 24 return OSeqBaseLambdaPro;
四、验证：统计学习方法 177 编程实现
1 def getPro(): 2 iniStatePro=[ 0.2 ,0.4, 0.4 ] #初始状态概率分布列表 3个状态 3 pi=np.array(iniStatePro) 4 5 stateTransPro=[[ 0.5,0.2,0.3 ],[ 0.3,0.5,0.2 ],[ 0.2, 0.3, 0.5 ]] #状态转移概率矩阵 N x N 6 A=np.array(stateTransPro) # A[a][b]： 状态a -> 状态b 的概率 7 8 observationPro=[[0.5,0.5],[0.4,0.6],[0.7,0.3]] #观测概率矩阵 N x M [红，白] 9 B=np.array(observationPro) # B[a][o]：状态a->观测值o的概率 10 11 return A,B,pi; 12 13 def getForwardPro(A,B,pi,T,O): #O为观测序列 14 alpha=np.zeros(shape=(T,len(A))) #定义前向概率 15 for i in range(len(B)): #初始化前向概率分布 16 alpha[0][i]=pi[i]*B[ i ][ O[0] ] 17 18 for t in range(1,T): # 递推 19 for i in range( len(A) ): # t时刻每个状态 20 pro=0 21 for j in range( len(B) ): # 前一状态到当前时刻 联合概率 22 pro=pro+ A[j][i]*alpha[t-1][j]; 23 alpha[t][i]=pro*B[i][ O[t] ] #预测概率 24 OSeqBaseLambdaPro=sum( alpha[T-1] ); # p( O| lambda ) 25 return OSeqBaseLambdaPro; 26 27 A,B,pi=getPro(); 28 T=3 29 O=[0,1,0] 30 pro=getForwardPro(A,B,pi,T,O) 31 print(pro)
结果：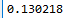
书上答案：0.13022
