数学——广义Lagrange
一、多元函数条件极值(高数同济第七版 P116 有相关章节)
1、转换为求解非条件极值
例题:用钢板做一个体积为2的长方形水箱。问 长宽高各取怎样的尺寸 用料最省?
设该长方形冰箱的长宽高非别为为x,y,z 。 即:
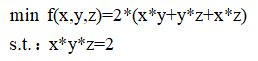
我们可以将其转换为求解非条件极值,然后分别求偏导后求解:
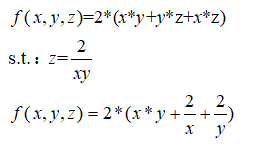
2、 拉格朗日数乘求解
a)了解拉格朗日数乘:将最优问题化转化为一个方程组,进行求解。
 求解 f(x,y)在约束条件下的最小值!
求解 f(x,y)在约束条件下的最小值!
i) 由隐函数存在定理可知:
ii) 假设在 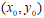 处取极值,则
处取极值,则

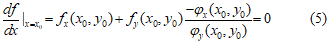
iii) 令
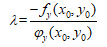 ,称λ为lagrange乘子
,称λ为lagrange乘子
得: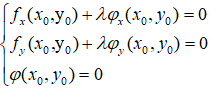 ,其中三个方程,三个未知数,直接可以解方程。
,其中三个方程,三个未知数,直接可以解方程。
b)总结:我们引入辅助函数: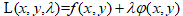 ,称
,称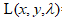 为Lagrange函数
为Lagrange函数
即: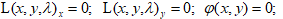
以上还可以推广:
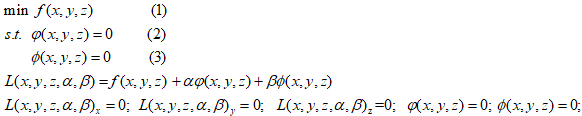
二、Lagrange对偶性、广义Larange函数:
在一般的优化模型中,约束条件不但有等式约束也有不等式约束,第一部分中只有等式约束,针对这一问题,我们可以通过广义lagrange函数解决:
结论:

证明:语言理解
假设:我们给定一个x,若其中有一个 或
或  ,则存在
,则存在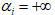 或
或  使得
使得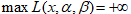
若给定的x不会破坏约束条件,则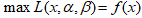
即:

在不破坏约束条件的情况下:
综述:
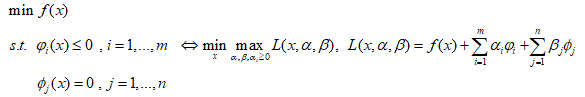
三、支持向量机 ——最大间隔分离超平面
1、最优模型转换
最大间隔分离超平面一句话:使距离超平面最近的点的距离极大化

求解:
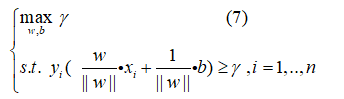
首先我们对模型(7)进行处理,给定一个 i 使得  最小,由于 w,b 成比例放大缩小,该超平面还是原来的超平面,
最小,由于 w,b 成比例放大缩小,该超平面还是原来的超平面,
且不影响目标函数,不影响约束条件。因此给定一个λ 使得 ,即
,即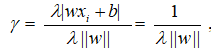
那么得到优化模型(7)的新模型(8)
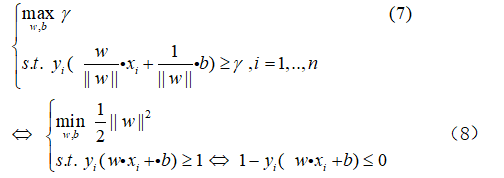



 浙公网安备 33010602011771号
浙公网安备 33010602011771号