机器学习中的一些概念知识
点三个横,打开目录浏览
1、激活函数 (参看)
Layer保存自己认为重要的特征,每一层都是sampling,激活函数的本初就是分类,把数据投影到例如[0,1]区间内
神经网络模型如下图,把一大堆的输入累加起来,然后给一个输出,但是这还不够,因为这样还是线性的:加系数+加权重,还是线性,线性意味着神经网络没法你和非线性函数,
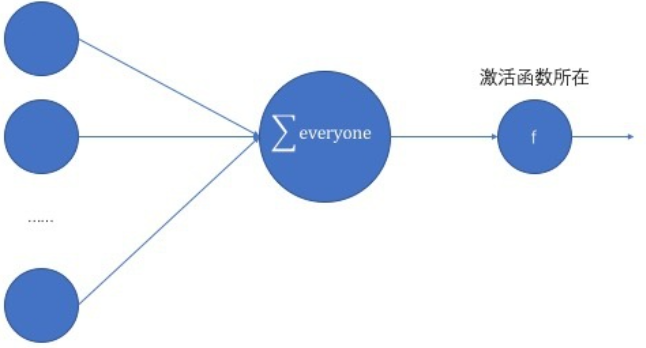
那我们搞一个非线性的变化,让输出变一变,于是引入了激活函数,从历史看,大家显示发现了sigmoid,tanh这类的函数,好处就是求导方便(为啥求导呢,因为神经网络需要反向传播)
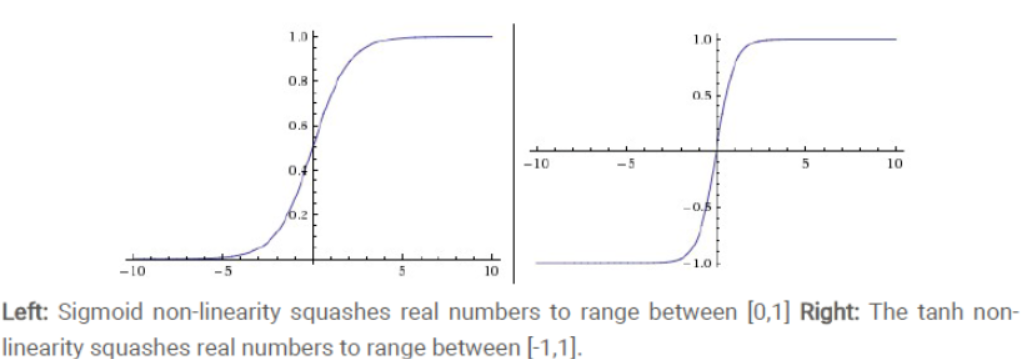
1.1 sigmod函数
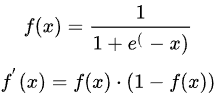
sigmod函数,在远离0点的地方,梯度变得非常微小,所以求导以后也很难知道我们的反向传播该怎样梯度下降。所以,你需要尤其注意参数的初始值来尽量避免saturation的情况。如果你的初始值很大的话,大部分神经元可能都会处在saturation的状态而把gradient kill掉,这会导致网络变的很难学习。
Sigmoid 的 output 不是0均值. 这是不可取的,因为这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。
产生的一个结果就是:如果数据进入神经元的时候是正的(e.g. elementwise in ),那么 计算出的梯度也会始终都是正的
1.2 tanh函数
tanh(x)的梯度消失问题比sigmoid要轻.梯度如果过早消失,收敛速度较慢.
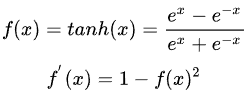
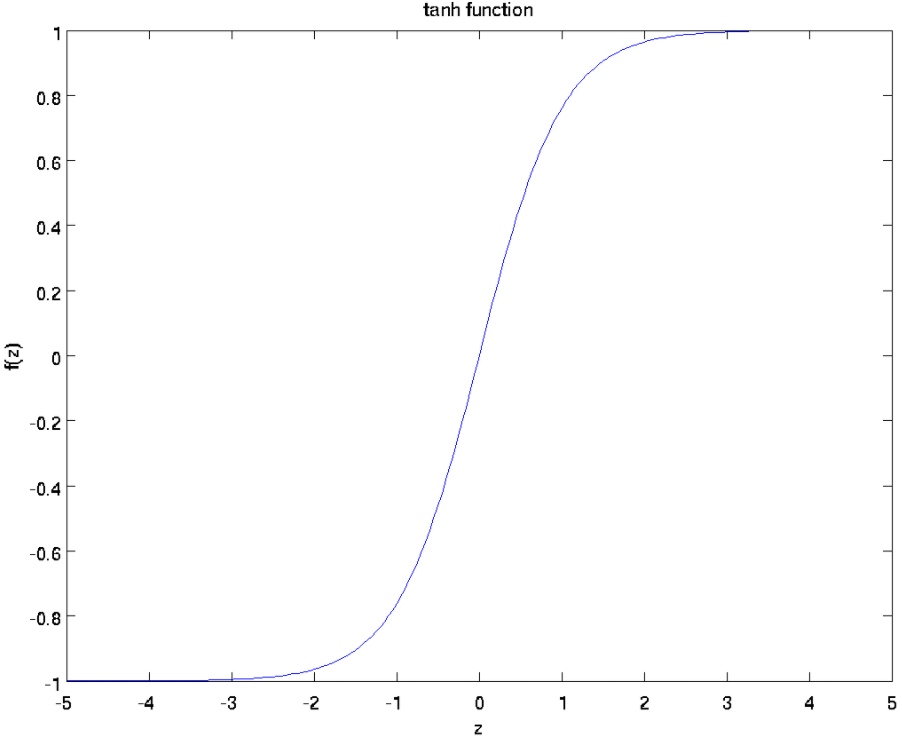
(1)输入较大或者较小时,输出几乎是平滑的并且梯度较小,这不利于权重更新。与sigmod相比在于输出间隔,tanh的输出间隔为1,并且整个函数以0为中心,比sigmod好
(2)在tanh图中,负输入将被强映射为负,而零输入被映射为接近为0
1.3 ReLU函数
于是计算精度就得高,计算就会变慢,然后出现了下面这个:
![]()
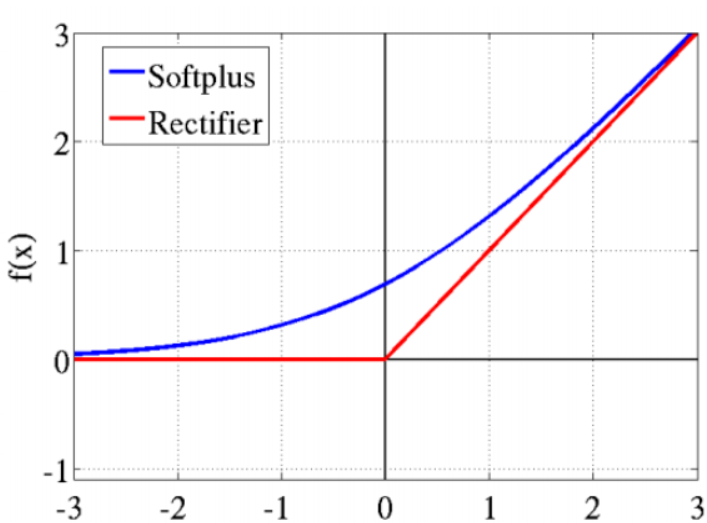
这个模型对比Sigmoid系主要变化有三点:①单侧抑制 ②相对宽阔的兴奋边界 ③稀疏激活性(重点,可以看到红框里前端状态完全没有激活)
这是一个很像分段函数的函数,它求导很快,但是也存在这个两个问题:(1)0点附近不可微,所以通常在0点只求右导数;(2)它会“谋杀”一些神经元,既是说它在返乡传播过程中很快让一些神经元的导数永远为0,于是这些神经元等于被抛弃了,也就是被“谋杀”了,这当然提高了训练速断,不过也武断了些,为了解决这个问题,我们引入了:
![]()
也就是说,不让ReLU武断的将一些<0的数归结为0,而是给一个很小的系数,让他们稍微偏离一点0,就好像漏了一样,称为leaky。
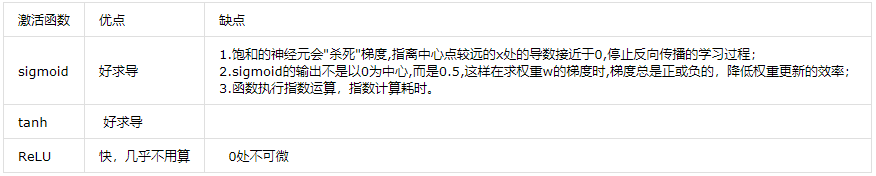
1.4 激活函数总结
1.5 softmax
ReLU通常只能用在隐含层的,输出层不用的,例如二分类就是sigmod,多分类就是softmax。
在一般的二分类问题中,tanh用于隐藏层,sigmod用户输出层。
- 从计算的角度,Sigmoid 和 tanh 激活函数均需要计算指数,复杂度高,而Relu 只需要一个阈值就可得到激活值。
- Relu 的非饱和性可以有效的解决梯度消失问题,提供相对宽的激活边界
- Relu 的单侧抑制提供了网络的稀疏表达能力
3、自然界中的一些分布
数学前辈们,探寻出一些概率分布,我们现在对数据进行处理,看看符合那种自然分布,以分布函数来预测等会更为准确
4、似然、贝叶斯
p(x|θ) 似然求解θ;
p(θ|x) 贝叶斯求解x,具体可以看看https://www.cnblogs.com/z-712/p/14817763.html
5、正则化
范数,L1范数,L2范数 范数都是距离计算的一种,如下,具体可以参考《数值分析》

左面是L2(x^2+y^2)约束下解空间的图像,右面是L1(|x|+|y|)约束下解空间的图像。
蓝色的圆圈表示损失函数的等值线。同一个圆上的损失函数值相等的,圆的半径越大表示损失值越大,由外到内,损失函数值越来越小,中间最小。
如果没有L1和L2正则化约束的话,w1和w2是可以任意取值的,损失函数可以优化到中心的最小值的,此时中心对应的w1和w2的取值就是模型最终求得的参数。
但是填了L1和L2正则化约束就把解空间约束在了黄色的平面内。黄色图像的边缘与损失函数等值线的交点,便是满足约束条件的损失函数最小化的模型的参数的解。 由于L1正则化约束的解空间是一个菱形,所以等值线与菱形端点相交的概率比与线的中间相交的概率要大很多,端点在坐标轴上,一些参数的取值便为0。L2正则化约束的解空间是圆形,所以等值线与圆的任何部分相交的概率都是一样的,所以也就不会产生稀疏的参数。详见https://zhuanlan.zhihu.com/p/164560266
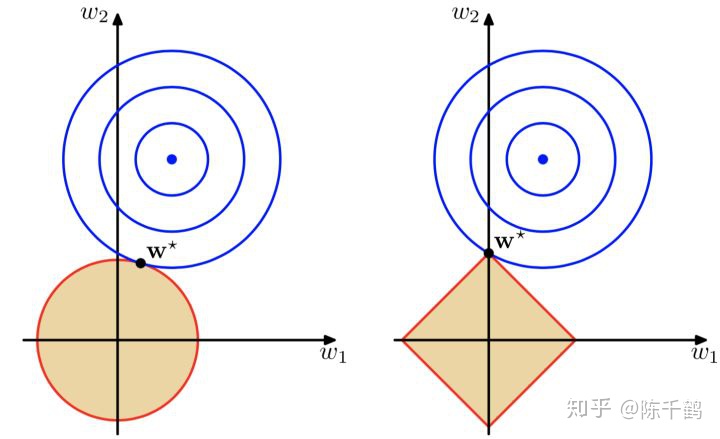
总而言之,范数作用于权重矩阵等,防止过拟合,过于多的参数,是可以达到很好的效果,但是容易过拟合,正则化就是来约束参数数量,防止过拟合,但又可以保证曲线的光滑程度,具体还可以看一下这篇
梯度是一种矢量,对应到数学里就是偏导数,一些训练次数和层数太多时,也即是求导次数次增多,导数趋近于0,导致梯度消失
一些优化算法,对偏导前面即分母上,系数进行变换(一般默认为1),如Adam优化,弹性放缩系数
6、Batch size
Batch_size 是用于在每次迭代中训练模型的数据数量,一般的设置是32、64、128、256、512
选择正确的Batch_size用于确保cost function和参数值的收敛,以及模型的泛华能力
Batch_size决定更新的频率,Batch_size越小,更新就越快
Batch越大,梯度越精准,也就是说,在迭代计算的时候更容易跳过局部区域
比较打的Batch_size,往往GPU memory是不够用的,需要通过并行计算的方式解决[1]
7、有监督/无监督 学习中的 训练集和测试集
有监督学习中:https://blog.csdn.net/zzj_csdn/article/details/103228738/
无监督学习中:https://zhuanlan.zhihu.com/p/32387092
节选 1 参数
有了模型后,训练集就是用来训练参数的,说准确点,一般是用来梯度下降的。而验证集基本是在每个epoch完成后,用来测试一下当前模型的准确率。因为验证集跟训练集没有交集,因此这个准确率是可靠的。那么为啥还需要一个测试集呢?
这就需要区分一下模型的各种参数了。事实上,对于一个模型来说,其参数可以分为普通参数和超参数。在不引入强化学习的前提下,那么普通参数就是可以被梯度下降所更新的,也就是训练集所更新的参数。另外,还有超参数的概念,比如网络层数、网络节点数、迭代次数、学习率等等,这些参数不在梯度下降的更新范围内。尽管现在已经有一些算法可以用来搜索模型的超参数,但多数情况下我们还是自己人工根据验证集来调
那也就是说,从狭义来讲,验证集没有参与梯度下降的过程,也就是说是没有经过训练的;但从广义上来看,验证集却参与了一个“人工调参”的过程,我们根据验证集的结果调节了迭代数、调节了学习率等等,使得结果在验证集上最优。因此,我们也可以认为,验证集也参与了训练。
那么就很明显了,我们还需要一个完全没有经过训练的集合,那就是测试集,我们既不用测试集梯度下降,也不用它来控制超参数,只是在模型最终训练完成后,用来测试一下最后准确率
聪明的读者就会类比到,其实这是一个无休止的过程。如果测试集准确率很差,那么我们还是会去调整模型的各种参数,这时候又可以认为测试集也参与训练了。好吧,我们可能还需要一个“测试测试集”,也许还需要“测试测试测试集”...
算了吧,还是在测试集就停止吧。
对于有监督学习,由于标签作为输入端,其作用于训练集(Test set)和验证集(Validation set)上;对于无监督习,标签主要作用于验证集(Validation set)上。
标签对无监督算法有什么用呢?
1. 标签用来评价无监督学习,也就是来判断无监督学习的好坏。其常用指标有三个:检测率(Detection rate),召回率(Recall)和准确率(precision)。你的模型到底好不好?来,跟我们现在的标签比对一下,看你和我的交集(overlap)有多少,看你比我多抓了多少坏人!
2. 标签用来调优无监督模型,也就是标签作用于验证集上。任何一种机器学习算法都包含参数,调参是模型调优的主要工作。有监督的调参主要在training set上进行,例如ANN的权值;而无监督没有training set,调参主要是在validation set上进行。换言之,有监督的标签是用来输入训练模型的,无监督的标签是研究人员用来看(验证)的。
8、梯度下降
梯度下降算法步骤:
(1)初始化随机权重和偏差
(2)把输入传入网络,得到输出值
(3)计算真实值和预测值(输出值)之间的误差
(4)对每一个产生误差的神经元,改变相应的(权重)值减小误差
(5)迭代更新,直到找到最佳权重
参考链接
[1] https://blog.csdn.net/weixin_38477351/article/details/108965622


 浙公网安备 33010602011771号
浙公网安备 33010602011771号