CCF201812-Python题解
原题连接: http://118.190.20.162/view.page?gpid=T80
试题编号: 201812-1
试题名称: 小明上学
时间限制: 1.0s
内存限制: 512.0MB
题目背景
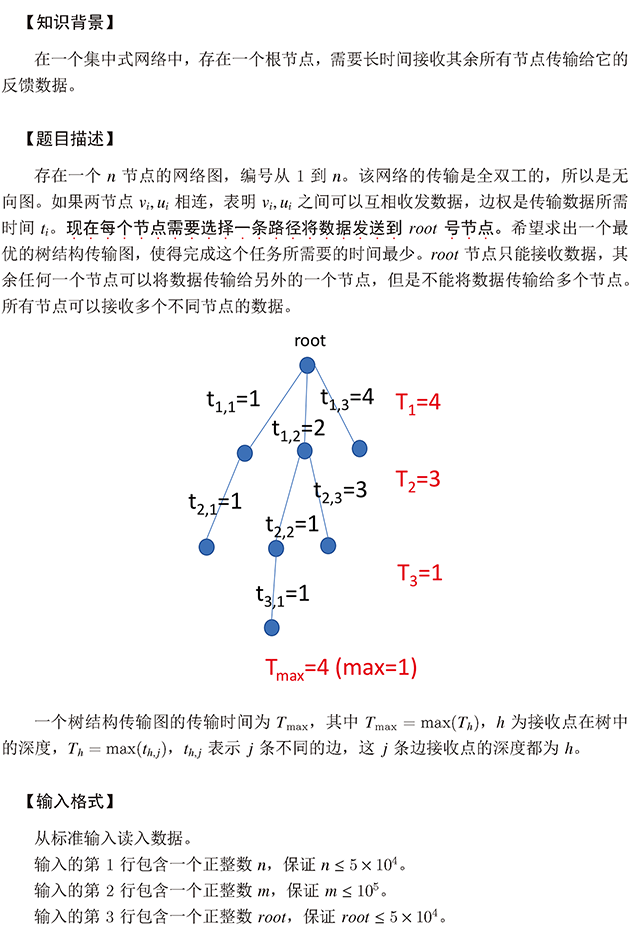
小明是汉东省政法大学附属中学的一名学生,他每天都要骑自行车往返于家和学校。为了能尽可能充足地睡眠,他希望能够预计自己上学所需要的时间。他上学需要经过数段道路,相邻两段道路之间设有至多一盏红绿灯。
京州市的红绿灯是这样工作的:每盏红绿灯有红、黄、绿三盏灯和一个能够显示倒计时的显示牌。假设红绿灯被设定为红灯 r 秒,黄灯 y 秒,绿灯 g 秒,那么从 0 时刻起,[0,r) 秒内亮红灯,车辆不许通过;[r, r+g) 秒内亮绿灯,车辆允许通过;[r+g, r+g+y) 秒内亮黄灯,车辆不许通过,然后依次循环。倒计时的显示牌上显示的数字 l(l > 0)是指距离下一次信号灯变化的秒数。
问题描述
一次上学的路上,小明记录下了经过每段路的时间,和各个红绿灯在小明到达路口时的颜色和倒计时秒数。希望你帮忙计算此次小明上学所用的时间。
输入格式
输入的第一行包含空格分隔的三个正整数 r、y、g,表示红绿灯的设置。这三个数均不超过 106。
输入的第二行包含一个正整数 n(n ≤ 100),表示小明总共经过的道路段数和看到的红绿灯数目。
接下来的 n 行,每行包含空格分隔的两个整数 k、t。k=0 表示经过了一段道路,耗时 t 秒,此处 t 不超过 106;k=1、2、3 时,分别表示看到了一个红灯、黄灯、绿灯,且倒计时显示牌上显示的数字是 t,此处 t 分别不会超过 r、y、g。
输出格式
输出一个数字,表示此次小明上学所用的时间。
样例输入
30 3 30
8
0 10
1 5
0 11
2 2
0 6
0 3
3 10
0 3
样例输出
70
样例说明
小明先经过第一段道路,用时 10 秒,然后等待 5 秒的红灯,再经过第二段道路,用时 11 秒,然后等待 2 秒的黄灯和 30 秒的红灯,再经过第三段、第四段道路,分别用时6、3秒,然后通过绿灯,再经过最后一段道路,用时 3 秒。共计 10 + 5 + 11 + 2 + 30 + 6 + 3 + 3=70 秒。
评测用例规模与约定
测试点 1, 2 中不存在任何信号灯。
测试点 3, 4 中所有的信号灯在被观察时均为绿灯。
测试点 5, 6 中所有的信号灯在被观察时均为红灯。
测试点 7, 8 中所有的信号灯在被观察时均为黄灯。
测试点 9, 10 中将出现各种可能的情况。
题解
模拟叭,少年 rgy
rr, yr, gr = input().split()
r, y, g = int(rr), int(yr), int(gr)
n = int(input())
time = 0
for _ in range(n):
kr, tr = input().split()
k, t = int(kr), int(tr)
if k == 0:
time = time + t
elif k == 1:
time = time + t
elif k == 2:
time = time + t + r
elif k == 3:
pass
print(time)
原题连接: http://118.190.20.162/view.page?gpid=T81
试题编号: 201812-2
试题名称: 小明上学
时间限制: 1.0s
内存限制: 512.0MB
问题描述:
题目背景
汉东省政法大学附属中学所在的光明区最近实施了名为“智慧光明”的智慧城市项目。具体到交通领域,通过“智慧光明”终端,可以看到光明区所有红绿灯此时此刻的状态。小明的学校也安装了“智慧光明”终端,小明想利用这个终端给出的信息,估算自己放学回到家的时间。
问题描述
一次放学的时候,小明已经规划好了自己回家的路线,并且能够预测经过各个路段的时间。同时,小明通过学校里安装的“智慧光明”终端,看到了出发时刻路上经过的所有红绿灯的指示状态。请帮忙计算小明此次回家所需要的时间。
输入格式
输入的第一行包含空格分隔的三个正整数 r、y、g,表示红绿灯的设置。这三个数均不超过 106。
输入的第二行包含一个正整数 n,表示小明总共经过的道路段数和路过的红绿灯数目。
接下来的 n 行,每行包含空格分隔的两个整数 k、t。k=0 表示经过了一段道路,将会耗时 t 秒,此处 t 不超过 106;k=1、2、3 时,分别表示出发时刻,此处的红绿灯状态是红灯、黄灯、绿灯,且倒计时显示牌上显示的数字是 t,此处 t 分别不会超过 r、y、g。
输出格式
输出一个数字,表示此次小明放学回家所用的时间。
样例输入
30 3 30
8
0 10
1 5
0 11
2 2
0 6
0 3
3 10
0 3
样例输出
46
样例说明
小明先经过第一段路,用时 10 秒。第一盏红绿灯出发时是红灯,还剩 5 秒;小明到达路口时,这个红绿灯已经变为绿灯,不用等待直接通过。接下来经过第二段路,用时 11 秒。第二盏红绿灯出发时是黄灯,还剩两秒;小明到达路口时,这个红绿灯已经变为红灯,还剩 11 秒。接下来经过第三、第四段路,用时 9 秒。第三盏红绿灯出发时是绿灯,还剩 10 秒;小明到达路口时,这个红绿灯已经变为红灯,还剩两秒。接下来经过最后一段路,用时 3 秒。共计 10+11+11+9+2+3 = 46 秒。
评测用例规模与约定
有些测试点具有特殊的性质:
* 前 2 个测试点中不存在任何信号灯。
测试点的输入数据规模:
* 前 6 个测试点保证 n ≤ 103。
* 所有测试点保证 n ≤ 105。
题解
和第一题比,要有一个update_time,这里主要以下时间的判断
r,y,g=map(int,input().split())
n=int(input())
def update(past_time,k,t):
if k==0:
return t
elif k==1: #r
if past_time>t: # 到现在为止已经过去了多长时间,现在的信号时什么,需要等待多久
return update(past_time-t,3,g)
else:
return t-past_time
elif k==2:#y
if past_time>t:
return update(past_time-t,1,r)
else:
return t-past_time+r
elif k==3:#g
if past_time>t:
return update(past_time-t,2,y)
else:
return 0
time=0
for _ in range(n):
k,t=map(int, input().split())
time+=update(time%(r+g+y),k,t)
print(time)
试题编号: 201812-3
试题名称: CIDR合并
时间限制: 1.0s
内存限制: 512.0MB



样例输入
2
1
2
样例输出
1.0.0.0/8
2.0.0.0/8
样例输入
2
10/9
10.128/9
样例输出
10.0.0.0/8
样例输入
2
0/1
128/1
样例输出
0.0.0.0/0


题解
目前简单排序,复杂的不想写

n=int(input())
def format_ip(ip):
if '/' in ip:
dots=ip.count('.')
if dots==3:
ip=ip
else:#省略后缀型
pre,lens=ip.split('/')
if dots==0:
ip=pre+'.0.0.0/'+lens
elif dots==1:
ip=pre+'.0.0/'+lens
elif dots==2:
ip=pre+'.0/'+lens
else:#省略长度型
dots=ip.count('.')
if dots==0:
ip+='.0.0.0/8'
elif dots==1:
ip+='.0.0/16'
elif dots==2:
ip+='.0/24'
elif dots==3:
ip+='/32'
return ip
def count_value(ip):
tmp=ip.split('.')
v=0
for i in range(4):
v+=int(tmp[i])*256**(3-i)
return v
ip_list=[]
for _ in range(n):
ip=input()
ip=format_ip(ip)
pre_ip,lens=ip.split('/')
value=count_value(pre_ip)
lens=int(lens)
ip_list.append([ip,value,lens])
res=sorted(ip_list, key=lambda u:[u[1],u[2]])
for i in res:
print(i[0])
试题编号: 201812-4
试题名称: 数据中心
时间限制: 1.0s
内存限制: 512.0MB

样例输入
4
5
1
1 2 3
1 3 4
1 4 5
2 3 8
3 4 2
样例输出
4
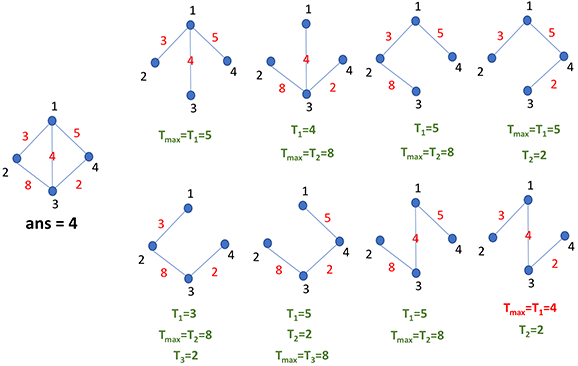
样例说明
下图是样例说明。
题解
并查集+Kruskal,最小生成树最短边
def find(forest, item):
if forest[item]!=item:
forest[item]=find(forest,forest[item])
return forest[item]
def Kruskal(nodes, edges):
forest={}
for node in nodes:
forest[node]=node
MST=[]
edges=sorted(edges,key=lambda u:u[2])
num=len(nodes)-1
for e in edges:
t1,t2,_=e
parent1=find(forest,t1)
parent2=find(forest,t2)
if parent1!=parent2:
MST.append(e)
num-=1
if num==0:
# print(forest)
return MST
else:
forest[parent2]=parent1
if __name__=="__main__":
n=int(input())
m=int(input())
root=int(input())
nodes=list(range(1, n+1))
edges=[]
for _ in range(m):
edges.append(list(map(int, input().split())))
mst=Kruskal(nodes, edges)
res=0
for ms in mst:
if ms[-1]>res:
res=ms[-1]
print(res)




