p3412 [POI2005]SKO-Knights

传送门

分析

图1

我们假设我们现在有两个向量(2,3)和(4,2)，将他们所能到达的点在几何画板上画出来，再将这些点用红线连起来，在将横坐标相同的点用蓝线连起来便能得到图1，就此我们可以发现可以用绿色的两个向量取代之前的两个向量，并且发现有一个向量可以是(0,B)的形式。在发现这个之后我们现在的任务便是求出新向量和原向量的关系了，见下边的推导：

      

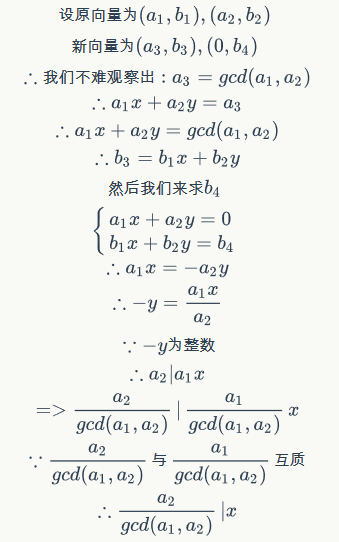
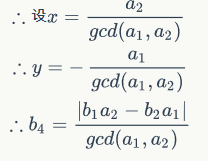
所以我们可以将任何两个向量转变成一个在y轴的向量和一个其它向量。所以我们只需要不断的将向量转变到y轴上使得最终至多一个向量不再y轴上就行了。注意在y轴上的向量我们可以通过取它们的gcd将它们合并成一个向量。详见代码。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cctype>
#include<cmath>
#include<cstdlib>
#include<queue>
#include<ctime>
#include<vector>
#include<set>
#include<map>
#include<stack>
using namespace std;
int a[500],b[500];
inline void exgcd(int a,int b,int &x,int &y){
      if(b==0){
          x=1;
          y=0;
          return;
      }
      exgcd(b,a%b,x,y);
      int z=x;
      x=y;
      y=z-(a/b)*y;
      return;
}
int main(){
      int n,m,i,j,k,x,y;
      scanf("%d",&n);
      for(i=1;i<=n;i++){
          scanf("%d%d",&a[i],&b[i]);
      }
      int a1,b1,a2,b2;
      if(!a[1]){
          a1=a[2];
          b1=b[2];
          b2=b[1];
      }else if(!a[2]){
          a1=a[1];
          b1=b[1];
          b2=b[2];
      }else {
        a1=__gcd(a[1],a[2]);
        exgcd(a[1]/a1,a[2]/a1,x,y);
        b1=b[1]*x+b[2]*y;
        b2=abs(b[1]*a[2]-b[2]*a[1])/a1;
      }
      for(i=3;i<=n;i++){
          if(!a1){
            a1=a[i];
            b2=__gcd(b2,b1);
            b1=b[i];
        }else if(!a[i]){
            b2=__gcd(b2,b[i]);
        }else {
            int be=a1,be2=b1;
            a1=__gcd(a1,a[i]);
          exgcd(be/a1,a[i]/a1,x,y);
          b1=b1*x+b[i]*y; 
          b2=__gcd(b2,abs(be2*a[i]-b[i]*be)/a1);
        }
      }
      cout<<a1<<' '<<b1<<endl<<0<<' '<<b2<<endl;
      return 0;
}