100211D Police Cities

传送门

分析

看到这个题我们的第一反应自然是Tarjan缩点，在这之后我们可以发现实际只要在缩点之后所有出度或入度为0的点布置警察局就可以达到要求，我们用dpij表示考虑前i个出度或入度为0的点共布置了j个警察局，s[i]表示这个点原先由几个点构成，tot表示出度或入度为0的点的总数，所以不难得到转移方程

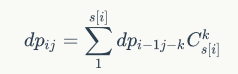
所以不难得到最终答案

注意此题需要使用高精度。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cctype>
#include<cmath>
#include<cstdlib>
#include<queue>
#include<ctime>
#include<vector>
#include<set>
#include<map>
#include<stack>
using namespace std;
#define sp cout<<"---------------------------------------------------"<<endl
struct mint {
      int _[520],__;
};
mint operator + (mint _x,mint _y){
      int _k,_g=0,_i;
      mint _z;
      for(_i=_x.__+1;_i<=512;_i++)_x._[_i]=0;
      for(_i=_y.__+1;_i<=512;_i++)_y._[_i]=0;
      if(_x.__>_y.__)_k=_x.__;
        else _k=_y.__;
      for(_i=1;_i<=_k;_i++){
          _z._[_i]=(_x._[_i]+_y._[_i]+_g)%10;
          _g=(_x._[_i]+_y._[_i]+_g)/10;
      }
      if(_g>0){
          _z._[++_k]=_g;
      }
      _z.__=_k;
      return _z;
}
mint operator * (mint _x,mint _y){
      int _k,_g=0,_i,_j;
      mint _z;
      for(_i=_x.__+1;_i<=512;_i++)_x._[_i]=0;
      for(_i=_y.__+1;_i<=512;_i++)_y._[_i]=0;
      _k=_x.__+_y.__-1;
      for(_i=0;_i<=512;_i++)
        _z._[_i]=0;
      for(_i=1;_i<=_x.__;_i++)
        for(_j=1;_j<=_y.__;_j++)
          _z._[_i+_j-1]+=_x._[_i]*_y._[_j];
      for(_i=1;_i<=_k;_i++){
          int _a=_z._[_i]+_g;
          _z._[_i]=_a%10;
          _g=_a/10;
      }
      while(_g){
        _z._[++_k]=_g%10;
        _g/=10;
      }
      while(_k>1&&_z._[_k]==0)_k--;
      _z.__=_k;
      return _z;
}
mint read(){
      mint _x;
      string _s;
      int _L,_i;
      for(_i=0;_i<=512;_i++)
        _x._[_i]=0;
      cin>>_s;
      _L=_s.length();
      for(_i=1;_i<=_L;_i++)
        _x._[_i]=_s[_L-_i]-'0';
      _x.__=_L;
      return _x;
}
void pr(mint _x){
      int _i;
      for(_i=_x.__;_i>0;_i--)
        printf("%d",_x._[_i]);
      puts("");
}
void test(){
      mint _a,_b;
      _a=read(),_b=read();
      _a=_a+_b;
      pr(_a);
}
int n,m,K,sum,s[110],dfn[110],low[110],ist[110],cnt,belong[110];
int tot,o_d[110],i_d[110],wh[110];
mint dp[110][110],c[110][110];
stack<int>a;
vector<int>o_v[110];
vector<int>v[110];
inline void tarjan(int x){
      dfn[x]=low[x]=++cnt;
      a.push(x);
      ist[x]=1;
      for(int i=0;i<o_v[x].size();i++)
        if(!dfn[o_v[x][i]]){
            tarjan(o_v[x][i]);
            low[x]=min(low[x],low[o_v[x][i]]);
        }else if(ist[o_v[x][i]]){
            low[x]=min(low[x],dfn[o_v[x][i]]);
        }
      if(low[x]==dfn[x]){
          sum++;
        while(1){
          int u=a.top();
          a.pop();
          ist[u]=0;
          s[sum]++;
          belong[u]=sum;
          if(u==x)break;
        }
      }
}
int main(){
      freopen("police.in","r",stdin);
      freopen("police.out","w",stdout);
      int i,j,k;
      //test();
      for(i=0;i<=105;i++)
        for(j=0;j<=105;j++){
          c[i][j]._[1]=0;
          c[i][j].__=1;
        }
      for(i=0;i<=105;i++){
        c[i][0]._[1]=1;
        c[i][0].__=1;
        c[i][i]._[1]=1;
        c[i][i].__=1;
      }
      for(i=1;i<=105;i++)
        for(j=1;j<i;j++)
          c[i][j]=c[i-1][j-1]+c[i-1][j];
      scanf("%d%d%d",&n,&m,&K);
      for(i=1;i<=m;i++){
          int x,y;
          scanf("%d%d",&x,&y);
          o_v[x].push_back(y);
      }
      for(i=1;i<=n;i++)
        if(!dfn[i])tarjan(i);
      for(i=1;i<=n;i++)
        for(j=0;j<o_v[i].size();j++)
          if(belong[i]!=belong[o_v[i][j]]){
              v[belong[i]].push_back(belong[o_v[i][j]]);
              o_d[belong[i]]++;
              i_d[belong[o_v[i][j]]]++;
          }
      int ant=0;
      for(i=1;i<=sum;i++)
        if(!o_d[i]||!i_d[i]){
          tot++;
          wh[tot]=i;
        }else ant+=s[i];
      for(i=0;i<=105;i++)
        for(j=0;j<=105;j++){
          dp[i][j].__=1;
          dp[i][j]._[1]=0;
        }
      dp[0][0]._[1]=1;
      dp[0][0].__=1;
      for(i=1;i<=tot;i++)
        for(j=1;j<=K;j++)
          for(k=1;k<=s[wh[i]];k++)
            dp[i][j]=dp[i][j]+(dp[i-1][j-k]*c[s[wh[i]]][k]);
      mint ans;
      ans.__=1;
      ans._[1]=0;
      for(i=tot;i<=K;i++)
        ans=ans+(dp[tot][i]*c[ant][K-i]);
      pr(ans);
      return 0;
}