p1268 树的重量
题目
树可以用来表示物种之间的进化关系。一棵“进化树”是一个带边权的树,其叶节点表示一个物种,两个叶节点之间的距离表示两个物种的差异。现在,一个重要的问题是,根据物种之间的距离,重构相应的“进化树”。
令N={1..n},用一个N上的矩阵M来定义树T。其中,矩阵M满足:对于任意的i,j,k,有M[i,j] + M[j,k] >= M[i,k]。树T满足:
1.叶节点属于集合N;
2.边权均为非负整数;
3.dT(i,j)=M[i,j],其中dT(i,j)表示树上i到j的最短路径长度。
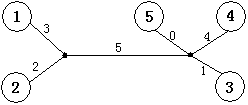
如下图,矩阵M描述了一棵树。

树的重量是指树上所有边权之和。对于任意给出的合法矩阵M,它所能表示树的重量是惟一确定的,不可能找到两棵不同重量的树,它们都符合矩阵M。你的任务就是,根据给出的矩阵M,计算M所表示树的重量。下图是上面给出的矩阵M所能表示的一棵树,这棵树的总重量为15。
输入格式:
输入数据包含若干组数据。每组数据的第一行是一个整数n(2<n<30)。其后n-1行,给出的是矩阵M的一个上三角(不包含对角线),矩阵中所有元素是不超过100的非负整数。输入数据保证合法。
输入数据以n=0结尾。
输出格式:
对于每组输入,输出一行,一个整数,表示树的重量。
分析
我们先考虑n=2的情况,此时答案即为1与2之间的距离。
我们再考虑n=3的情况,如图
我们设两点间距离为T,则插入第3个点所增加的重量即为T23+T13-T12
我们再考虑n=4的情况,如图
我们不难发现因为4与12和3到12有重边,所以我们不能在用12两点的信息来更新4,但我们可以用13或23来更新。所以我们得出一个结论,在增加第i个点所增加的重量是小于i的任意两点所求得的新重量的最小值,即Δans=Min{Tji+Tki-Tjk}。因为n的范围很小,所有我们用三重循环求解即可。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cctype>
#include<cmath>
#include<cstdlib>
#include<queue>
#include<ctime>
#include<vector>
#include<set>
#include<map>
#include<stack>
using namespace std;
int g[1100][1100];
int main()
{ int n,m,i,j,k;
scanf("%d",&n);
while(n){
for(i=1;i<n;i++)
for(j=i+1;j<=n;j++){
scanf("%d",&g[i][j]);
g[j][i]=g[i][j];
}
int ans=g[1][2],sum;
for(i=3;i<=n;i++){
sum=1000000007;
for(j=1;j<i-1;j++)
for(k=j+1;k<i;k++)
sum=min(sum,(g[i][j]+g[i][k]-g[j][k])/2);
ans+=sum;
}
printf("%d\n",ans);
scanf("%d",&n);
}
return 0;
}




