p1983 车站分级

传送门

题目

一条单向的铁路线上，依次有编号为 1,2,…,n的 n 个火车站。每个火车站都有一个级别，最低为 1 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：

如果这趟车次停靠了火车站 x ，则始发站、终点站之间所有级别大于等于火车站 x的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）

例如，下表是 5 趟车次的运行情况。其中，前 4 趟车次均满足要求，而第 5 趟车次由于停靠了 3 号火车站（ 2级）却未停靠途经的 6 号火车站（亦为 2 级）

而不满足要求。

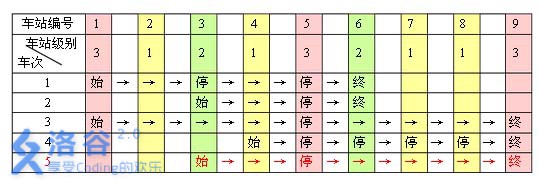
现有 m 趟车次的运行情况（全部满足要求），试推算这 n个火车站至少分为几个不同的级别。

输入格式：

第一行包含 2 个正整数 n,m用一个空格隔开。

第 i+1行 (1≤i≤m)中，首先是一个正整数 si(2≤si≤n) ，表示第 i趟车次有 si个停靠站；接下来有 si ​ 个正整数，表示所有停靠站的编号，从小到大排列。

每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式：

一个正整数，即 n个火车站最少划分的级别数。

分析

这个数据好像有点水...首先我们不难想出在起点与终点之间经过的站点的级数一定比未经过的站点的级数大，所以我们从未经过的站点连一条边指向经过的站点，表示这两个站点之间至少相差一级。之后我们便从入度为0的点出发dfs找最远距离即可。为了优化，我们用一数组记录两站点是否连过边，连过就不连了以防止出边过多。

ps.我曾试图加虚点优化，但反而更慢了，经过思考发现此处虚点优化只对bfs有用，而只会让dfs更慢

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cctype>
#include<cmath>
#include<cstdlib>
#include<queue>
#include<ctime>
#include<vector>
#include<set>
#include<map>
#include<stack>
using namespace std;
int in[1100],cnt,d[1100],ans,len[1100],k,con[1100][1100];
int a[1100];
vector<int>v[1100];
inline void read(int &x){
      int f=1;x=0;
      char s=getchar();
      while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
      while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+(s-'0');s=getchar();}
      x*=f;
}
inline void go(int x){
      int i;
      for(i=0;i<v[x].size();++i)
         if(len[v[x][i]]<len[x]+1){
             len[v[x][i]]=len[x]+1;
             ans=max(ans,len[v[x][i]]);
             go(v[x][i]);
         }
      return;
}
int main()
{     int n,m,i,j,s,e,x,t;
      read(k),read(m);
      cnt=k;
      for(i=1;i<=m;++i){
         read(n);
         memset(in,0,sizeof(in)); 
         s=1100,e=0;
         int sum=0;
         for(j=1;j<=n;++j){ 
            read(a[j]);
            sum++;
            in[a[j]]=1;
            s=min(s,a[j]);
            e=max(e,a[j]);
         }
         if(sum<e-s+1){
           cnt++;
           for(j=s+1;j<e;++j)
             if(!in[j])
               for(t=1;t<=n;++t)
                 if(!con[j][a[t]]){
                   v[j].push_back(a[t]);
                   d[a[t]]=1;
                   con[j][a[t]]=1;
                 }
         }
      }
      for(i=1;i<=k;++i)
         if(!d[i])len[i]=1,go(i);
      printf("%d\n",ans);
      return 0;
}