NOIP2018初赛 解题报告（C++普及）

第24届全国青少年信息学奥林匹克联赛初赛

普及组C++语言试题

竞赛时间：2018 年 10 月 13 日 14:30~16:30

选手注意：

1、试题纸共有 7 页，答题纸共有 2 页，满分 100 分。请在答题纸上作答，写在试题纸上的一律无效。

2、不得使用任何电子设备（如计算器、手机、电子词典等）或查阅任何书籍资料。

一、单项选择题（共15题，每题2分，共计30分；每题有且仅有一个正确选项）

1.以下哪一种设备属于输出设备:( )

A.扫描仪

B.键盘

C.鼠标

D.打印机

解析：

当然是选打印机啦。打印机可以输出图片、文字等。

A.扫描仪是输入设备，可以扫描图像到电脑。

B.键盘也是输入设备，用来输入文字或字母。

C.鼠标也是输入设备，这就不用说了吧。（手动滑稽）

2.下列四个不同进制的数中，与其它三项数值上不相等的是( )。

A. (269)16 (注解：\(2 * 16^2 + 6 * 16^1 + 9 * 16 ^0 = 617\))

B. (617)10

C. (1151)8 （注解：\(1 * 8^3 + 1 * 8^2 + 5 * 8^1 + 1 * 8^0 = 617\)）

D. (1001101011)2 (注解：\(1*2^9+1*2^6+1*2^5+1*2^3+1*2^1+1*2^0=619\))

3.1MB等于( )。

A. 1000 字节

B. 1024 字节

C. 1000 X 1000字节

D. 1024 X 1024字节

注：

1GB=1024MB

1MB=1024KB

1KB=1024B

1B=8b

（B指字节）

4.广域网的英文缩写是( )。

A. LAN 局域网（Local Area Network，LAN)

B. WAN 广域网（WAN，Wide Area Network）

C. MAN man n.男人; 人类; 男子汉; 雇工;vt.使振作; 操纵; 给…配置人员; 在…就位;int.（表示惊讶、气愤等） 嘿，天哪;

D.LNA LNA(低噪声放大器)

5.中国计算机学会于( )年创办全国青少年计算机程序设计竞赛。

A. 1983

B. 1984

C. 1985

D. 1986

注：中国计算机学会于1984年创办全国青少年计算机程序设计竞赛(简称:NOI)

6.如果开始时计算机处于小写输入状态，现在有一只小老鼠反复按照 CapsLock、字母键 A、字母键S、字母键 D、字母键 F 的顺序循环按键，即 CapsLock、A、S、D、F、CapsLock、A、S、D、F、......，屏幕上输出的第 81 个字符是字母 ( )。

A. A

B. S

C. D

D. a

则有序列为：

A S D F a s d f A S D F a s d f ......

八个一循环。

81/8=10...1

故第81个是A。

7.根节点深度为 0，一棵深度为 h 的满 k(k>1)叉树，即除最后一层无任何子节点外，每一层上的所有结点都有k个子结点的树，共有( )个结点。

A. \((k^h+1-1)/(k-1)\)

B. \(k^h-1\)

C. \(k^h\)

D. \((k^h-1)/(k-1)\)

第\(0\)层的节点为\(1\)，第\(1\)层为\(k\)，第二层为\(k^2\)，直到第\(h\)层为\(k^h\)。

则节点数为：

\(1+k^1+k^2+k^3+...+k^h=\frac{1-k^{h+1}}{1-k}1+k\)

即\(\frac{k^{h+1}-1}{k-1}\)
​

8.以下排序算法中，不需要进行关键字比较操作的算法是( )。

A. 基数排序

B. 冒泡排序

C. 堆排序

D. 直接插入排序

基数排序又称桶排序。

比如有这样一个序列：5 3 2 2 1 5

使用基数排序的方法是：

1在这个序列中出现的次数为1

2在这个序列中出现的次数为2

3在这个序列中出现的次数为1

4在这个序列中出现的次数为0

5在这个序列中出现的次数为2

所以该序列排序后为1 2 2 3 5 5

所以基数排序不需要比较，只需要每次把他扔到桶里就好了。

9.给定一个含 \(N\) 个不相同数字的数组，在最坏情况下，找出其中最大或最小的数，至少需要 \(N - 1\) 次比较操作。则最坏情况下，在该数组中同时找最大与最小的数至少需要( )次比较操作。(\(\lceil\rceil\)表示向上取整，\(\lfloor\rfloor\)表示向下取整)

A \(\lceil3N/2\rceil-2\)

B \(\lfloor3N/2\rfloor-2\)

C. 2N - 2

D. 2N - 4

答案：A

10.下面的故事与( )算法有着异曲同工之妙。从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事:“从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事:‘从前有座山，山里有座庙，庙里有个老和尚给小和尚讲故事......’”

A. 枚举

B. 递归

C. 贪心

D. 分治

答案：B

这是一种递归，不断得套自己。

11.由四个没有区别的点构成的简单无向连通图的个数是( )。

A. 6

B. 7

C. 8

D.9

答案：A

简单图：设G=(V，E)是图，若G中既无吊环又无多重边，则称G是简单图(simplegraph)

——by abc2237512422

12.设含有 10 个元素的集合的全部子集数为 S，其中由 7 个元素组成的子集数为T，则T / S的值为( )。

A. 5 / 32

B. 15 / 128

C. 1 / 8

D. 21 / 128

\(T=C^7_{10}=C^3_{10}=120\)

\(S=C^0_{10}+C^1_{10}+C^2_{10}+...+C^{10}_{10}=1024\)

那么

\(T/S=120/1024=15/128T/S=120/1024=15/128\)

13.10000以内，与10000互质的正整数有( )个。

A. 2000

B. 4000

C. 6000

D. 8000

这道题用到了容斥。

首先看与10000是因数关系的是2或5的倍数。

所以可将2或5的倍数的个数减去10的倍数个数。

最后将10000减去上所求的个数即得互质的个数。

14.为了统计一个非负整数的二进制形式中 1 的个数，代码如下:

int CountBit(int x)
{
int ret = 0;
while (x)
{
ret++;
___________;
}
return ret;
}

则空格内要填入的语句是( )。

A. x >>= 1

B. x &= x - 1

C. x |= x >> 1

D. x <<= 1

选B。

为了统计一个非负整数的二进制形式中 1 的个数

所以每次就删掉最高位（第一个为1的那一位）。

15.下图中所使用的数据结构是( )。

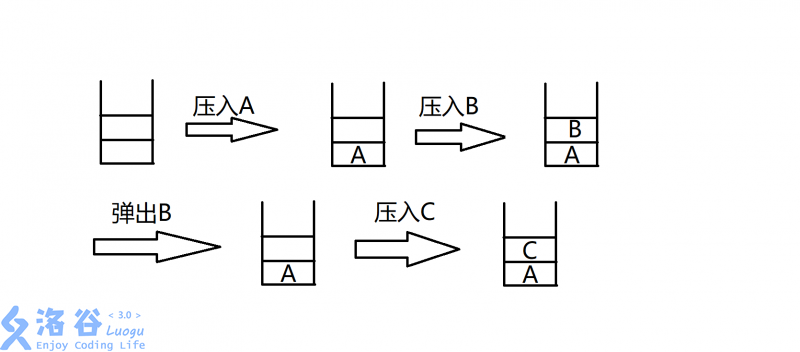
洛谷丑陋的水印↑

A. 哈希表

B. 栈

C. 队列

D. 二叉树

这道题模拟的是先进先出的数据结构——栈

不会的自己温故一下百度百科

二、问题求解（共 2 题，每题 5 分，共计 10 分）

1.甲乙丙丁四人在考虑周末要不要外出郊游。 已知

(1)如果周末下雨，并且乙不去，则甲一定不去；

(2)如果乙去，则丁一定去；

(3)如果丙去，则丁一定不去；

(4)如果丁不去，而且甲不去，则丙一定不去。

如果周末丙去了，则甲(去了/没去)(1 分)，乙(去了/没去)(1 分)，丁(去了/没去)(1 分)，周末(下雨/ 没下雨)(2 分)。

这道题貌似是小学奥数题吧（2333333333333）。

只需要枚举一遍，看一看是否矛盾就好了。

首先，丙是要去的。

那么根据(4)可以得知丁、甲中一定有一个或两个去。

而又根据(3)可以得知丁不去，那么甲去。

又根据(2)，因为前面已经提到：丁不去。

那么证明乙也不去。

最后根据(1)得知，周末一定不下雨，如果下雨，那么甲也不去，就和之前的矛盾了。

所以答案：

甲（去了） 乙（没去） 丁（没去） 周末（没下雨）

2.从 1 到 2018 这 2018 个数中，共有544个包含数字 8 的数。

包含数字 8 的数是指有某一位是“8”的数，例如“2018”与“188”。

数码问题

1-99有19个

100-199有19个

......

800-899有100个

1800-1899有100个

一共有:

\(（20-2）×19+2×100+2\)

\(=18×19+202\)

\(=342+202\)

\(=544\)个

三、阅读程序写结果（共 4 题，每题 8 分，共计 32 分）

#include<cstdio>
char st[100];
int main() {
     scanf("%s", st);
     for (int i = 0; st[i]; ++i) {
       if ('A' <= st[i] && st[i]<= 'Z')
         st[i] += 1;
     }
     printf("%s\n", st);
     return 0;
}

输入：QuanGuoLianSai

输出：RuanHuoMianTai

这道题也就是将所有的大写字母往后一位（+1）

#include<cstdio>
int main() {
     int x;
     scanf("%d", &x);
     int res = 0;
     for (int i = 0; i < x; ++i) {
       if (i * i % x == 1) {
        ++res;
        }
  }
     printf("%d", res);
return 0;
}

输入：15

输出：4

给出的数据很小，直接模拟一遍就好啦。

#include<iostream>
using namespacestd;
int n, m;
int findans(int n, int m) {
if (n == 0) return m;
if (m == 0) return n % 3;
return findans(n - 1, m) - findans(n, m - 1) +findans(n - 1, m - 1);
}
int main(){
cin >> n >> m;
cout << findans(n, m) << endl;
return 0;
}

输入：5 6

输出：8

通过递归就可想到可以使用递推来解决。
所以画一个矩阵就好了。

\(f[0][i]=i;\)
\(f[i][0]=i \mod 3\)

\(f[i][j]=f[i−1][j]−f[i][j−1]+f[i−1][j−1]\)

excel真方便（逃：

#include<cstdio>
int n, d[100];
bool v[100];
int main() {
     scanf("%d", &n);
     for (int i = 0; i < n; ++i) {
       scanf("%d", d + i);
       v[i] = false;
     }
     int cnt = 0;
     for (int i = 0; i < n; ++i) {
       if (!v[i]) {
         for (int j = i; !v[j]; j = d[j]) {
        v[j] = true;
        }
        ++cnt;
        }
     }
     printf("%d\n", cnt);
     return 0;
}

输入：10 7 1 4 3 2 5 9 8 0 6

输出：6

按题意模拟即可，数据很小，但注意第一个读入的数据为n。

四、完善程序（共 2 题，每题 14 分，共计 28 分）

1.（最大公约数之和）下列程序想要求解整数的所有约数两两之间最大公约数的和对10007求余后的值，试补全程序。（第一空 2 分，其余 3 分）

举例来说，4的所有约数是1,2,4。1和2的最大公约数为1；2和4的最大公约数为2；1和4的最大公约数为1。于是答案为1 + 2 + 1 = 4。

要求 getDivisor 函数的复杂度为0(√n)，gcd 函数的复杂度为O(log max(a, b))。

#include<iostream>
using namespacestd;
const int N =110000, P = 10007;
int n;
int a[N], len;
int ans;
void getDivisor(){
    len = 0;
    for(int i=1;__(1)__<=n;++i)
        if (n % i == 0) {
            a[++len] = i;
            if(__(1)__!=i)a[++len]=n/i;
        }
    }
}
int gcd(int a,int b) {
    if (b == 0) {
        __(3)__;
    }
    return gcd(b,__(4)__);
}
int main() {
    cin >> n;
    getDivisor();
    ans = 0;
    for (int i = 1; i <= len; ++i) {
        for (int j = i + 1; j <= len; ++j) {
            ans=(__(5)__)%P;
        }
    }
    cout << ans << endl;
    return 0;
}

答案：i*i , n/i , return a, a%b , ans+gcd(a[i],a[j])

这道题先求出所有的约数，然后两两求最大公约数，注意%P;

2.对于一个1到n的排列p(即1到n中每一个数在p中出现了恰好一次)，令qi为第i个位置之后第一个比pi值更大的位置，如果不存在这样的位置，则qi =n+1。

举例来说，如果n=5且p为1 5 4 2 3，则q为2 6 6 5 6。

下列程序读入了排列p，使用双向链表求解了答案。试补全程序。（第二空2分，其余3分）

数据范围 1 ≤ n ≤ 105。

#include<iostream>
using namespace std;
const int N =100010;
int n;
int L[N], R[N],a[N];
int main() {
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        int x;
        cin >> x;
        __(1)__;
    }
    for (int i = 1; i <= n; ++i) {
        R[i]=__(2)__;
        L[i] = i - 1;
    }
    for (int i = 1; i <= n; ++i) {
        L[__(3)__]= L[a[i]];
        R[L[a[i]]] = R[__(4)__];
    }
    for (int i = 1; i <= n; ++i) {
        cout <<__(5)__<<" ";
    }
    cout << endl;
    return 0;
}

这道题用双向链表解答。。。

答案：a[x]=i , i+1 , R[a[i]] , a[i] , R[i]