什么是栈?
我们以一副生动的图来类比这个过程
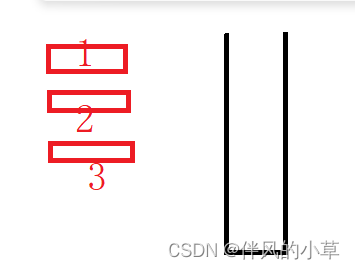
这些红色方块想要放入这个黑色桶里
红色方块就是元素,黑色桶就是Stack,栈
不难想象出,从桶里拿出方块是拿最顶上的,放入也是只能放到最顶上
我们把这个拿取的过程叫出栈(Pop),放入叫压栈/入栈/进栈(Push)
我们把开口的一端叫栈顶,不开口一段叫栈底
遵循“后入先出”(LIFO原则)的规则
如何实现一个栈?
一般来讲:
- 用数组等顺序表实现的栈叫顺序栈
- 用链表实现的栈叫链栈
顺序栈
struct Stack
{
int data[MAX_SIZE];
int top; // 栈顶指针,指向栈顶元素的索引
};
// 初始化栈
void initStack(struct Stack* stack)
{
stack->top = -1; // 初始化栈顶指针为-1表示栈为空
}
// 检查栈是否为空
int isEmpty(struct Stack* stack)
{
return stack->top == -1;
}
// 检查栈是否已满
int isFull(struct Stack* stack)
{
return stack->top == MAX_SIZE - 1;
}
// 入栈操作
void push(struct Stack* stack, int value)
{
if (isFull(stack))
{
printf("栈已满,无法入栈\n");
return;
}
stack->top++;
stack->data[stack->top] = value;
}
// 出栈操作
int pop(struct Stack* stack)
{
if (isEmpty(stack))
{
printf("栈为空,无法出栈\n");
return -1; // 返回一个特殊值表示出错
}
int value = stack->data[stack->top];
stack->top--;
return value;
}
// 获取栈顶元素的值
int peek(struct Stack* stack)
{
if (isEmpty(stack))
{
printf("栈为空\n");
return -1; // 返回一个特殊值表示出错
}
return stack->data[stack->top];
}
链栈
// 定义链表节点结构
struct Node
{
int data;
struct Node* next;
};
// 定义链栈结构
struct Stack
{
struct Node* top; // 栈顶指针
};
// 初始化链栈
void initStack(struct Stack* stack)
{
stack->top = NULL;
}
// 检查链栈是否为空
int isEmpty(struct Stack* stack)
{
return stack->top == NULL;
}
// 入栈操作
void push(struct Stack* stack, int value)
{
// 创建新节点
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
if (newNode == NULL)
{
printf("内存分配失败\n");
exit(1);
}
// 设置节点数据和指针
newNode->data = value;
newNode->next = stack->top;
// 更新栈顶指针
stack->top = newNode;
}
// 出栈操作
int pop(struct Stack* stack)
{
if (isEmpty(stack))
{
printf("栈为空,无法出栈\n");
return -1; // 返回一个特殊值表示出错
}
// 获取栈顶节点
struct Node* topNode = stack->top;
int value = topNode->data;
// 更新栈顶指针
stack->top = topNode->next;
// 释放栈顶节点的内存
free(topNode);
return value;
}
// 获取栈顶元素的值
int peek(struct Stack* stack)
{
if (isEmpty(stack))
{
printf("栈为空\n");
return -1; // 返回一个特殊值表示出错
}
return stack->top->data;
}
// 销毁链栈
void destroyStack(struct Stack* stack)
{
while (!isEmpty(stack))
{
pop(stack);
}
}
在入栈的时候,我们要把top的值更新,然后把这个值加到vals的末尾,修改capacity+1
在出栈的时候,我们要更新top,然后从vals末尾移除这个值,修改capacity-1
capacity不只是容量,也是一种索引,记录在vals中的位置
在没有元素时,Top指针一般为-1,在有元素时,一般指向栈顶元素
栈内没有元素称为”空栈“
双向栈

相似的,我们还是可以从top的位置去拿元素,放元素,只不过这次我们需要决定从哪边拿这个元素
当一个栈元素多,一个栈元素少的时候,我们就可以这样去写,让一个栈可以占用另一个栈的空间,提高空间的利用率
大家可能会疑惑,为什么不写两个栈,可是那样就会开辟两块空间不是吗?如果栈1满了,我们一般就会把它翻倍,何不利用其他闲置的空间呢?
struct Stack
{
//左侧顶上的元素
int top1;
//右侧顶上的元素
int top2;
//存数据的数组
int* vals;
//数组总容量
int valSize;
//左侧容量
int capacity1;
//右侧容量
int capacity2;
}
是不是还是一样的,我们只需要把
但是万物不可能只有优点,双向栈可能会让两个top相遇,这个时候就会上溢,而且这样的双向结构,如果发送这样的问题,我们只能去为数组扩容,然后把整个后部分后移
栈与递归的关系
函数递归层数过多时,会引发栈溢出异常,我们需要拆解为非递归形式。
绝大多数函数递归都能拆解为非递归形式,而这个媒介就是栈。
例如 A(i)递归调用A(i+1)
那么我们就可以令i入栈
此时栈内只有一个i元素
然后循环执行以下过程:
- 出栈一个元素
- 计算下一个元素i+1,入栈这个元素
- 执行对i的操作
直到栈空即可。
同理,我们也能通过栈实现树的遍历,有分支的递归等。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号