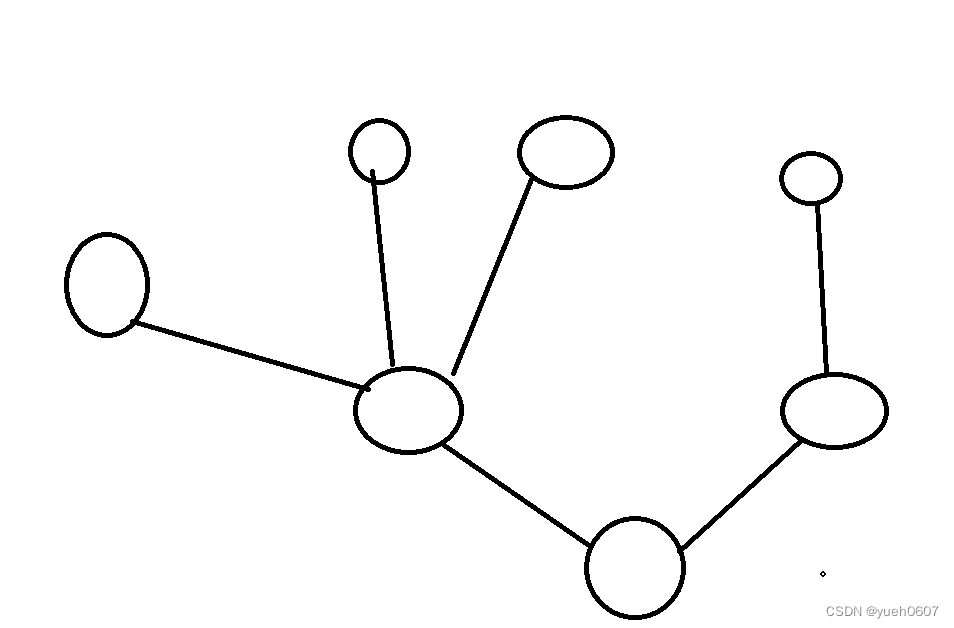
在这里插入图片描述
它是不是像一棵树？
对于一个树而言，我们先介绍一个概念

  1. 每个节点有0个子节点或者大于0的任意个；
  2. 没有父节点的节点称为根节点；
  3. 每一个非根节点有且只有一个父节点；
  4. 除了根节点外，每个子节点可分为多个不相交的子树；

二叉树

简而言之，只能有两个树杈
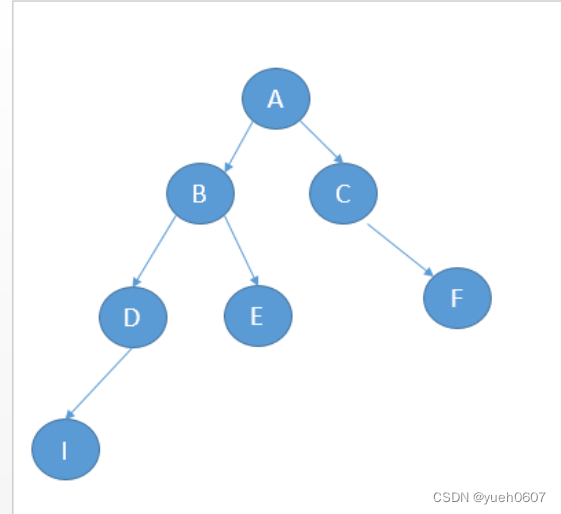
在这里插入图片描述

二叉树的概念

一个节点最多有两个子节点的树

在这里插入图片描述

二叉树的存储

第一种是采取类似链表的形式

struct BinaryTree
{
	struct BinaryTree* leftChild;
	struct BinaryTree* leftChild;
	
	int val;
}

不难理解这种思路类似于LinkedList。

第二种是用顺序表去存
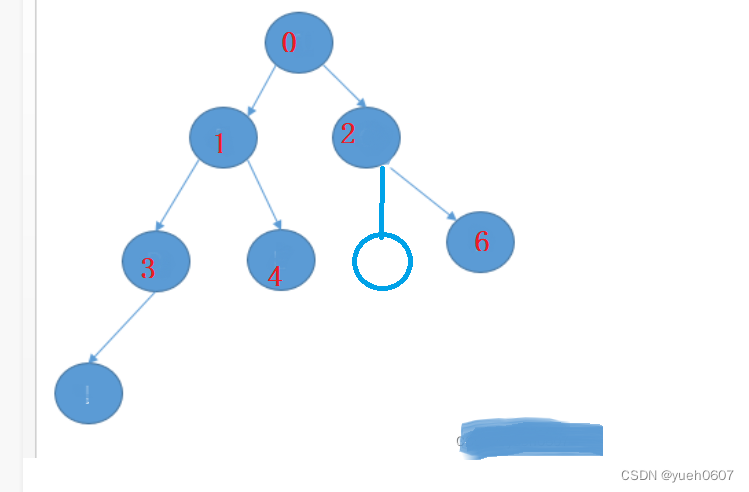
在这里插入图片描述
给树节点加上编号，
在这里插入图片描述
有一个公式，假如我们已知父节点在数组里的索引编号，那就能得到数组里的
leftChild = i * 2
rightChild = i * 2 + 1

我们可以验证一下，假如已知1号TreeNode，index = 1
left = 3，数组index = 3
right = 4.数组index = 4
多说都是数学的泪…且行且珍惜

前中后序遍历

二叉树有良好的递归性
因为我们给出任意一个节点，都知道下面可能有两个节点，所以从根节点开始，它的两个子节点就能视作一颗新的二叉树，通过递归让问题得到无限简化，直到只有一个节点本身

我们直接研究递归问题的每一次，将问题简单化

遍历的顺序是怎么样的？
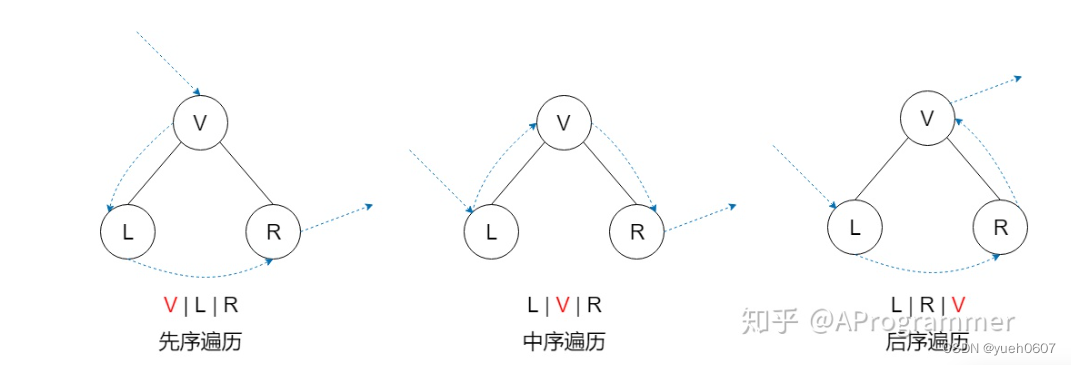
在这里插入图片描述
是什么序，取决于父节点所处的位置，就三个节点的而言，父节点先遍历就是先序，第二个是中序，最后是后序
先序：父 - 左 -右
中序：左 - 父 -右
后序：左 - 右 -父

对于上文实现的的BinaryTree节点结构，我们只需要写递归函数去遍历就可以了

对于用顺序表模拟的树，我们还是这样想，拿到某个节点的下标，直接用上文的公式反推或者顺推就能找到下一个节点，算法上并无太大难度。

如果我们想非递归实现这些遍历，以前序为例，我们使用栈（Stack）实现，在之前的文章中我们说过绝大多数递归都能转为使用栈的非递归形式：
1.定义一个栈并初始化
2.判断二叉树是否为空，不为空，则将根节点入栈。
3.当栈不为空时，循环下列内容

-  栈顶元素退栈并访问该节点
-  栈顶右子节点进栈
-  栈顶左子节点进栈

#include <stdio.h>
#include <stdlib.h>

// 定义二叉树节点结构
struct TreeNode 
{
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
};

// 创建新节点
struct TreeNode* createNode(int data) 
{
    struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    newNode->data = data;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

// 前序遍历
void preorderTraversal(struct TreeNode* root) 
{
    if (root != NULL) 
    {
        printf("%d ", root->data);
        preorderTraversal(root->left);
        preorderTraversal(root->right);
    }
}

// 中序遍历
void inorderTraversal(struct TreeNode* root) 
{
    if (root != NULL) 
    {
        inorderTraversal(root->left);
        printf("%d ", root->data);
        inorderTraversal(root->right);
    }
}

// 后序遍历
void postorderTraversal(struct TreeNode* root) 
{
    if (root != NULL) 
    {
        postorderTraversal(root->left);
        postorderTraversal(root->right);
        printf("%d ", root->data);
    }
}

非递归实现就不给出了，思路很简单

层次遍历

还有一种叫层次遍历，从名字听得出来，逐层遍历，从上到下，从左到右
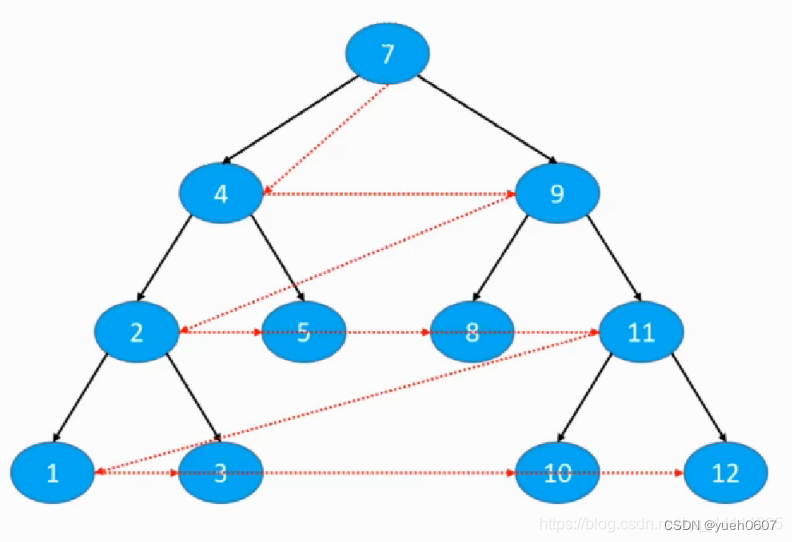
在这里插入图片描述

遍历过程很简单：

  • 根节点入队

  • 循环执行以下内容：

    • 出队一个元素并执行操作
    • 把出队的元素的子节点入队

前驱和后继

1.元素的前驱与后继
数据结构中，每个数据个体被称为“数据元素”（简称“元素”），每个元素都有前驱和后驱(不含首尾)。

2.前驱
某一元素的左侧相邻元素称为“直接前驱”，位于此元素左侧的所有元素统称为“前驱元素”。

2.后继
某一元素的右侧相邻元素称为“直接后继”，位于此元素右侧的所有元素统称为“后继元素”。

3.二叉树的前驱后继
前驱节点：对一棵二叉树进行中序遍历，遍历后的顺序，当前节点的前一个节点为该节点的前驱节点；

后继节点：对一棵二叉树进行中序遍历，遍历后的顺序，当前节点的后一个节点为该节点的后继节点；