声明:本文为作者高一下学期所写,无改动,进了垃圾箱,发出来仅用作年少轻狂的纪念,当时太过大言不惭了,文中也可能有错误。当时作者在高一,自学的复数之类的,写下了这篇文章。
绝对没有装x和标题党的意思…谢谢体谅
矩阵,欧拉角,四元数旋转优缺点对比
1. 欧拉角
- 优点:三个角度组成,直观,容易理解。
- 优点:可以进行从一个方向到另一个方向旋转大于180度的角度。
- 弱点:万向节锁问题
- 缺点:转换为3个3*3的矩阵,效率低,存储空间大
2. 四元数
由四个数字(在Unity中称为x,y,z和w)组成,然而这些数字不表示角度或轴,就像不要在Unity中直接给transform.rotation赋值四元数,除非你对四元数掌握十分清晰
- 优点:四元数旋转不存在万向节锁问题。
- 优点:存储空间小,计算效率高。
- 缺点:单个四元数不能表示在任何方向上超过180度的旋转。
- 缺点:四元数的表示不直观。
3. 旋转矩阵
- 优点:不存在万向节锁问题
- 优点:可以表示围绕任意轴的旋转,四元数的旋转轴均为通过物体中心点的轴,矩阵则不受此限制
- 缺点:矩阵旋转使用4x4矩阵,记录16个数值,四元数只需要4个数值。计算较复杂,效率较低。
前言
笔者在使用Unity3D引擎过程中碰到了做人物旋转的内容,当时IDE弹出来四元数,有点手足无措,按照四元数的xyzw四个轴,给xyz赋值了欧拉角,当时人物一顿抽搐…咳咳
笔者又找了很多资料,发现四元数是简单超复数,四维概念
当时就放弃了,当然这是一年前的事情了
笔者目前是高一在校学生,对于高二学习的一些数学概念还不是很清晰,所以更不用提高等数学和线性代数的内容了,一片糊涂
所以笔者请教了一些对四元数或数学有一定认知的前辈,了解了四元数的一些相关知识,写下这篇文章分享给所有人包括和我一样在初高中就热爱软件的朋友们
对比以上优点缺点,本文主要研究四元数的认知,不包括如何进行的旋转
- 另外本文的所有蓝色字体包括标题均为超链接,可点击获取相关内容
一. 复数
四元数是简单超复数,这是百度百科给出的定义
所有我们得先从复数说起,因为笔者数学知识实在有限,只能按照自己的理解和网络资源进行阐述,如果看不懂笔者的叙述可以点击超链接跳转到相关文档
复数其实我们见过的,就像方程的根判别式 b²-4ac判定没有实数根的时候,但是他有复数根
定义
我们把形如 z = a + b i(a,b均为实数)的数称为复数,其中a称为实部,b称为虚部,
i 称为虚数单位。当 z的虚部等于零时,常称z为实数;当z的虚部不等于零时,实部等于零时,常称z为虚数。
也就代表这个Z就是复数,复数就是实数+虚数,当实数部分等于0时复数就变成了虚数,当虚数部分等于0,复数就变成实数,什么单位之类的反正我看不懂
复平面

没错…他就是个平面,只不过他叫复平面
表示复数用的平面,所以复数可以在上面表示
这个平面的特点就是横轴表示实数,纵轴表示虚数,
而且跟我们平常的坐标系不同的是,纵轴的单位是 i
而不是1,横轴没区别,就如下图所示
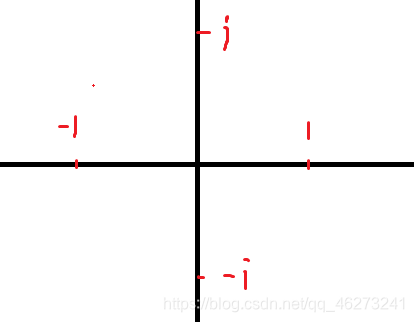
为什么纵轴是i,上面说过了,纵轴的单位是i,2333333
怎么表示一个复数呢?当然是横纵坐标,横轴实数,纵轴虚数,实数+虚数就是复数了
看这个例子
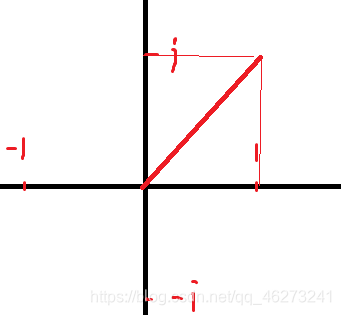
这个点所表示的复数就是 z = 1 + i
可见复数表示在这个平面上就是坐标的xy之和
这也是复平面坐标变成复数的法则
逻辑推理
那么问题来了,
( 1,0) * -1 = (-1,0)
这是为什么呢,乘-1就会翻转方向,这是向量的性质
1 * -1 = -1
然后
-1 = -1 + 0i => (-1,0)
根据上面的法则展开之后这个也是成立的
我们可以猜测复数在复平面内有向量的性质
我认为复数在复平面内有两种表示形态
1.向量
2.代数式
这就是以上探究得到的重要内容
- 复数在复平面内有两种表示形态,分别是向量和代数式
- 两种形态支持互换
向量的x,y相加就是代数式形态,代数式的实数部和虚数部可分解为向量形态
也就是 a + bi => (a,bi) ,可以表示复数并且相互转换
回到原来的内容, 从(1,0)这个方向旋转到(-1,0)这个方向,是180度,这个操作乘的是 -1
那我们不妨试试乘 i会有什么结果呢?
还是这个(1,0),

要进行运算,我们需要展开向量
(1,0) => 1 + 0i 也就是1
这个复数也就是1,乘 i 之后结果是 i
i => (0 + i) => (0,i)
我们算出来(1,0) * i的结果是(0,i)
再结合坐标轴

可以看出,向量的方向旋转了90°
显然,再乘 i 会翻转180°
而(1,0) * -1 = (-1,0)的效果也是翻转180°
所以乘两次 i 和乘-1的结果是相同的
那么我们得到 < i * i = -1>
这个结论对论证下文的旋转有重要作用
如果你到现在还没理解以上内容,那么你可能需要回头看看,或者自行学习复数相关知识,否则对下文的理解将会愈发困难。笔者只是个高一学生,没有什么讲授的经验,自身也不是很了解复数,学不会也是很正常的.
普遍规律
接下来
我们讨论普遍规律
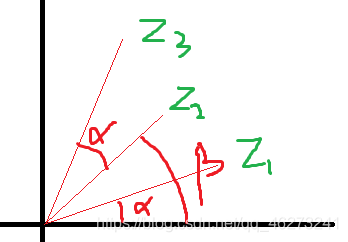
如图是一个复平面,纵轴的单位还是i,横轴还是1
图中有三条线,分别表示三个复数,
现在我想把 Z2 所代表的线 逆时针旋转α角 到达Z3
假定 Z1 与X轴夹角为α
假定 Z2 与X轴夹角为 β
那么 Z3 与X轴夹角就是 α+β
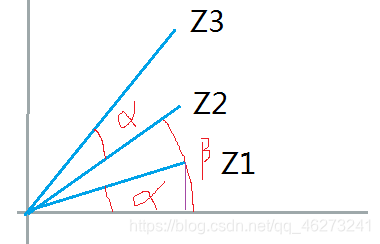
OK,我们换个好图
我们思考为什么一个复数乘另一个复数就可以旋转呢?
就像(1,0) *(0,i)就旋转了90度到了位置(0,i),上文是乘 i,但是 i 可以写为复数向量的形式
类比验证
(0,i)是(1,0)旋转(0,i)角得到的
Z3 是 Z2 逆时针旋转α角度,也就是旋转 ∠Z1 大小得到的
(0,i)可以看做(1,0)* (0,i)产生的旋转
那么如上图,Z3 是不是也可以看做 Z2 * Z1 所产生的旋转呢(Z表示复数)
我们需要设一些量
设
Z1的模长为r1
Z2的模长为r2.
(以下Zn与X轴夹角均简写为∠Zn的形式)
- 角相加,则模长乘积,显然 ∠Z3 = ∠Z1 + ∠Z2
Z3的模长可以求出为r1 * r2
模长可以理解成长度
那么我们先写出Z1,Z2,Z3的向量形式,还是因为纵轴单位是 i,必须乘基础单位
就像(x,y)完全就是简写形式,因为常规的坐标轴单位就是1,能省略
他的完整形式是(x * 1,y * 1)
Z1(r1 cosα,r1 sinα i)
Z2(r2 cosβ,r2 sinβ i)
Z3(r1r2 cos(α+β),r1r2 sin(α+β) i)
在∠Z3 = ∠Z1 + ∠Z2成立时
那么,如果Z3 = Z1 * Z2成立,说明我们得到了一个普遍的规律
一个复数如果想在复平面内旋转任意角,只需要将这个复数乘任意角的复数形式
就像Z2想旋转Z1,就乘了Z1得到Z3
(语言可能不标准)
那么我们需要证明这个结论是真还是假,
- 在∠Z3 = ∠Z1 + ∠Z2成立时
- Z3 = Z1 * Z2
结合上面我们写出的Z1 - Z3的向量形式,转变成代数式
Z3 = Z1 * Z2
防止部分人遗忘两角和差公式
cos (α+β) = cosα cosβ - sinα sinβ
sin (α+β) = sinα cosβ + sinβ cosα
接着证明可以变成以下代数式
r1r2 cos(α+β) + r1r2 sin(α+β) i = (r2 cosβ + r2 sinβ i)(r1 cosα + r1 sinα i)
根据两角和差公式和乘法分配律
r1r2(cosα cosβ - sinα sinβ)+ r1r2(sinα cosβ + sinβ cosα)i = r1r2 (cosα cosβ + sinα cosβ i + sinβ cosα i + sinα sinβ i2 )
因为前面证明过 i2 = -1这里就能进行代换
并且**r1r2**可以约掉了
(cosα cosβ - sinα sinβ)+ (sinα cosβ + sinβ cosα)i = (cosα cosβ + sinα cosβ i + sinβ cosα i - sinα sinβ )
(cosα cosβ - sinα sinβ)+ (sinα cosβ + sinβ cosα)i = (cosα cosβ - sinα sinβ + sinα cosβ i + sinβ cosα i )
(cosα cosβ - sinα sinβ)+ (sinα cosβ + sinβ cosα)i =(cosα cosβ - sinα sinβ)+ (sinα cosβ + sinβ cosα)i
这样就完成了证明
- 在∠Z3 = ∠Z1 + ∠Z2成立时
- Z3 = Z1 * Z2
这为我们后面对四元数的认知打下了坚实基础
四元数理解
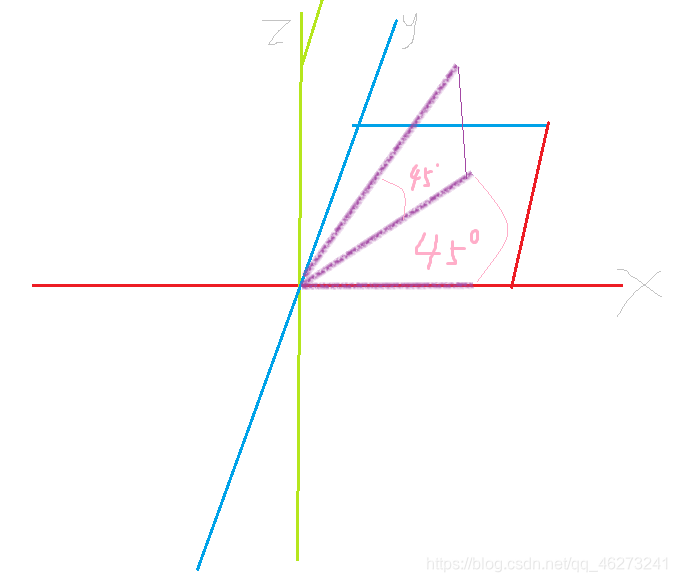
如图,一个三维旋转
我们要做的是把x轴上的一条线旋转到xy平面上,这是前面提到的二维旋转
然后再组合为空间旋转,这个过程需要两个复数来表示
前面也说过四元数是简单超复数,其实四元数也可以理解为复数的复数
按照数学上的语言说,它只满足分配率而丧失了结合律
而更复杂的八元数连分配率也丧失了
好了,回到正题,讨论这个空间旋转
我们先看四元数的表达式
Q = a + bi + cj + dk
其中abcd均为实数,a为四元数实部
ijk为虚数,bi,cj,dk为四元数虚部,
之前我们求出了复数描述二维旋转时,i2 = -1
类似的,四元数也有这类性质
i,j,j都满足
i2=j2=k2= -1
ij=k、ji=-k、jk=i、kj=-i、ki=j、ik=-j
这样的分解做法和欧拉角十分类似…
甚至我自己都怀疑这是不是弯路
设在X轴上的那根线是r1,xy平面上那个是r2
则 有如下
Z1(r1,0)
Z2(r2 cos 45°,r2 sin 45°)
Z3 = Z2 = Z1 * Z2 (因为从x轴旋转的话和旋转量Z2是一致的)
Z4等下探究
然后我们做的旋转操作就是
Z1 * Z2
Z1是初始量
Z3 = Z1 * Z2 = r1 (r2 cos 45° + r2 sin 45°)
是不是要写Z4了,可是,别忘了,这是两个平面,轴也有改变
所以,我认为这个Z3整个就是第二次旋转的X轴了
Z4 [r1 (r2 cos 45° + r2 sin 45°),0]
Z5 (r3 cos 45°,r3 sin 45°)
写到这里,我也是忐忑的。如果真的不对,这6000个字符就白写了
Z = [r1 (r2 cos 45° + r2 sin 45°),0](r3 cos 45°,r3 sin 45°)
这不是开始的量和两个旋转量的积吗
所以,可能四元数就是两个复数的积,因为他丢失了一些乘法运算的法则,显得有顺序性
我们验证一下四元数有无可能是复数积
这里的abjki都是一种表示形式,上下文不是同一个量,主要看形式
Z1 = a + bi
Z2 = c + dk
相乘看看
Z1 * Z2 = ac + adk + cbi + bdki
分析看看,ac是实数,ad为实数,cb是实数,bd是实数
k,i,ki都是虚数
正好满足
Q = a + bi + cj + dk
其1实三虚之和的形式符合
但是,上面我们说了,四元数性质 ,ki = j另一个虚数
就引入了第三个字母,所以该式确实就是四元数
但是不代表四元数就可以这样分解来运算,这个只是说明两个复数乘积就是四元数,但是不一定是四元数相乘的法则
那么一个四元数乘另一个四元数就可以表示旋转是正确的
经过我了解,四元数不符合乘法交换律,也就是它有序

四元数乘法没法这样交换算
后来我也找到了资料,四元数元素对乘表示旋转的积分
这个东西已经超出了我的理解范围

以上内容主要是为了对四元数有一个合理的认知
复数可以表示二维,
至于为什么三元数不能表示三维,而用了四元数,道理有点深,建议看这个,还讨论的八元数的存在性
《关于四元数的讨论》
旋转并不是直接乘一个四元数就能达到目的的,还要进行一些处理,
四元数乘法会产生多个效果,其中一个就是我们的旋转操作
详细的内容下一篇文章分享



 浙公网安备 33010602011771号
浙公网安备 33010602011771号