游戏开发初等数学基础

凑数图()

立体图形面积体积

1. 立方体（Cube）:

• 表面积公式: $6a^2$ （其中 $a$ 是边长）。
• 体积公式: $a^3$ （其中 $a$ 是边长）。

2. 球体（Sphere）:

• 表面积公式: $4\pi r^2$ （其中 $r$ 是半径）。
• 体积公式: $\frac{4}{3}\pi r^3$ （其中 $r$ 是半径）。

3. 圆柱体（Cylinder）:

• 表面积公式（侧面和两个底面总和）: $2\pi rh+2\pi r^2$ （其中 $r$ 是底面半径，$h$ 是高度）。
• 体积公式: $\pi r^{2}h$ （其中 $r$ 是底面半径，$h$ 是高度）。

4. 锥体（Cone）:

• 表面积公式（侧面和底面总和）: $\pi r(r+\sqrt{r^2+h^2})$ （其中 $r$ 是底面半径，$h$ 是高度）。
• 体积公式: $\frac{1}{3}\pi r^{2}h$ （其中 $r$ 是底面半径，$h$ 是高度）。

5. 圆环（Torus）:

• 表面积公式: $4{\pi }^{2}Rr$ （其中 $R$ 是大半径，$r$ 是小半径）。
• 体积公式: $2{\pi }^{2}R{r}^2$ （其中 $R$ 是大半径，$r$ 是小半径）。

平面图形面积与周长

1. 矩形（Rectangle）:

• 面积公式: $A=l\cdot w$ （其中 $l$ 是长度，$w$ 是宽度）。
• 周长公式: $P=2(l+w)$ （其中 $l$ 是长度，$w$ 是宽度）。

2. 正方形（Square）:

• 面积公式: $A=a^2$ （其中 $a$ 是边长）。
• 周长公式: $P=4a$ （其中 $a$ 是边长）。

3. 圆（Circle）:

• 面积公式: $A=\pi r^2$ （其中 $r$ 是半径）。
• 周长公式: $P=2\pi r$ （其中 $r$ 是半径）。

4. 三角形（Triangle）:

• 面积公式: $A=\frac{1}{2}bh$ （其中 $b$ 是底边长，$h$ 是高度）。
• 周长公式: $P=a+b+c$ （其中 $a$、$b$、$c$ 是三边长度）。

5. 梯形（Trapezoid）:

• 面积公式: $A=\frac{1}{2}(a+b)h$ （其中 $a$ 和 $b$ 是上下底边长，$h$ 是高度）。
• 周长公式: $P=a+b+c+d$ （其中 $a$、$b$、$c$、$d$ 是各边长度）。

6. 圆环（Annulus）:

• 面积公式: $A=\pi (R^2-r^2)$ （其中 $R$ 是外圆半径，$r$ 是内圆半径）。
• 周长公式: $P=2\pi (R+r)$ （其中 $R$ 是外圆半径，$r$ 是内圆半径）。

三角函数

1. 两角相加的三角函数公式：

• $\sin (A+B)=\sin (A)\cos (B)+\cos (A)\sin (B)$
• $\cos (A+B)=\cos (A)\cos (B)-\sin (A)\sin (B)$
• $\tan (A+B)=\frac{\tan (A)+\tan (B)}{1-\tan (A)\tan (B)}$

2. 两角差的三角函数公式：

• $\sin (A-B)=\sin (A)\cos (B)-\cos (A)\sin (B)$
• $\cos (A-B)=\cos (A)\cos (B)+\sin (A)\sin (B)$
• $\tan (A-B)=\frac{\tan (A)-\tan (B)}{1-\tan (A)\tan (B)}$

3. 二倍角的三角函数公式：
注意这三个公式以及下面的半角公式能轻而易举的被上述的两角和差公式推导
根据需要记忆即可

• $\sin (2A)=2\sin (A)\cos (A)$
• $\cos (2A)={\cos }^2(A)-{\sin }^2(A)=2{\cos }^2(A)-1=1-2{\sin }^2(A)$
• $\tan (2A)=\frac{2\tan (A)}{1-{\tan }^2(A)}$

4. 半角的三角函数公式：

• $\sin \left(\frac{A}{2}\right)=\pm \sqrt{\frac{1-\cos (A)}{2}}$
• $\cos \left(\frac{A}{2}\right)=\pm \sqrt{\frac{1+\cos (A)}{2}}$
• $\tan \left(\frac{A}{2}\right)=\pm \sqrt{\frac{1-\cos (A)}{1+\cos (A)}}$

5. 和差化积公式：

• $\sin (A)\sin (B)=\frac{1}{2}[\cos (A-B)-\cos (A+B)]$
• $\cos (A)\cos (B)=\frac{1}{2}[\cos (A-B)+\cos (A+B)]$
• $\sin (A)\cos (B)=\frac{1}{2}[\sin (A-B)+\sin (A+B)]$

6. 和差化积公式的反函数：

• $\sin (A+B)=2\sin \left(\frac{A+B}{2}\right)\cos \left(\frac{A-B}{2}\right)$
• $\sin (A-B)=2\sin \left(\frac{A-B}{2}\right)\cos \left(\frac{A+B}{2}\right)$
• $\cos (A+B)=2\cos \left(\frac{A+B}{2}\right)\cos \left(\frac{A-B}{2}\right)$
• $\cos (A-B)=-2\sin \left(\frac{A+B}{2}\right)\sin \left(\frac{A-B}{2}\right)$

向量

1. 向量加法和减法：

• 加法公式：对于两个向量 $\mathbf{a}(x_1,y_1)$ 和 $\mathbf{b}(x_2,y_2)$，它们的和为 $\mathbf{c}(x_1+x_2,y_1+y_2)$，即 $\mathbf{c}=\mathbf{a}+\mathbf{b}$。
• 减法公式：对于两个向量 $\mathbf{a}(x_1,y_1)$ 和 $\mathbf{b}(x_2,y_2)$，它们的和为 $\mathbf{c}(x_1-x_2,y_1-y_2)$，即 $\mathbf{c}=\mathbf{a}-\mathbf{b}$。

2. 向量数量乘法：

• 数乘公式：对于向量 $\mathbf{a}$ 和标量 $k$，$k$ 乘以向量 $\mathbf{a}$ 的每个分量，即 $k\mathbf{a}$，得到一个新的向量。

3. 点积（内积）：

• 点积公式：对于两个向量 $\mathbf{a}$ 和 $\mathbf{b}$，它们的点积为 $\mathbf{a}\cdot \mathbf{b}=|\mathbf{a}||\mathbf{b}|\cos (\theta )$，其中 $|\mathbf{a}|$ 和 $|\mathbf{b}|$ 分别是向量 $\mathbf{a}$ 和 $\mathbf{b}$ 的模长，$\theta$ 是它们之间的夹角。
• 性质：
  • 对于平行向量，点积为正，$\cos (\theta )=1$。
  • 对于垂直向量，点积为零，$\cos (\theta )=0$。
  • 点积具有交换律：$\mathbf{a}\cdot \mathbf{b}=\mathbf{b}\cdot \mathbf{a}$。
  • 点积具有分配律：$\mathbf{a}\cdot (\mathbf{b}+\mathbf{c})=\mathbf{a}\cdot \mathbf{b}+\mathbf{a}\cdot \mathbf{c}$。
• 用途:

  • 计算夹角：点乘可用于计算两个向量之间的夹角。具体地，两个向量 $\mathbf{a}$ 和 $\mathbf{b}$ 的点乘 $\mathbf{a}\cdot \mathbf{b}$ 等于它们的模长之积与夹角的余弦值的乘积：$\mathbf{a}\cdot \mathbf{b}=|\mathbf{a}||\mathbf{b}|\cos (\theta )$。这可用于判断两个向量的相对方向，例如是否平行、垂直或是在一般的夹角。

  • 投影：点乘可用于计算一个向量在另一个向量上的投影。通过将一个向量 $\mathbf{a}$ 投影到另一个向量 $\mathbf{b}$ 上，可以得到 $\mathbf{a}$ 在 $\mathbf{b}$ 方向上的分量，其大小为 $\mathbf{a}\cdot \mathbf{b}/|\mathbf{b}|$。

  • 工作、能量和功率：点乘在物理学中用于计算力和位移之间的功和能量。力在方向上的分量乘以位移等于所做的功。

4. 叉积（外积）：

• 叉积公式：对于两个三维向量 $\mathbf{a}$ 和 $\mathbf{b}$，它们的叉积 $\mathbf{a}\times \mathbf{b}$ 的计算方式如下：

  $\mathbf{a}\times \mathbf{b}=\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right|$
  其中,ijk分别表示xyz三个轴的基本单位向量，通常我们并不关注。

  这可以通过展开行列式来计算，结果是一个新的向量，其分量为 $c_1$、$c_2$ 和 $c_3$。

• 分量计算：根据行列式展开，$c_1$、$c_2$ 和 $c_3$ 分别计算如下：

  $c_1=a_2{b}_3-a_3{b}_2$
  $c_2=a_3{b}_1-a_1{b}_3$
  $c_3=a_1{b}_2-a_2{b}_1$

• 性质：

  • 叉积的结果是垂直于 $\mathbf{a}$ 和 $\mathbf{b}$ 的向量。
  • 叉积的模长等于 $\mathbf{a}$ 和 $\mathbf{b}$ 构成的平行四边形的面积。
  • 叉积具有反交换律：$\mathbf{a}\times \mathbf{b}=-(\mathbf{b}\times \mathbf{a})$。
  • 叉积具有分配律：$\mathbf{a}\times (\mathbf{b}+\mathbf{c})=\mathbf{a}\times \mathbf{b}+\mathbf{a}\times \mathbf{c}$。

• 作用：

  • 法向量：叉乘可用于计算平面上三个点或三个向量所确定的平面的法向量。对于两个向量 $\mathbf{a}$ 和 $\mathbf{b}$ 的叉乘 $\mathbf{a}\times \mathbf{b}$，结果是一个垂直于 $\mathbf{a}$ 和 $\mathbf{b}$ 平面的向量，其方向遵循右手定则。

  • 面积：叉乘的模长等于两个向量所张成的平行四边形（或平行四边形的面积）的面积。这在计算几何学中非常有用。

  • 角动量和扭矩：在物理学和工程学中，叉乘用于计算角动量和扭矩（力矩）。角动量是物体旋转时的动力学性质，而扭矩用于描述力对物体的旋转作用。

  • 电磁学中的洛伦兹力：在电磁学中，洛伦兹力的计算涉及电荷、电场和磁场之间的叉乘关系。

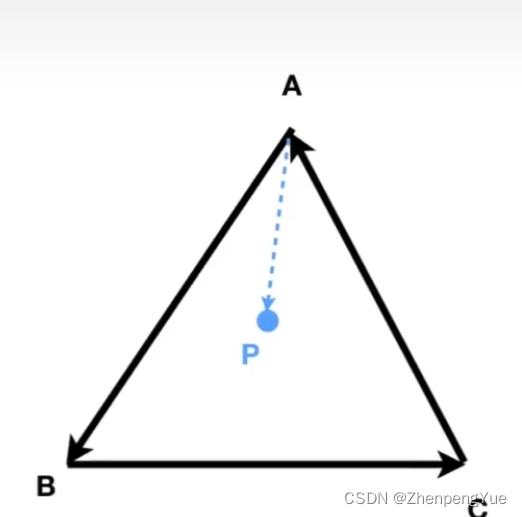
  • 在图形学中判断点是否在三角形内，点在三边左侧(与A/B/C P叉乘)
    

右手定则

a. 伸开你的右手，将大拇指、食指和中指垂直伸出，使它们呈 90 度角。

b. 让大拇指指向第一个输入向量 $\mathbf{a}$ 的方向。

c. 让食指指向第二个输入向量 $\mathbf{b}$ 的方向。

d. 你的中指所指向的方向就是结果法向量 $\mathbf{n}$ 的方向。

e. 方向的确定是根据右手的构型而来，所以它遵循右手定则。

5. 混合积（三重积）：

• 混合积公式：对于三个向量 $\mathbf{a}$、$\mathbf{b}$ 和 $\mathbf{c}$，它们的混合积为 $\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})$。混合积表示了这三个向量所构成的平行六面体的有向体积。
• 性质：
  • 混合积的绝对值等于平行六面体的体积。
  • 混合积可以用来判断三个向量是否共面，如果混合积为零，它们共面。