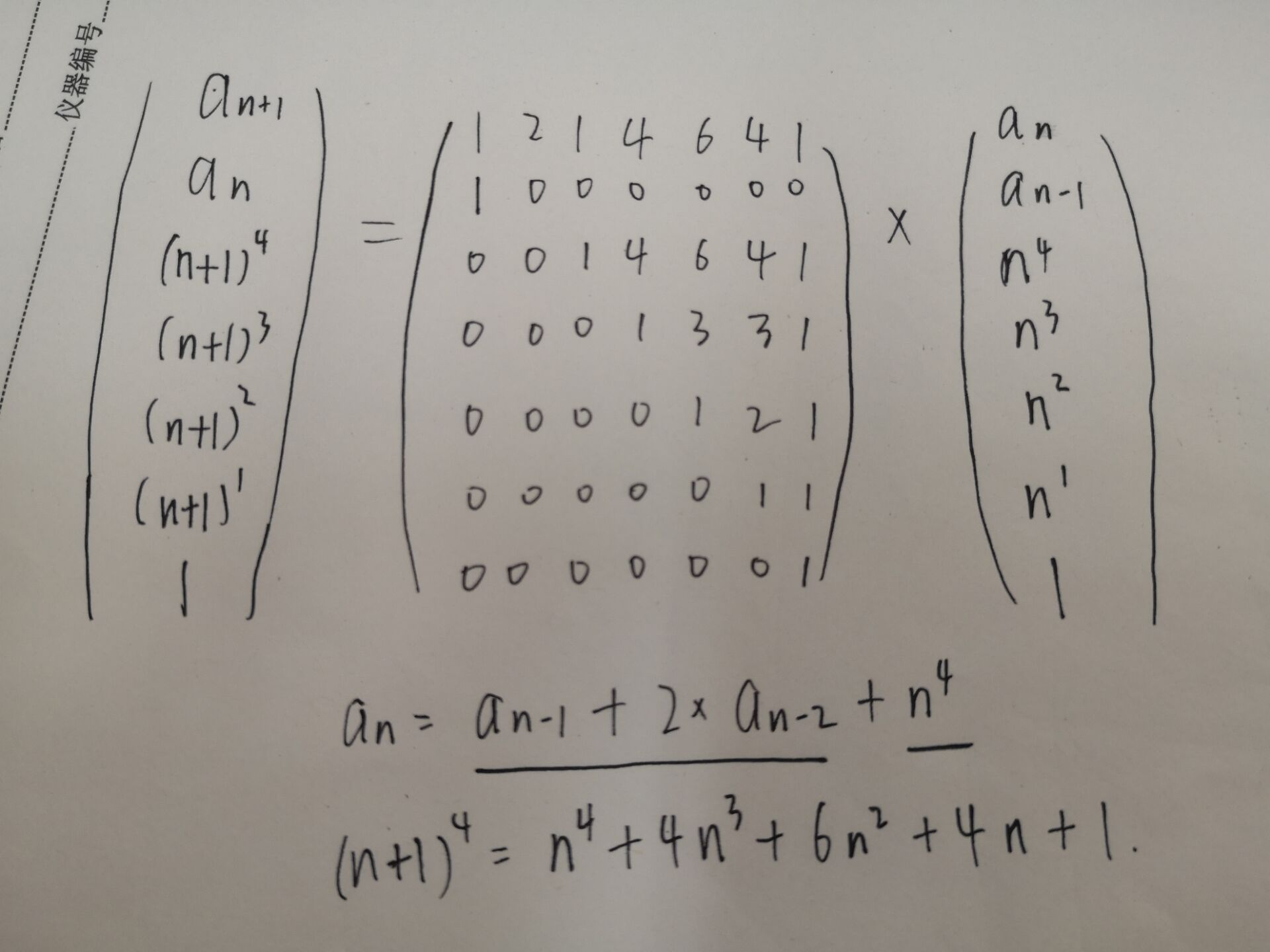HDU - 5950 Recursive sequence（二项式+矩阵合并+矩阵快速幂）

Recursive sequence

 

Farmer John likes to play mathematics games with his N cows. Recently, they are attracted by recursive sequences. In each turn, the cows would stand in a line, while John writes two positive numbers a and b on a blackboard. And then, the cows would say their identity number one by one. The first cow says the first number a and the second says the second number b. After that, the i-th cow says the sum of twice the (i-2)-th number, the (i-1)-th number, and i4i4. Now, you need to write a program to calculate the number of the N-th cow in order to check if John’s cows can make it right. 

InputThe first line of input contains an integer t, the number of test cases. t test cases follow. 
 Each case contains only one line with three numbers N, a and b where N,a,b < 231231 as described above. 
OutputFor each test case, output the number of the N-th cow. This number might be very large, so you need to output it modulo 2147493647.Sample Input

2
3 1 2
4 1 10

Sample Output

85
369

        
 

Hint

In the first case, the third number is 85 = 2*1十2十3^4.
 In the second case, the third number is 93 = 2*1十1*10十3^4 and the fourth number is 369 = 2 * 10 十 93 十 4^4.

矩阵快速幂。利用了矩阵合并将两个递推关系合并到一个矩阵中。
之前做过了不少含有变量项的题，这道题是底数为变量，指数为常数的一种。
其中变量项的递推利用了二项式定理，系数满足杨辉三角规律。

#include <bits/stdc++.h>
#define MAX 10
#define MOD 2147493647
using namespace std;
typedef long long ll;

struct mat{
    ll a[MAX][MAX];
};

mat operator *(mat x,mat y)
{
    mat ans;
    memset(ans.a,0,sizeof(ans.a));
    for(int i=1;i<=7;i++){
        for(int j=1;j<=7;j++){
            for(int k=1;k<=7;k++){
                ans.a[i][j]+=(x.a[i][k]*y.a[k][j]+MOD)%MOD;
                ans.a[i][j]%=MOD;
            }
        }
    }
    return ans;
}
mat qMod(mat a,ll n)
{
    ll tt[][8]={0,0,0,0,0,0,0,0,
                0,1,2,1,4,6,4,1,
                0,1,0,0,0,0,0,0,
                0,0,0,1,4,6,4,1,
                0,0,0,0,1,3,3,1,
                0,0,0,0,0,1,2,1,
                0,0,0,0,0,0,1,1,
                0,0,0,0,0,0,0,1};
    mat t;
    for(int i=1;i<=7;i++){
        for(int j=1;j<=7;j++){
            t.a[i][j]=tt[i][j];
        }
    }
    while(n){
        if(n&1) a=t*a;
        n>>=1;
        t=t*t;
    }
    return a;
}
int main()
{
    int t,i,j;
    ll n,a,b;
    scanf("%d",&t);
    while(t--){
        scanf("%I64d%I64d%I64d",&n,&a,&b);
        if(n<3){
            if(n==1) printf("%I64d\n",a);
            if(n==2) printf("%I64d\n",b);
            continue;
        }
        mat x;
        memset(x.a,0,sizeof(x.a));
        x.a[1][1]=b;
        x.a[2][1]=a;
        x.a[3][1]=2*2*2*2;
        x.a[4][1]=2*2*2;
        x.a[5][1]=2*2;
        x.a[6][1]=2;
        x.a[7][1]=1;
        x=qMod(x,n-2);
        printf("%I64d\n",x.a[1][1]);
    }
    return 0;
}