第一周:深度学习基础
第一周:深度学习基础
经过了第一周的学习,对深度学习有了系统的认识。
- 视频学习
- 1.1 绪论
- 1.2 深度学习概述
- 1.3 pytorch基础
- 代码练习
- 2.1 螺旋数据分类
- 2.2 回归分析
1. 视频学习
通过视频学习整理出以下知识点,做好理论储备。
1.1 绪论
AI诞生:1956年美国达特茅斯会议:人工智能 (Artificial Intelligence) 概念诞生。
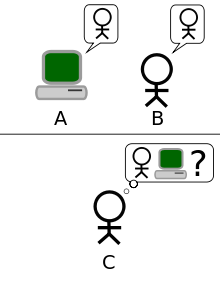
图灵测试(英语:Turing test,又译图灵试验)是图灵于1950年提出的一个关于判断机器是否能够思考的著名思想实验,测试某机器是否能表现出与人等价或无法区分的智能。测试的谈话仅限于使用唯一的文本管道,例如计算机键盘和屏幕,这样的结果不依赖于计算机把单词转换为音频的能力。
——维基百科
关系:人工智能>机器学习>深度学习

机器学习应用领域:
计算机视觉(CV)、语音识别、自然语言处理(NLP)
计算机视觉应用:图像分类、目标检测、语义分割等
机器学习三要素:
- 模型:问题建模、确定假设空间
- 策略:确定目标函数
- 算法:求解模型参数
对于模型的分类:
- 数据标记:监督学习模型、无监督学习模型(半监督学习模型、强化学习模型)
- 数据分布:参数模型、非参数模型
- 建模对象:判别模型、生成模型
知识工程(专家系统) vs 机器学习(神经网络)
知识图谱(符号主义) vs 深度学习(连接主义)

机器学习模型:

人工智能的发展:
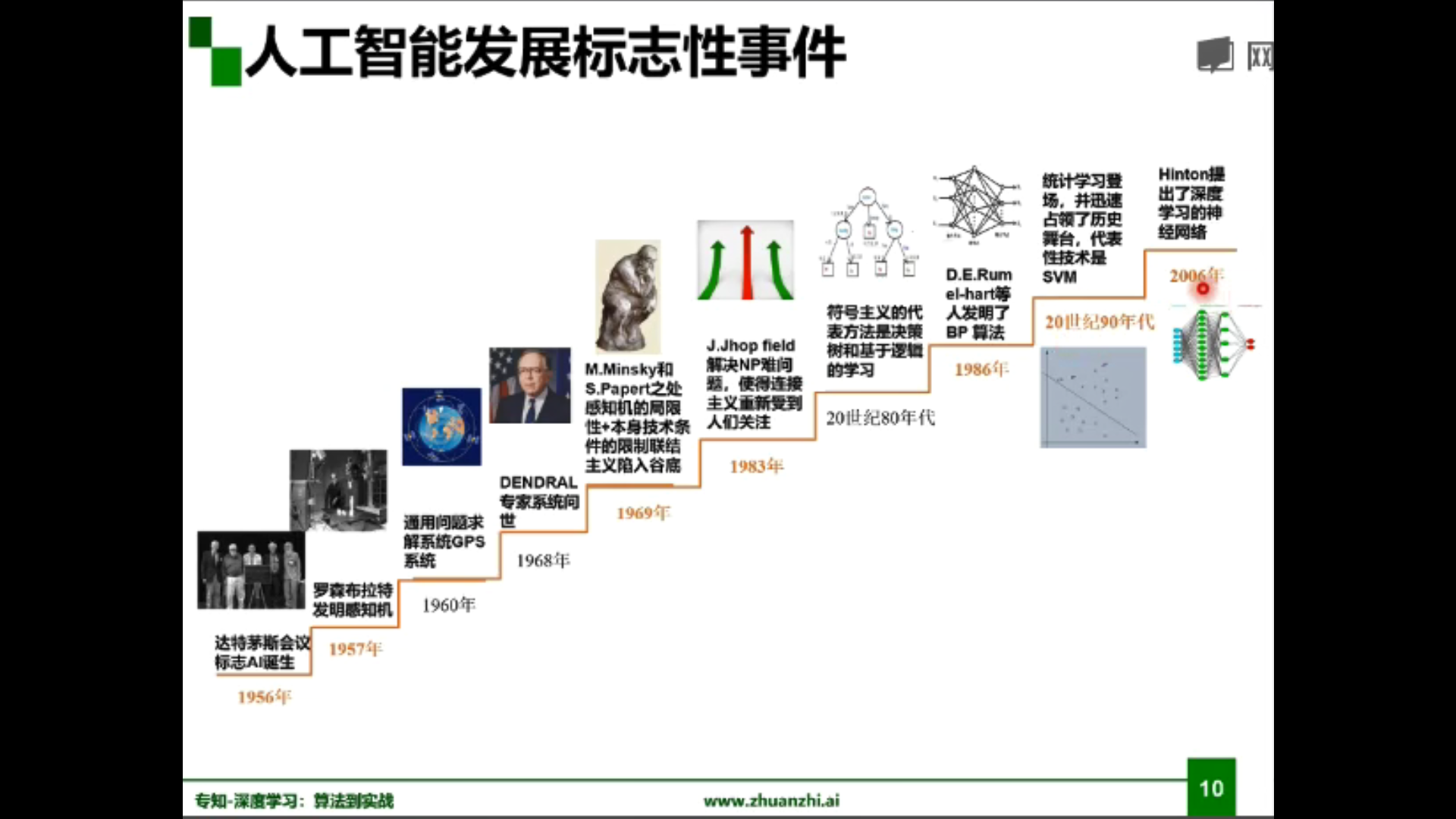
标志性人物:
| 名称 | 事件 |
|---|---|
| Rosenblatt | 提出感知机(Perceptron) |
| Minsky | 论证了感知机的局限(异或门与计算量) |
| Rumelhart | 阐述BP反向传播算法及其应用 |
| Yann Lecun | 运用卷积神经网络(CNN) |
| Geoffrey Hinton | 坚守神经网络研究,并改名深度学习(Deep Learning),发表深度置信网络(DBN)并使用限制玻尔兹曼机(RBM)学习 |
| Andrew Ng | 使用GPU加快运行速度 |
| 李飞飞 | 宣布建立超大型图像数据库ImageNet,ILSVRC竞赛成为技术突破的转折点 |
| Yoshua Bengio | 使用修正线性单元(ReLU)作为激励函数 |
| Schmidhuber | 提出了长短期记忆(LSTM)的计算模型 |
| Ian Goodfellow | 提出生成式对抗网络(GANs) |
2019年图灵奖:Geoffrey Hinton, Yann LeCun,和Yoshua Bengio
1.2 深度学习概述
神经网络结构的发展:
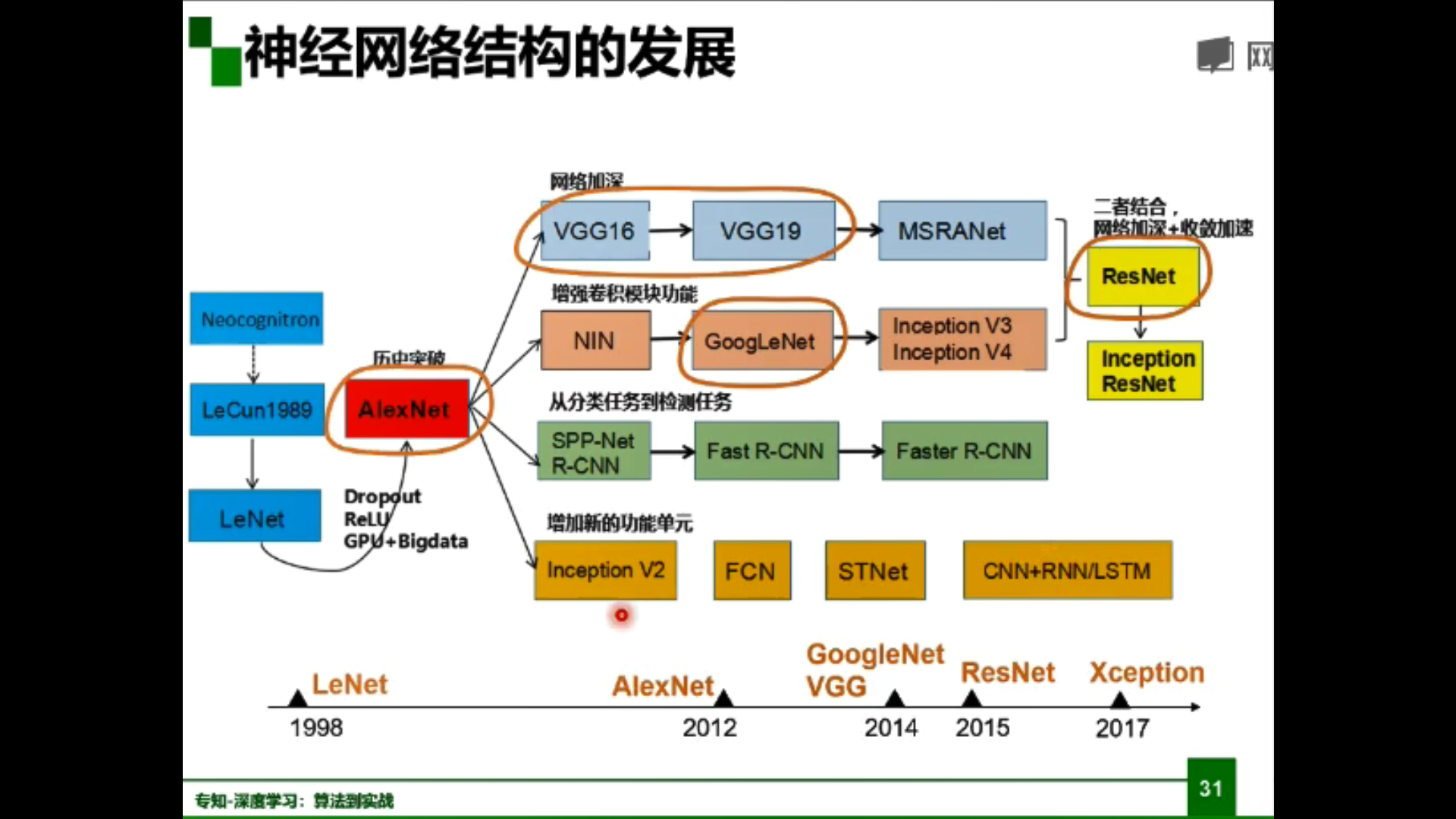
深度学习三个助推剂:大数据、算法、计算力
深度学习的局限性:
线性回归、决策树、SVM、随机森林、深度学习,从左往右准确性(泛化性)递增,解释性递减。

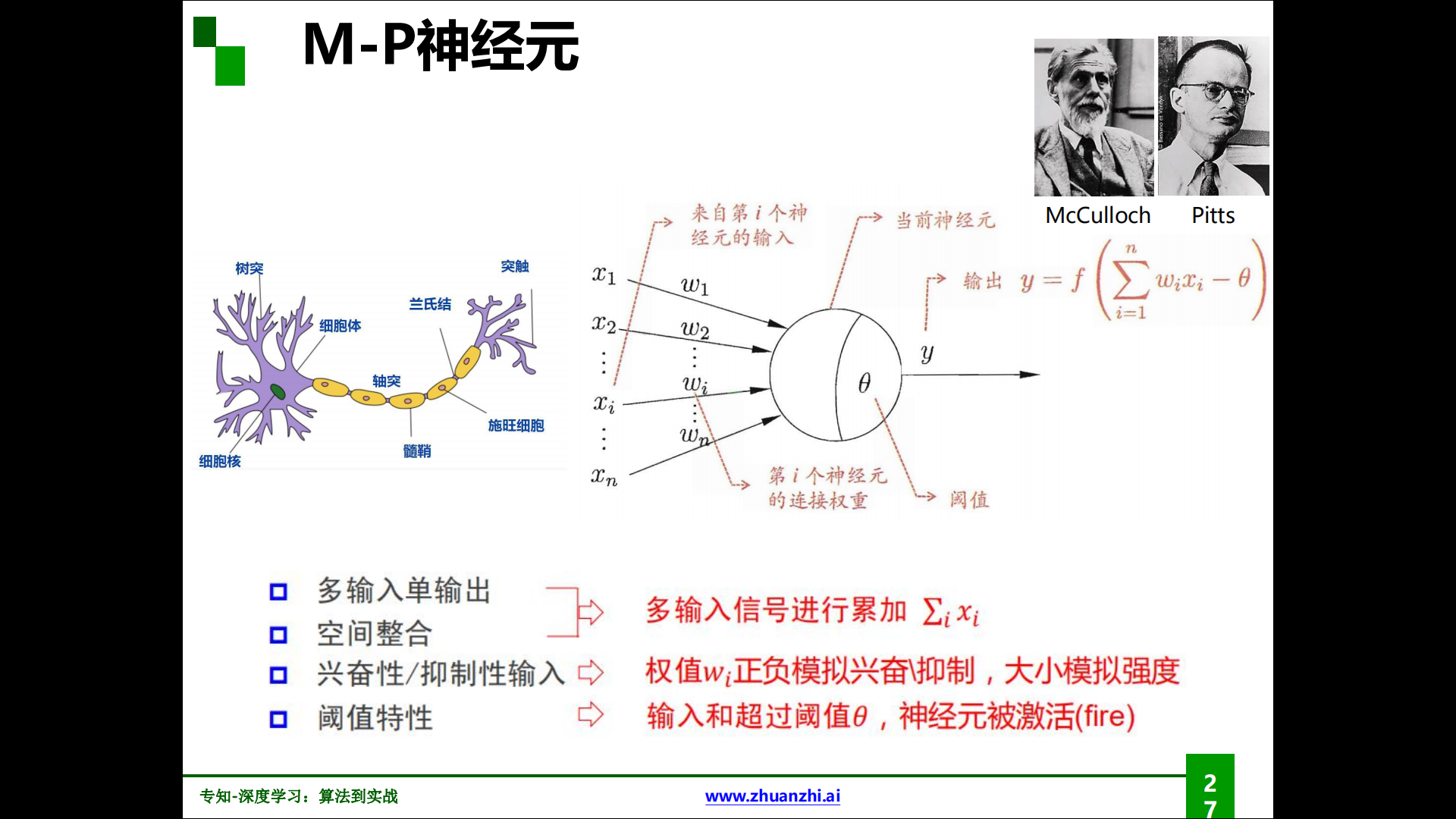
M-P神经元:
M-P神经元由McCulloch与Pitts发现并命名,作为神经网络的基本单位。
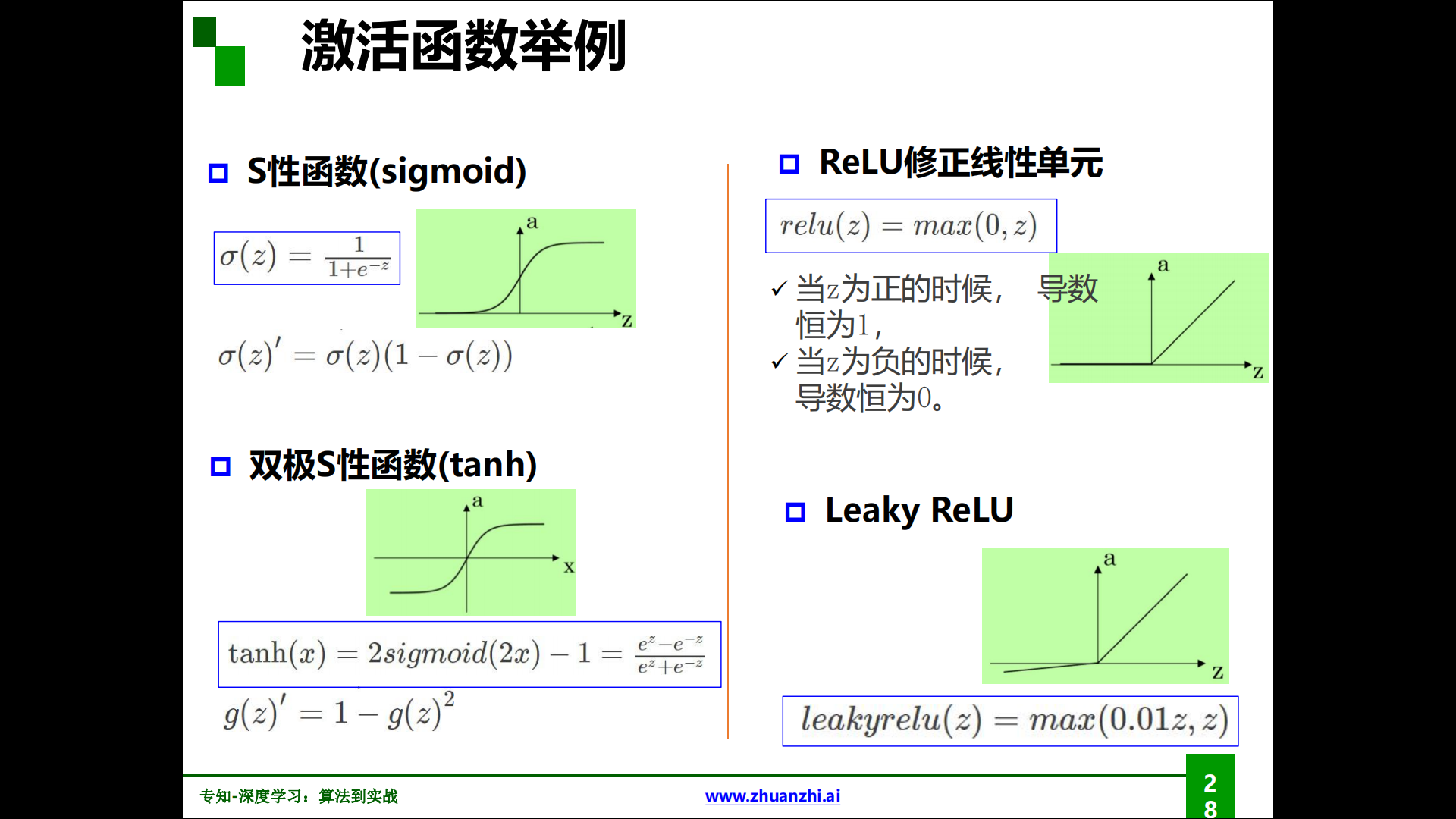
各种激活函数:
万有逼近定理:
- 如果一个隐层包含足够多的神经元,三层前馈神经网络(输入-隐层-输出)能以任意精度逼近任意预定的连续函数。
- 当隐层足够宽时,双隐层感知器(输入-隐层1-隐层2-输出)可以逼近任意非连续函数:可以解决任何复杂的分类问题。
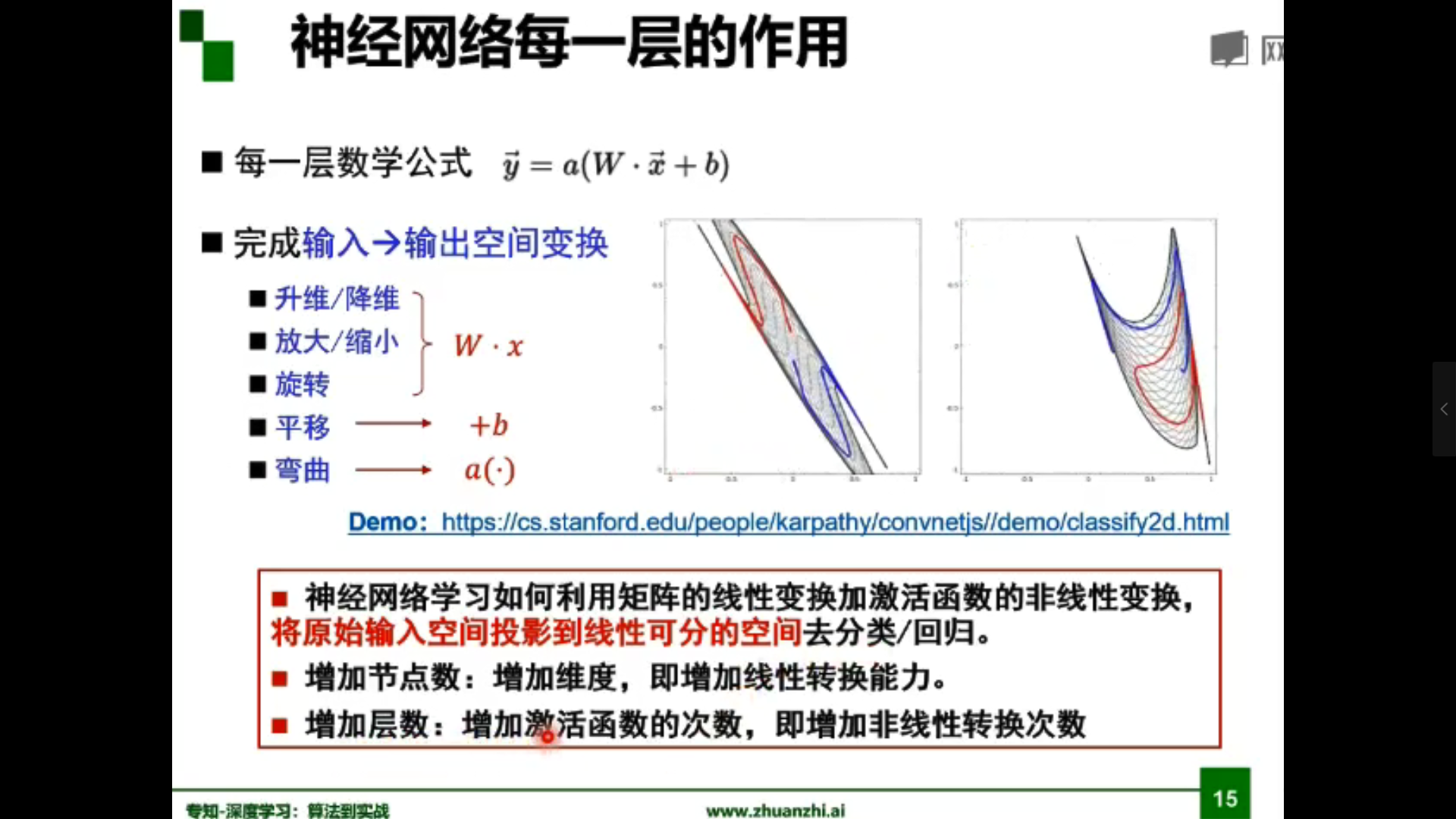
为什么线性分类任务组合后可以解决非线性分类任务?
答:第一层感知器经过空间变换将非线性问题转化为线性问题。
| 结构 | 决策区域类型 |
|---|---|
| 无隐层 | 由一超平面分成两个 |
| 单隐层 | 开凸区域或闭凸区域 |
| 双隐层 | 任意形状(复杂度由单元数目确定) |
-
梯度:一个向量。方向是最大方向导数的方向。模为方向导数的最大值。
-
梯度下降:参数沿负梯度方向更新可以使函数值下降。
-
反向传播:根据损失函数计算的误差通过反向传播的方式,指导深度网络参数的更新优化。
为什么使用梯度下降来优化神经网络参数?
我们的目的是让损失函数取得极小值。所以就变成了一个寻找函数最小值的问题,在数学上,很自然的就会想到使用梯度下降来解决。
深度学习两个优化器:Adam、SGD(随机梯度下降)
一般Adam效果较好。
梯度消失、爆炸会带来哪些影响?
举个例子,对于一个含有三层隐藏层的简单神经网络来说,当梯度消失发生时,接近于输出层的隐藏层由于其梯度相对正常,所以权值更新时也就相对正常,但是当越靠近输入层时,由于梯度消失现象,会导致靠近输入层的隐藏层权值更新缓慢或者更新停滞。这就导致在训练时,只等价于后面几层的浅层网络的学习。
神经网络的第三次兴起:
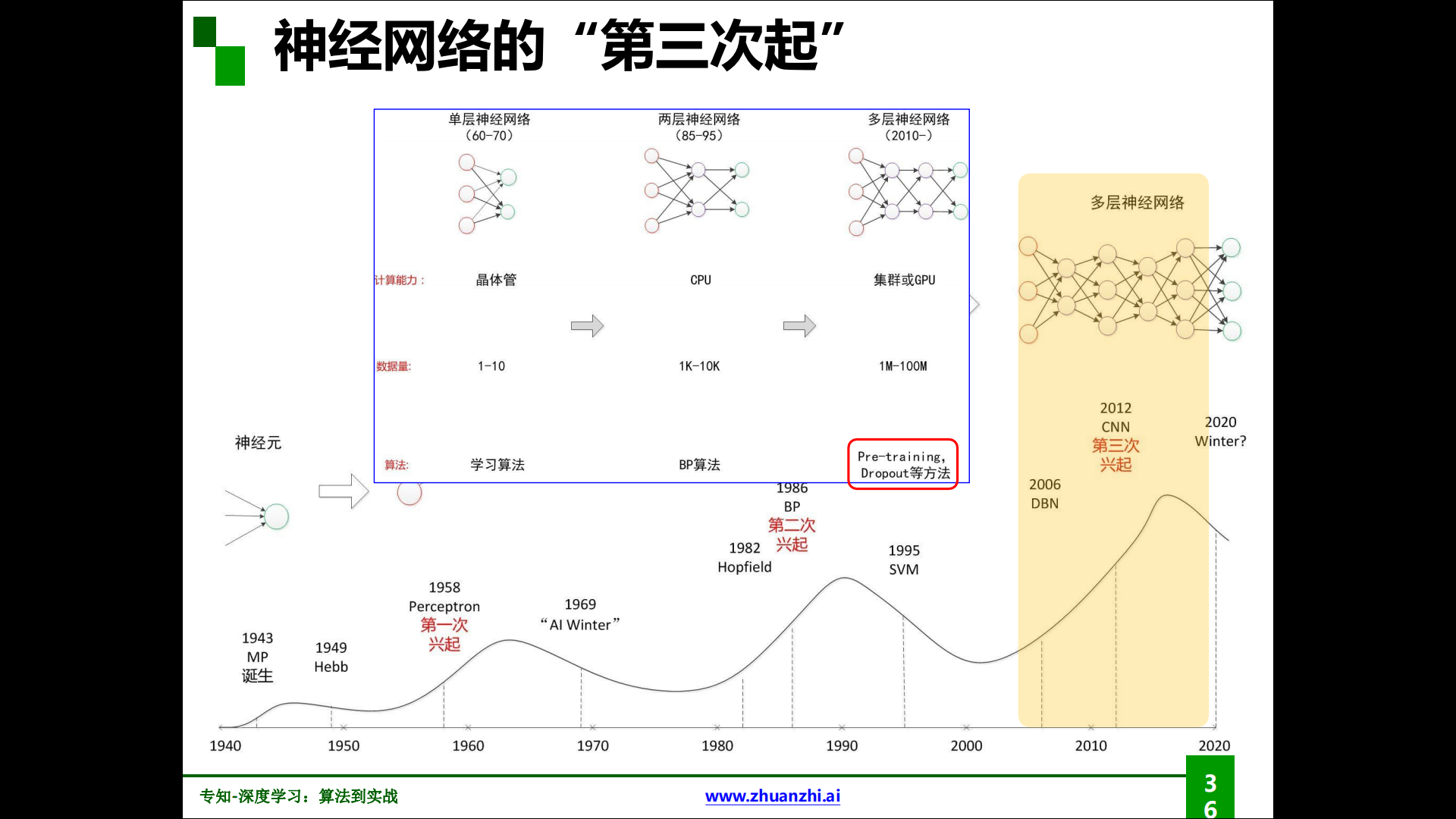
解决梯度消失的方法:

逐层预训练(layer-wise pre-training):权重初始化,拥有一个较好的初始值,尽可能避免局部极小值梯度消失。
- 受限玻尔兹曼机(RBM)
- 自编码器(Autoencoder)
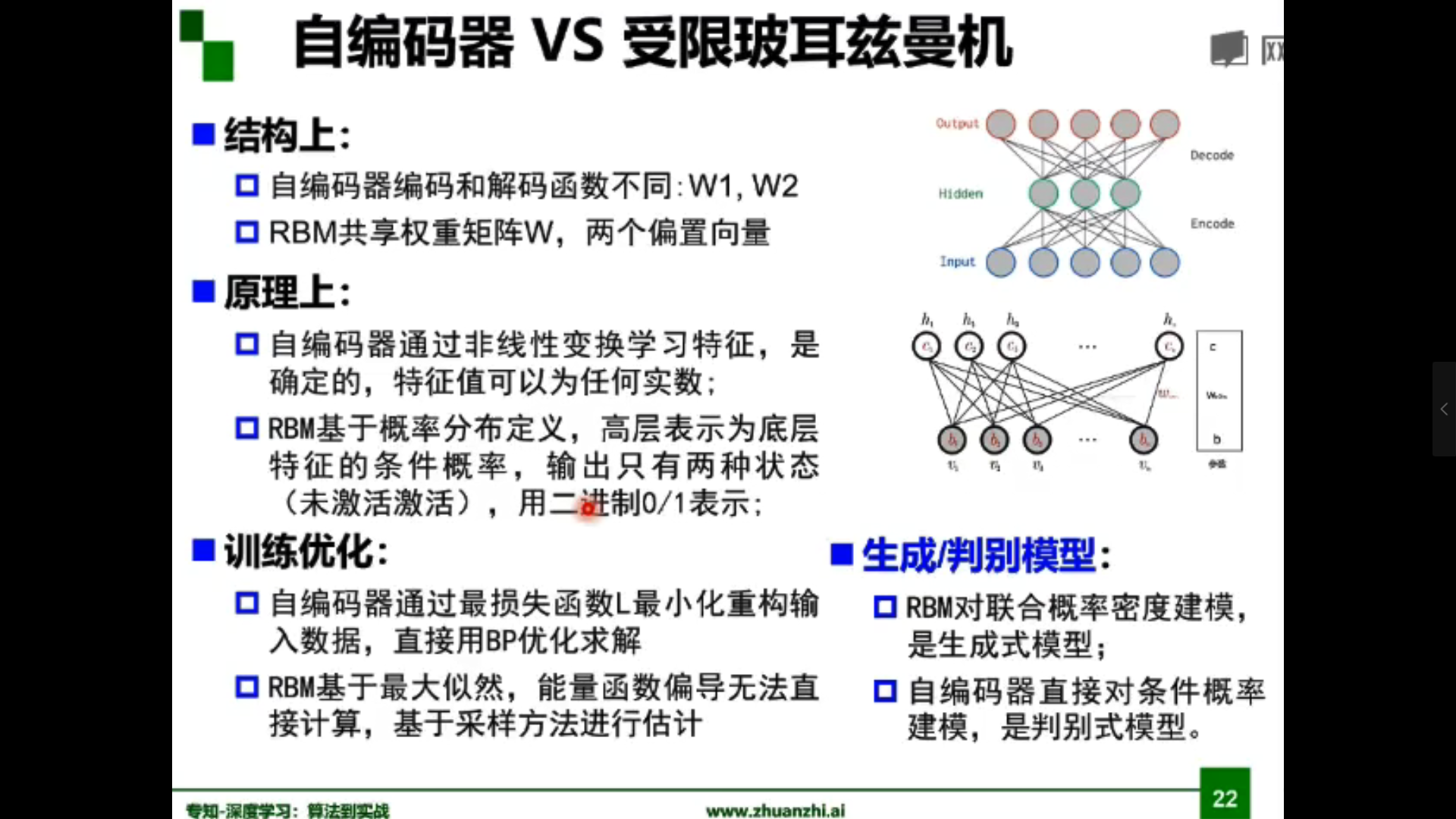
自编码器原理:
假设输出与输入相同(target=input),是一种尽可能复现输入信号的神经网络。通过调整encoder和decoder的参数,使得重构误差最小。
自编码器可实现降维、去噪

微调(fine-tune)
1.3 pytorch基础
- torch.Tensor(张量,各种类型数据的封装)
- data属性,用来存数据
- grad属性,用来存梯度
- grad_fn,用来指向创造自己的Function
- torch.autograd.Function(函数类,定义在Tensor类上的操作)
如何用Pytorch完成实验?
- 加载、预处理数据集
- 构建模型
- 定义损失函数
- 实现优化算法
- 迭代训练
- 加速计算(GPU)
- 存储模型
- 构建baseline
2. 代码练习
理论指导实践,这里引入中国海洋大学视觉实验室前沿理论小组 pytorch 学习中03分类问题(离散性)、04回归问题(连续性)两个经典的范例,通过Colaboratory运行代码观察结果,并写下一点自己的理解。
在训练模型时,如果训练数据过多,无法一次性将所有数据送入计算,那么我们就会遇到epoch,batchsize,iterations这些概念。为了克服数据量多的问题,我们会选择将数据分成几个部分,即batch,进行训练,从而使得每个批次的数据量是可以负载的。将这些batch的数据逐一送入计算训练,更新神经网络的权值,使得网络收敛。
一个epoch指代所有的数据送入网络中完成一次前向计算及反向传播的过程。
所谓Batch就是每次送入网络中训练的一部分数据,而Batch Size就是每个batch中训练样本的数量
iterations就是完成一次epoch所需的batch个数。
问题:
- 神经网络的输出层需要激活函数吗?
2.1 螺旋数据分类
这里有三点需要注意:
每一次反向传播前,都要把梯度清零:当GPU显存较少时,又想要调大batch-size,此时就可以利用PyTorch默认进行梯度累加的性质来进行backward。
梯度累加就是,每次获取1个batch的数据,计算1次梯度,梯度不清空,不断累加,累加一定次数后,根据累加的梯度更新网络参数,然后清空梯度,进行下一次循环。
一定条件下,batchsize越大训练效果越好,梯度累加则实现了batchsize的变相扩大,如果accumulation_steps为8,则batchsize '变相' 扩大了8倍,是我们这种乞丐实验室解决显存受限的一个不错的trick,使用时需要注意,学习率也要适当放大。
——知乎Pascal
加入ReLU激活函数,分类的准确率显著提高:非线性变换。
为什么激活函数是非线性的?如果不用激励函数(相当于激励函数是f(x)=x),在这种情况下,每一层的输出都是上一层的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这与一个隐藏层的效果相当(这种情况就是多层感知机MPL)。但当我们需要进行深度神经网络训练(多个隐藏层)的时候,如果激活函数仍然使用线性的,多层的隐藏函数与一层的隐藏函数作用的相当的,就失去了深度神经网络的意义,所以引入非线性函数作为激活函数。
一般在描述神经网络层数时不包括输入层。

2.1.1 构建线性模型分类
learning_rate = 1e-3
lambda_l2 = 1e-5
# nn 包用来创建线性模型
# 每一个线性模型都包含 weight 和 bias
model = nn.Sequential(
nn.Linear(D, H),
nn.Linear(H, C)
)
model.to(device) # 把模型放到GPU上
# nn 包含多种不同的损失函数,这里使用的是交叉熵(cross entropy loss)损失函数
criterion = torch.nn.CrossEntropyLoss()
# 这里使用 optim 包进行随机梯度下降(stochastic gradient descent)优化
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2)
# 开始训练
for t in range(1000):
# 把数据输入模型,得到预测结果
y_pred = model(X)
# 计算损失和准确率
loss = criterion(y_pred, Y)
score, predicted = torch.max(y_pred, 1)
acc = (Y == predicted).sum().float() / len(Y)
print('[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f' % (t, loss.item(), acc))
display.clear_output(wait=True)
# 反向传播前把梯度置 0
optimizer.zero_grad()
# 反向传播优化
loss.backward()
# 更新全部参数
optimizer.step()
[EPOCH]: 999, [LOSS]: 0.861541, [ACCURACY]: 0.504
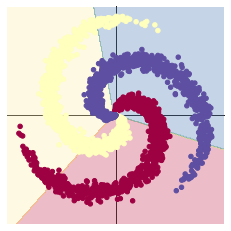
2.1.2 构建两层神经网络分类
learning_rate = 1e-3
lambda_l2 = 1e-5
# 这里可以看到,和上面模型不同的是,在两层之间加入了一个 ReLU 激活函数
model = nn.Sequential(
nn.Linear(D, H),
nn.ReLU(),
nn.Linear(H, C)
)
model.to(device)
# 下面的代码和之前是完全一样的,这里不过多叙述
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=lambda_l2) # built-in L2
# 训练模型,和之前的代码是完全一样的
for t in range(1000):
y_pred = model(X)
loss = criterion(y_pred, Y)
score, predicted = torch.max(y_pred, 1)
acc = ((Y == predicted).sum().float() / len(Y))
print("[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f" % (t, loss.item(), acc))
display.clear_output(wait=True)
# zero the gradients before running the backward pass.
optimizer.zero_grad()
# Backward pass to compute the gradient
loss.backward()
# Update params
optimizer.step()
[EPOCH]: 999, [LOSS]: 0.183681, [ACCURACY]: 0.943
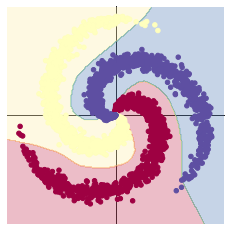
2.2 回归分析
两点思考:
对比三类激活函数:
| 函数 | 优点 | 缺点 |
|---|---|---|
| Sigmoid | Sigmoid函数是深度学习领域开始时使用频率最高的激活函数,它是便于求导的平滑函数,能够将输出值压缩到0-1范围之内 | 容易出现梯度消失;输出不是zero-centered;幂运算相对耗时 |
| Tanh | 全程可导;输出区间为-1到1;解决了zero-centered的输出问题 | 梯度消失的问题和幂运算的问题仍然存在 |
| ReLU | 解决了梯度消失的问题 (在正区间);计算速度非常快,只需要判断输入是否大于0;收敛速度远快于Sigmoid和Tanh;ReLU会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生 | 输出不是zero-centered;某些神经元可能永远不会被激活,导致相应的参数永远不能被更新(Dead ReLU Problem) |
有两个主要原因可能导致Dead ReLU Problem:
- 非常不幸的参数初始化,这种情况比较少见
- 学习速率太高导致在训练过程中参数更新太大,不幸使网络进入这种状态
解决方法:可以采用Xavier初始化方法,以及避免将学习速率设置太大或使用adagrad等自动调节学习速率的算法。
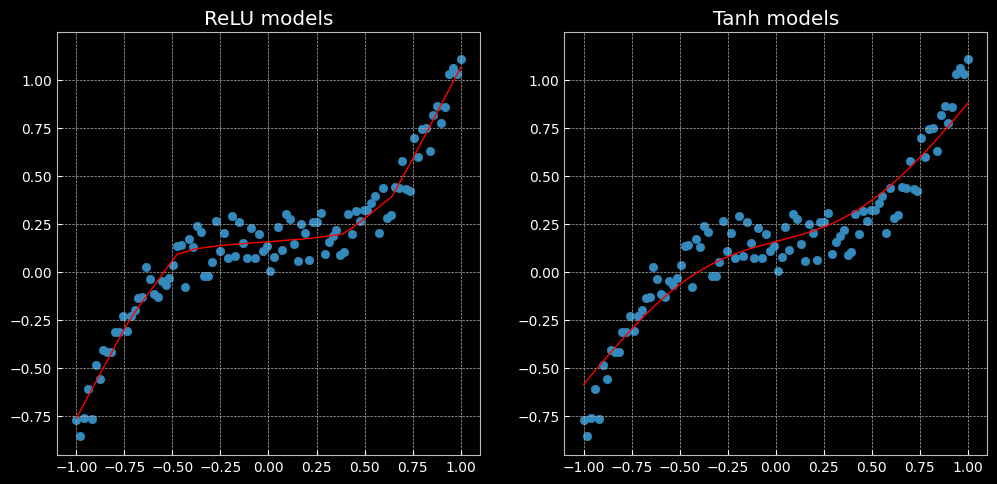
ReLU与Tanh表现效果不同:前者是分段的线性函数,而后者是连续且平滑的回归。
The former is a piecewise linear function, whereas the latter is a continuous and smooth regression.
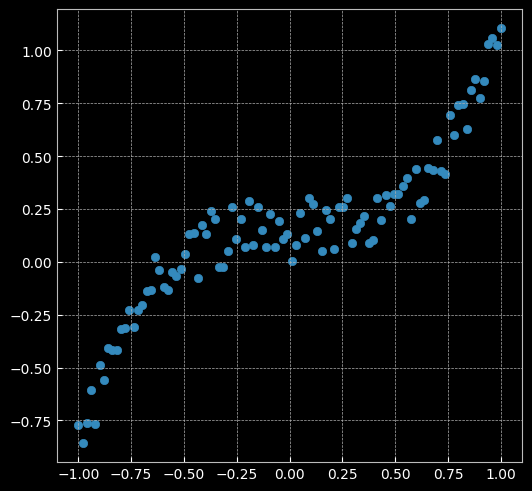
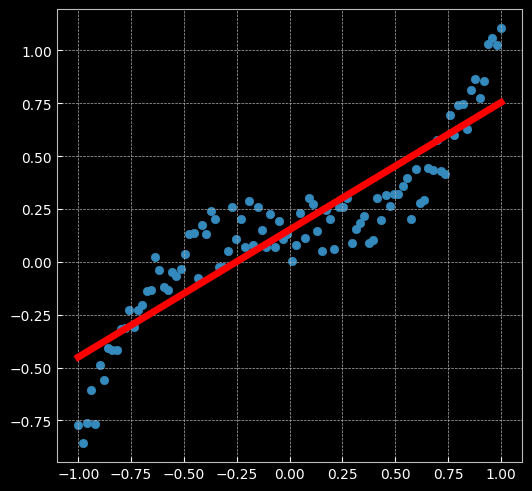
2.2.1 建立线性模型(两层网络间没有激活函数)
learning_rate = 1e-3
lambda_l2 = 1e-5
# 建立神经网络模型
model = nn.Sequential(
nn.Linear(D, H),
nn.Linear(H, C)
)
model.to(device) # 模型转到 GPU
# 对于回归问题,使用MSE损失函数
criterion = torch.nn.MSELoss()
# 定义优化器,使用SGD
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2) # built-in L2
# 开始训练
for t in range(1000):
# 数据输入模型得到预测结果
y_pred = model(X)
# 计算 MSE 损失
loss = criterion(y_pred, y)
print("[EPOCH]: %i, [LOSS or MSE]: %.6f" % (t, loss.item()))
display.clear_output(wait=True)
# 反向传播前,梯度清零
optimizer.zero_grad()
# 反向传播
loss.backward()
# 更新参数
optimizer.step()
[EPOCH]: 999, [LOSS or MSE]: 0.029701
2.2.2 两层神经网络
# 这里定义了2个网络,一个 relu_model,一个 tanh_model,
# 使用了不同的激活函数
relu_model = nn.Sequential(
nn.Linear(D, H),
nn.ReLU(),
nn.Linear(H, C)
)
relu_model.to(device)
tanh_model = nn.Sequential(
nn.Linear(D, H),
nn.Tanh(),
nn.Linear(H, C)
)
tanh_model.to(device)
# MSE损失函数
criterion = torch.nn.MSELoss()
# 定义优化器,使用 Adam,这里仍使用 SGD 优化器的化效果会比较差,具体原因请自行百度
optimizer_relumodel = torch.optim.Adam(relu_model.parameters(), lr=learning_rate, weight_decay=lambda_l2)
optimizer_tanhmodel = torch.optim.Adam(tanh_model.parameters(), lr=learning_rate, weight_decay=lambda_l2)
# 开始训练
for t in range(1000):
y_pred_relumodel = relu_model(X)
y_pred_tanhmodel = tanh_model(X)
# 计算损失与准确率
loss_relumodel = criterion(y_pred_relumodel, y)
loss_tanhmodel = criterion(y_pred_tanhmodel, y)
print(f"[MODEL]: relu_model, [EPOCH]: {t}, [LOSS]: {loss_relumodel.item():.6f}")
print(f"[MODEL]: tanh_model, [EPOCH]: {t}, [LOSS]: {loss_tanhmodel.item():.6f}")
display.clear_output(wait=True)
optimizer_relumodel.zero_grad()
optimizer_tanhmodel.zero_grad()
loss_relumodel.backward()
loss_tanhmodel.backward()
optimizer_relumodel.step()
optimizer_tanhmodel.step()
[MODEL]: relu_model, [EPOCH]: 999, [LOSS]: 0.006584
[MODEL]: tanh_model, [EPOCH]: 999, [LOSS]: 0.014194