省选训练做题笔记 ~~Belive You Can~~
不太会取标题。但是 \(\text{Belive}\neq \text{Believe}\)。
Hammer to Fall
考虑倒着 DP 出每个点每个人需要多少代价才能安全。每一次只会对 \(b_i\) 修改,你需要遍历 \(b_i\) 这个点的邻域。
图邻域让我们联想到根号分治,我们可以用 set 维护出所有度数大于根号的点的即将更新出的 DP 值。复杂度 \(O(q\sqrt {m\log m})\)。
这虽然能过,但是带了 \(\log\),好逊啊。考虑对于时间序列分块,那么对于每个点求出按当前 DP 值更新这个点的代价前 \(B+1\) 大。由于当前时间块中最多只会修改 \(B\) 个,当这个点被更新时它一定可以在这些点中取到最优值。复杂度 \(O(q\sqrt m)\)。
#include <cmath>
#include <cstdio>
#include <vector>
#include <algorithm>
#define fi first
#define se second
using namespace std;
int read(){
char c=getchar();int x=0;
while(c<48||c>57) c=getchar();
do x=(x<<1)+(x<<3)+(c^48),c=getchar();
while(c>=48&&c<=57);
return x;
}
typedef long long ll;
const int N=100003,P=998244353;
const ll INF=0x3f3f3f3f3f3f3f3f;
typedef pair<int,int> pii;
vector<pii> vec[N];
int n,m,q,sq;
int a[N],b[N];
ll f[N];
int main(){
n=read();m=read();q=read();
for(int i=1;i<=n;++i) a[i]=read();
for(int i=1;i<=m;++i){
int u=read(),v=read(),w=read();
vec[u].emplace_back(v,w);
vec[v].emplace_back(u,w);
}
for(int i=1;i<=q;++i) b[i]=read();
sq=ceil(sqrt(m));
for(int r=q;r>0;r-=sq){
for(int i=1;i<=n;++i)
if(int(vec[i].size())>sq)
nth_element(vec[i].begin(),vec[i].begin()+sq,vec[i].end(),[](pii x,pii y){return f[x.fi]+x.se<f[y.fi]+y.se;});
for(int i=r;i>r-sq&&i;--i){
int x=b[i],tmp=0;
f[x]=INF;
for(pii cur:vec[x]){
if(f[x]>f[cur.fi]+cur.se) f[x]=f[cur.fi]+cur.se;
if(++tmp>sq) break;
}
}
}
int res=0;
for(int i=1;i<=n;++i) res=(res+f[i]%P*a[i])%P;
printf("%d\n",res);
return 0;
}
神隐
如何确定边 \((i,j)\) 是否在原图中呢?我们发现对于原图中的点对,它们之间是否联通完全取决于中间这条边有没有神隐。于是我们考虑对每条边安排它在哪些试验中出现,设为 \(msk_i\)。如果 \((i,j)\) 之间有连边,那么它们之间的联通状态就是 \(msk_{(i,j)}\),否则是 \(\cap_{e\in path(i,j)} msk_e\)。如何安排每次试验使得它能直接区分出每条边呢?考虑 gc 学姐曾经讲过的某道题的套路,我们只取 \(\text{popcount}=\frac{limit}{2}\) 的状态。这样任意两个状态的交都比 \(\frac{limit}{2}\) 小了。
于是我们得到了一个 \(O(n^2limit)\) 的做法,暴力枚举点对然后看一下它们之间在同一个连通块的次数是不是 \(\frac{limit}{2}\)。
接下来只要考虑优化重建树的过程就行了。我们要多多利用树的性质。对于树上交互题我们常见的想法是剥叶子。
容易发现这道题中剥叶子是好办的。我们只需要找到哪些点作为一个联通块单独出现的次数恰好是一半就行了。于是我们相当于可以给这棵树定一个深度一样的东西。
有了这个东西,我们再考虑一下对于你询问的方式,任意两条边一定存在一个询问满足一条边问了的同时另一条边没有。所以说你强制让连向一条叶子边问了而连向父亲的边没问,此时该连通块中深度最小的点就是连向叶子的点了。复杂度 \(O(nlimit^2)\)
#include "tree.h"
#include <algorithm>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/hash_policy.hpp>
using namespace std;
typedef vector<int> vi;
typedef vector<vi> vvi;
typedef pair<int,int> pii;
typedef __gnu_pbds::gp_hash_table<int,bool> ump;
vector<pii> solve(int n){
int m=10;
if(n<=2000) m=7;
int mm=m<<1;
int cur=(1<<m)-1;
vector<int> msk(n-1);
for(int i=0;i<n-1;++i){
msk[i]=cur;
int lb=cur&-cur,r=cur+lb;
cur=((r^cur)>>__builtin_ctz(lb)+2)|r;
}
vvi col(mm,vi(n)),sz(mm),id(mm);
vector<vvi> con(mm);
vi que(n),buc(n),p(n);int tl=0;
for(int x=0;x<mm;++x){
vi qv(n-1);
for(int i=0;i<n-1;++i) qv[i]=msk[i]>>x&1;
con[x]=query(qv);
int cnt=0;
sz[x].resize(con[x].size());
id[x].resize(con[x].size(),0);
for(vi tmp:con[x]){
sz[x][cnt]=tmp.size();
for(int i:tmp) id[x][col[x][i]=cnt]^=i;
if(sz[x][cnt]==1){
if(++buc[id[x][cnt]]==m) que[tl++]=id[x][cnt];
}
++cnt;
}
}
for(int pos=0;pos<tl;++pos){
int x=que[pos];
for(int i=0;i<mm;++i){
int p=col[i][x];
id[i][p]^=x;
if(--sz[i][p]==1){
if(++buc[id[i][p]]==m) que[tl++]=id[i][p];
}
}
p[x]=pos;
}
vector<pii> res;
vector<ump> vis(n);
auto check=[&](int u,int v)->bool{
if(vis[u].find(v)!=vis[u].end()) return 0;
vis[u][v]=1;
int cnt=0;
for(int x=0;x<mm;++x) if(col[x][u]!=col[x][v]) ++cnt;
return cnt==m;
};
for(int x=0;x<mm;++x){
for(vi tmp:con[x]){
int mx=*max_element(tmp.begin(),tmp.end(),[&](int x,int y)->bool{return p[x]<p[y];});
for(int i:tmp) if(i!=mx&&check(i,mx)) res.emplace_back(i,mx);
}
}
return res;
}
Proposition Composition
hehezhou 似乎讲了一个跟 WD 与地图很像的做法,但是我忘了 qwq。
那就写正常做法,这个题本质是让我们做等价类分裂。链边被非链边覆盖的集合相同的会被分在同一个等价类。
考虑强行维护,你会发现一条边会断开一个等价类当且仅当一个等价类有点在区间里有点在区间外。于是你对区间里的所有点求出最小前驱与最大后继就可以找到需要分裂集合。
分裂集合懒得想了,上了平衡树维护,结果跑得挺快。复杂度是在线的 \(O(n\log n)\)。
#include <cstdio>
#include <random>
#include <algorithm>
#define ls (p<<1)
#define rs (p<<1|1)
#pragma GCC optimize(2,3,"Ofast")
using namespace std;
int read(){
char c=getchar();int x=0;
while(c<48||c>57) c=getchar();
do x=(x<<1)+(x<<3)+(c^48),c=getchar();
while(c>=48&&c<=57);
return x;
}
const int N=250003;
mt19937 rng(random_device{}());
typedef long long ll;
int n,m;
int cnt[N],f[N];
int pre[N],suf[N];
int lc[N],rc[N],sz[N],ft[N];
unsigned long pr[N];
int merge(int x,int y){
if(!x||!y) return x|y;
if(pr[x]<pr[y]){
ft[rc[x]=merge(rc[x],y)]=x;
sz[x]=sz[lc[x]]+sz[rc[x]]+1;
return x;
}
else{
ft[lc[y]=merge(x,lc[y])]=y;
sz[y]=sz[lc[y]]+sz[rc[y]]+1;
return y;
}
}
void split(int p,int k,int &x,int &y){
if(!p){x=y=0;return;}
if(p<=k){x=p;split(rc[p],k,rc[x],y);}
else{y=p;split(lc[p],k,x,lc[y]);}
sz[p]=sz[lc[p]]+sz[rc[p]]+1;
if(lc[p]) ft[lc[p]]=p;
if(rc[p]) ft[rc[p]]=p;
}
inline int jump(int x){while(ft[x]) x=ft[x];return x;}
int rt(int x){
if(f[x]==x) return f[x];
return f[x]=rt(f[x]);
}
int mn[N<<2],mx[N<<2];
void build(int p=1,int l=1,int r=n-1){
if(l==r){mn[p]=pre[l];mx[p]=suf[r];return;}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
mn[p]=min(mn[ls],mn[rs]);
mx[p]=max(mx[ls],mx[rs]);
}
int jumpl(int lim,int bord,int p=1,int l=1,int r=n-1){
if(mn[p]>=lim||r<lim||l>bord) return -1;
if(l==r) return l;
int mid=(l+r)>>1;
int t=jumpl(lim,bord,ls,l,mid);
if(~t) return t;
return jumpl(lim,bord,rs,mid+1,r);
}
int jumpr(int lim,int bord,int p=1,int l=1,int r=n-1){
if(mx[p]<=lim||l>lim||r<bord) return -1;
if(l==r) return r;
int mid=(l+r)>>1;
int t=jumpr(lim,bord,rs,mid+1,r);
if(~t) return t;
return jumpr(lim,bord,ls,l,mid);
}
void update(int x,int p=1,int l=1,int r=n-1){
if(l==r){mn[p]=pre[l];mx[p]=suf[r];return;}
int mid=(l+r)>>1;
if(x<=mid) update(x,ls,l,mid);
else update(x,rs,mid+1,r);
mn[p]=min(mn[ls],mn[rs]);
mx[p]=max(mx[ls],mx[rs]);
}
int qry(int p,int val){
if(!p) return 0x3f3f3f3f;
if(p>val) return min(qry(lc[p],val),p);
else return qry(rc[p],val);
}
void solve(){
n=read();m=read();
if(n==1){
for(int i=1;i<=m;++i) read(),read(),puts("0");
return;
}
ll cur=(ll)(n-1)*(n-2)>>1;
int c0=n-1,c1=0;
for(int i=1,tt=0;i<n;++i){
pre[i]=i-1;suf[i]=i+1;
pr[i]=rng();sz[i]=1;
lc[i]=rc[i]=ft[i]=0;
tt=merge(tt,i);cnt[i]=0;
}
pre[1]=1;suf[n-1]=n-1;
build();
for(int i=1;i<=n;++i) f[i]=i;
for(int i=1;i<=m;++i){
int l=read(),r=read();
if(l>r) swap(l,r);
--r;
if(l<=r){
for(int t=rt(l);t<=r;t=rt(t+1)){
if(cnt[t]==0) --c0,++c1;
else if(cnt[t]==1){--c1;f[t]=t+1;}
++cnt[t];
}
int t=jumpl(l,r);
while(~t){
int x=jump(t);
int ss=qry(x,r);
cur-=(ll)sz[x]*(sz[x]-1)>>1;
if(ss!=0x3f3f3f3f){
int a,b,c;
split(x,l-1,a,b);ft[a]=ft[b]=0;
split(b,r,b,c);ft[b]=ft[c]=0;
int l1=pre[t],l2=t,r2=pre[ss],r1=ss;
pre[l2]=l2;suf[r2]=r2;suf[l1]=r1;pre[r1]=l1;
update(l1);update(l2);update(r2);update(r1);
int nrt=merge(a,c);
cur+=(ll)sz[nrt]*(sz[nrt]-1)>>1;
cur+=(ll)sz[b]*(sz[b]-1)>>1;
}
else{
int a,b;
split(x,l-1,a,b);ft[a]=ft[b]=0;
int tt=pre[t];
suf[tt]=tt;pre[t]=t;
update(tt);update(t);
cur+=(ll)sz[a]*(sz[a]-1)>>1;
cur+=(ll)sz[b]*(sz[b]-1)>>1;
}
t=jumpl(l,r);
}
t=jumpr(r,l);
while(~t){
int x=jump(t),a,b;
cur-=(ll)sz[x]*(sz[x]-1)>>1;
split(x,r,a,b);ft[a]=ft[b]=0;
int tt=suf[t];
pre[tt]=tt;suf[t]=t;
update(tt);update(t);
cur+=(ll)sz[a]*(sz[a]-1)>>1;
cur+=(ll)sz[b]*(sz[b]-1)>>1;
t=jumpr(r,l);
}
}
printf("%lld\n",cur+(ll)c0*(i+n-1-c0)+c1);
}
}
int main(){
int tc=read();
while(tc--) solve();
return 0;
}
Anti-Median (Easy Ver.)
Easy Version 好神。不敢想像 Hard Version。
考虑如何刻画这个东西,容易发现如果强制区间长度为 3 与区间长度为 5 的限制满足,就构造不出不满足 7 的了。3 的限制告诉我们这个序列是 zig-zag 的,5 的限制看起来十分抽象,我们实际上可以发现这相当于是说奇偶位置分别单峰单谷。充分性易证,必要性考虑你一但出现上升转下降后就只能单调填了。
但这个限制还是抽象,考虑分别提取出奇偶位置 DP。我们发现将奇数位置 reverse 一下接在偶数位置后序列就双调了,至于为什么我很想画个图,但没时间,那就算了吧。
我们考虑用循环移位将最大值移到开头,这样序列就成单谷的了。后面的计数可以区间 DP,但是这样有可能算重&不满足 zig-zag 的性质。那你就在 DP 过程中保证 zig-zag 的性质,你甚至发现算重的问题也同时解决了。
#include <cstdio>
using namespace std;
int read(){
char c=getchar();int x=0;bool f=0;
while(c<48||c>57) f|=(c=='-'),c=getchar();
do x=(x<<1)+(x<<3)+(c^48),c=getchar();
while(c>=48&&c<=57);
if(f) return -x;
return x;
}
const int N=1003,M=2003,P=1000000007;
int p[N],n,ip[N],pos[N];
int f[M][M],s[M];
inline void inc(int &x,int v){if((x+=v)>=P) x-=P;}
inline bool judge(int x,int l,int r){
if(l<=x&&x<=r) return 1;
if(l<=x+n&&x+n<=r) return 1;
return 0;
}
inline int E(int x){if(x>n) return x-n;else return x;}
int lim;
inline bool check(int x,int l,int r,bool rev){
rev^=(E(x)<=lim);
int d=ip[E(x)];
if(d>1&&judge(pos[d-1],l,r)==rev) return 0;
if(d<n&&judge(pos[d+1],l,r)==rev) return 0;
return 1;
}
void solve(){
n=read();
for(int i=1;i<=n;++i) p[i]=read();
int tmp=0,res=0;
for(int i=1;i<=n;i+=2) s[++tmp]=p[i],pos[ip[tmp]=i]=tmp;
lim=tmp;
for(int i=n-(n&1);i>0;i-=2) s[++tmp]=p[i],pos[ip[tmp]=i]=tmp;
for(int i=1;i<n;++i) s[i+n]=s[i];
for(int par=0;par<2;++par){
for(int i=1;i<n+n;++i)
if(s[i]==-1||s[i]==1) f[i][i]=(E(i)<=lim)^par;
else f[i][i]=0;
for(int len=2;len<=n;++len)
for(int l=1,r=len;r<n+n;++l,++r){
f[l][r]=0;
if((s[l]==-1||s[l]==len)&&check(l,l,r,par)){
inc(f[l][r],f[l+1][r]);
if(len==n&&((E(l)>lim)^par)) inc(res,f[l+1][r]);
}
if((s[r]==-1||s[r]==len)&&check(r,l,r,par)){
inc(f[l][r],f[l][r-1]);
}
}
}
printf("%d\n",res);
}
int main(){
int tc=read();
while(tc--) solve();
return 0;
}
[CEOI 2022] Drawing
感觉非常好的一道题啊。
30-40 分是很好想的,你考虑怎么把一颗树放在平面上。你可以先随便选一个点当根,然后考虑怎么给子树分配。这个可以极角排序,每个子树分配一段区间。你发现极角排序这个东西性质很强,因为你把树放在平面上它一定被平面上这些点的凸包包含,而极角排序能保证这些点的凸包不交。至于怎么给儿子钦定一个点可以找子树凸包上面朝当前根的任意一个点。容易发现每次选最靠下的点满足条件。复杂度 \(O(n^2)\)
那这个三度的条件是来干什么的呢?边分治?但是树分治似乎很不好处理这个问题。
然后没想法,网上搜不到啥资料于是去看了官方 Editorial。觉得很精妙。
发现我们上面那个做法相当于是每次找到凸包上的一个边界点,然后构造。正解你考虑对于根所在的重链分治。你可以找凸包上相邻两个点 \(A,B\) 来对应重链两端的点,然后取一个重链的分治中心,将其固定在点 \(C\),使得 \(\triangle ABC\) 中不包含其它点。这是好做的,你找一个极角序最极端的点就行了。(图是从官解蒯的)
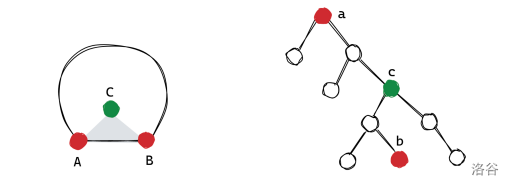
接下来关于 \(C\) 极角排序把子树分治出去就行了。
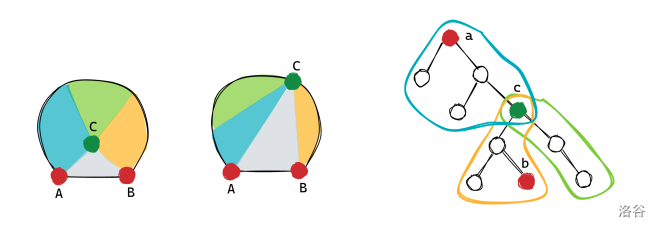
这样你就可以每次确定一个点(根)或者两个点(一个根一个叶子)然后往下递归。
按全局平衡二叉树的方法选带权中心分治,并全程 nth_element 复杂度可以做到 \(O(n\log n)\),需要很精细的实现。
为什么 Editorial 说这个算法是 \(O(n\log^2 n)\) 的呢?原来全局平衡二叉树在欧洲并不广为人知啊。在 CN 也不广为人知 CN 知道的人就挺多的。
满分代码细节好多,下午一点要还要 Ucup 所以先咕一回,也许永远不会写了。
对了,那你说为什么要保证三度的性质呢?似乎不三度也是可做的,但代码会巨大多难写。
果然沾点几何的东西代码就会细节超多。
upd: 不写了,做其它题去了。
\(O(n^2)\) 代码:
#include <cstdio>
#include <algorithm>
#pragma GCC optimize(2,3,"Ofast")
using namespace std;
const int N=200003;
typedef long long ll;
int read(){
char c=getchar();int x=0;
while(c<48||c>57) c=getchar();
do x=(x<<1)+(x<<3)+(c^48),c=getchar();
while(c>=48&&c<=57);
return x;
}
int n,sz[N];
int g[N][3],c[N];
void dfs(int u,int fa){
sz[u]=1;
for(int i=0;i<c[u];++i){
int v=g[u][i];
if(v==fa) continue;
dfs(v,u);
sz[u]+=sz[v];
}
}
int px[N],py[N];
int ox,oy;
inline bool cmp(int a,int b){return (ll)(py[a]-oy)*(px[b]-ox)<(ll)(px[a]-ox)*(py[b]-oy);}
int p[N],res[N];
inline bool cmpxy(int a,int b){
if(px[a]!=px[b]) return px[a]<px[b];
return py[a]<py[b];
}
void solve(int l,int r,int u,int fa){
int mn=min_element(p+l,p+r+1,cmpxy)-p;
if(mn>l) swap(p[mn],p[l]);
ox=px[p[l]];oy=py[p[l]];res[p[l]]=u;
int cur=l+1;
for(int i=0;i<c[u];++i){
int v=g[u][i];
if(v==fa) continue;
nth_element(p+cur,p+cur+sz[v],p+r+1,cmp);
cur+=sz[v];
}
cur=l+1;
for(int i=0;i<c[u];++i){
int v=g[u][i];
if(v==fa) continue;
solve(cur,cur+sz[v]-1,v,u);
cur+=sz[v];
}
}
int main(){
n=read();
for(int i=1;i<n;++i){
int u=read(),v=read();
g[u][c[u]++]=v;
g[v][c[v]++]=u;
}
for(int i=1;i<=n;++i){px[i]=read();py[i]=read();}
dfs(1,0);
for(int i=1;i<=n;++i) p[i]=i;
solve(1,n,1,0);
for(int i=1;i<=n;++i) printf("%d ",res[i]);
putchar('\n');
return 0;
}
Fabulous Fungus Frenzy
模拟有些细节调了一下午,感觉像是玩原神玩的。
考虑倒着做,然后相当于你可以把一块匹配区域变成通配符,发现如果一个 pattern 成功操作了一次,那么就可以消除掉这个 pattern 中的包含所有字符(即都变成通配符)。具体方式是不断把对应字母移进上一次操作形成的通配符矩形中。
发现数据范围只有 20,\(4\times 10^5\) 这个界太松了。所以暴力模拟能过。
idea 比较小清新,但是模拟就很有细节了。注意一下 swap 的时候一定不要打乱当前你想匹配的矩形中原有的点。
#include <cstdio>
#include <cctype>
#include <algorithm>
using namespace std;
const int N=23,Lim=62,M=400003;
int n,m,k,rk;
char str[N];
int f[N][N];
int h[N][N][N],np[N],mp[N];
int c[N][Lim+1];
int cnt[Lim+1];
struct Opt{
int op,x,y;
Opt(){}
Opt(int Op,int X,int Y):op(Op),x(X),y(Y){}
}seq[M];
inline void opt(int op,int x,int y){
seq[++rk]=Opt(-op,x,y);
switch(op){
case 4: swap(f[x-1][y],f[x][y]);return;
case 3: swap(f[x+1][y],f[x][y]);return;
case 2: swap(f[x][y-1],f[x][y]);return;
case 1: swap(f[x][y+1],f[x][y]);return;
}
}
inline void proc(int x){
seq[++rk]=Opt(x,1,1);
for(int i=1;i<=np[x];++i)
for(int j=1;j<=mp[x];++j){
--cnt[f[i][j]];
++cnt[f[i][j]=0];
}
}
inline int trans(char c){
if(islower(c)) return c-'a'+1;
if(isupper(c)) return c-'A'+27;
if(isdigit(c)) return c-'0'+53;
return 0;
}
bool del[N][N];
inline void mov(int ax,int ay,int bx,int by){
while(ax!=bx||ay!=by){
while(ax>bx&&!del[ax-1][ay]) opt(4,ax,ay),--ax;
while(ax<bx&&!del[ax+1][ay]) opt(3,ax,ay),++ax;
while(ay>by&&!del[ax][ay-1]) opt(2,ax,ay),--ay;
while(ay<by&&!del[ax][ay+1]) opt(1,ax,ay),++ay;
}
}
inline bool check(int x,bool ff=0){
bool fl=0;
int sum=0;
for(int i=1;i<=Lim;++i){
if(c[x][i]&&cnt[i]) fl=1;
if(c[x][i]>cnt[i]) sum+=c[x][i]-cnt[i];
}
return (fl||ff)&&sum<=cnt[0];
}
inline int pat(){
for(int i=1;i<=k;++i) if(check(i)) return i;
return -1;
}
inline pair<int,int> loc(int col){
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
if(!del[i][j]&&f[i][j]==col) return make_pair(i,j);
return make_pair(NULL,NULL);
}
inline pair<int,int> loc(int col,int x){
for(int i=1;i<=np[x];++i)
for(int j=1;j<=mp[x];++j)
if(h[x][i][j]==col) return make_pair(i,j);
return make_pair(NULL,NULL);
}
inline void flushpat(int t){
for(int i=1;i<=np[t];++i)
for(int j=1;j<=mp[t];++j){
if(cnt[h[t][i][j]]){
--cnt[h[t][i][j]];
auto [x,y]=loc(h[t][i][j]);
mov(x,y,i,j);
}
else{
--cnt[0];
auto [x,y]=loc(0);
mov(x,y,i,j);
}
del[i][j]=1;
}
for(int i=1;i<=np[t];++i)
for(int j=1;j<=mp[t];++j)
if(del[i][j]) ++cnt[f[i][j]],del[i][j]=0;
}
int main(){
scanf("%d%d%d",&n,&m,&k);
np[0]=n;mp[0]=m;
for(int i=1;i<=n;++i){
scanf("%s",str+1);
for(int j=1;j<=m;++j) ++c[0][h[0][i][j]=trans(str[j])];
}
for(int i=1;i<=n;++i){
scanf("%s",str+1);
for(int j=1;j<=m;++j) ++cnt[f[i][j]=trans(str[j])];
}
for(int x=1;x<=k;++x){
scanf("%d%d",np+x,mp+x);
for(int i=1;i<=np[x];++i){
scanf("%s",str+1);
for(int j=1;j<=mp[x];++j) ++c[x][h[x][i][j]=trans(str[j])];
}
}
int t=pat();
while(~t){
flushpat(t);proc(t);
while(true){
int cc=-1;
for(int i=1;i<=Lim;++i)
if(cnt[i]&&c[t][i]){cc=i;break;}
if(cc<0) break;
auto [ax,ay]=loc(cc);
auto [bx,by]=loc(cc,t);
mov(ax,ay,bx,by);
proc(t);
}
t=pat();
}
if(!check(0,1)){puts("-1");return 0;}
flushpat(0);
printf("%d\n",rk);
while(rk) printf("%d %d %d\n",seq[rk].op,seq[rk].x,seq[rk].y),--rk;
return 0;
}
Local Deletions
这下不会 Div.2 F 了\kk。
感觉非常妙啊其实对很多人都非常典吧,考虑的时候方向完全走错了。
容易发现操作只会进行 \(\log\) 轮,你可以建出一个类似分散层叠的结构,把全局数组每一轮修改后的结果存下来。
剩下的东西就很简单了,你发现区间询问只会影响两个端点是否往下传,于是往下递归一下就行了。
预处理前驱后继的话,复杂度 \(O(n\log n)\)。代码怎么又咕了。
启示:不是啥操作题都是让你乱找性质的。有些东西就是可以直接维护。
JOI Open 2022 放学路
会广义串并联你就会发现它的部分分十分具有指向性。
首先考虑去掉无用边,如果一条边不在任何一条 \(1\to n\) 的简单路径上这条边就可以去掉了。可以扣除圆方树上 \(1\to n\) 这条链上的所有边。
然后跑出最短路 DAG,发现如果有不在这上面的边那就一定有解。
于是考虑对着这个 DAG 做。使用广义串并联方法缩二度点如果能缩成一条 \(1\to n\) 的链显然那就是无解的,否则总能构造出解。
注意这并不是在判它是否是广义串并联图,你需要保证 \(1,n\) 不被缩点。
#include <queue>
#include <cstdio>
#include <algorithm>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/hash_policy.hpp>
using namespace std;
int read(){
char c=getchar();int x=0;
while(c<48||c>57) c=getchar();
do x=(x<<1)+(x<<3)+(c^48),c=getchar();
while(c>=48&&c<=57);
return x;
}
const int N=100003,M=200003;
typedef long long ll;
int n,m,cnt;
int hd[N],ver[M<<1],nxt[M<<1],val[M<<1],tot;
ll dis[N];
inline void add(int u,int v,int w){
nxt[++tot]=hd[u];hd[u]=tot;ver[tot]=v;val[tot]=w;
}
int eu[M],ev[M],ew[M];bool exi[M];
struct Info{
int x;ll d;
Info(int X,ll D):x(X),d(D){}
friend bool operator<(const Info a,const Info b){
return a.d>b.d;
}
};
priority_queue<Info> que;
const ll INF=0x3f3f3f3f3f3f3f3f;
namespace BCT{
int hd[M],ver[M<<1],nxt[M<<1],tot;
void add(int u,int v){
nxt[++tot]=hd[u];hd[u]=tot;ver[tot]=v;
nxt[++tot]=hd[v];hd[v]=tot;ver[tot]=u;
}
int ft[M],de[M];
void dfs(int u,int fa){
ft[u]=fa;
for(int i=hd[u];i;i=nxt[i]){
int v=ver[i];
if(v==fa) continue;
de[v]=de[u]+1;
dfs(v,u);
}
}
bool vis[M];
inline void jump(){
int u=1,v=n;
vis[u]=vis[v]=1;
while(u!=v){
if(de[u]<de[v]) swap(u,v);
vis[u=ft[u]]=1;
}
}
bool check(int u,int v){
if(ft[u]==ft[v]) return vis[ft[u]];
if(de[ft[u]]>de[ft[v]]) return vis[ft[u]];
return vis[ft[v]];
}
}
int low[N],dfn[N],num;
int stk[N],tp;
int d[N];
inline void chmn(int &x,int v){if(x>v) x=v;}
void tarjan(int u){
low[u]=dfn[u]=++num;stk[++tp]=u;
for(int i=hd[u];i;i=nxt[i]){
int v=ver[i];
if(dfn[v]) chmn(low[u],dfn[v]);
else{
tarjan(v);
chmn(low[u],low[v]);
if(low[v]>=dfn[u]){
++cnt;int x;
do BCT::add(x=stk[tp--],cnt+n);while(x!=v);
BCT::add(u,cnt+n);
}
}
}
}
__gnu_pbds::gp_hash_table<int,bool> mp[N];
int main(){
n=read();m=read();
for(int i=1;i<=m;++i){
int u=read(),v=read(),w=read();
eu[i]=u;ev[i]=v;ew[i]=w;
add(u,v,w);add(v,u,w);
}
tarjan(1);
BCT::dfs(1,0);BCT::jump();
for(int i=1;i<=n;++i) dis[i]=INF;
que.emplace(1,dis[1]=0);
while(!que.empty()){
auto [u,d]=que.top();que.pop();
if(d>dis[u]) continue;
for(int i=hd[u];i;i=nxt[i]){
int v=ver[i],w=val[i];
if(dis[v]>d+w) que.emplace(v,dis[v]=d+w);
}
}
for(int i=1;i<=m;++i)
if(BCT::check(eu[i],ev[i])){
if(dis[eu[i]]>dis[ev[i]]) swap(eu[i],ev[i]);
if(dis[eu[i]]+ew[i]!=dis[ev[i]]){puts("1");return 0;}
if(!mp[eu[i]][ev[i]]){
++d[eu[i]];++d[ev[i]];
mp[eu[i]][ev[i]]=mp[ev[i]][eu[i]]=1;
}
}
queue<int> que;
for(int i=2;i<n;++i) if(d[i]==2) que.emplace(i);
while(!que.empty()){
int u=que.front();que.pop();
if(d[u]!=2) continue;
int a=0,b=0;
for(auto [x,c]:mp[u])
if(c){
if(b) a=x;
else b=x;
}
mp[a][u]=mp[b][u]=0;
mp[u].clear();
if(!mp[a][b]) mp[a][b]=mp[b][a]=1;
else{
if(--d[a]==2&&a!=1&&a!=n) que.emplace(a);
if(--d[b]==2&&b!=1&&b!=n) que.emplace(b);
}
}
for(int i=1;i<=n;++i) if(d[i]>2){puts("1");return 0;}
for(int i=2;i<n;++i) if(d[i]==1){puts("1");return 0;}
puts("0");
return 0;
}
JOI Open 2022 跷跷板
还挺有意思的。感觉自己的做法切入手段有点不太一样。
发现题目让你最小化极差,那么我们把它转化成一个路径模型。
建一个三角形,最上面那个点代表区间 \([1,n]\),然后对于区间 \([l,r]\) 每次你可以向左下走到 \([l,r-1]\) 和向右下走到 \([l+1,r]\)。每个点的点权设置为所代表区间的平均值。
然后你发现这个三角形满足一些显然的偏序关系,同一层的点权递增,下一层的两个点夹着的本层点点权也一定被下一层的那两个点的点权夹着。
那么你从第一层走到最后一层时,我们在 \([1,n]\) 所代表的点权位置画一条竖线,那么只有这条竖线前面那个和后面那个点会被走到。证明可以考虑如果不是这两个点的话,那么上一层你往更靠近竖线的位置走一定更优,因为你一定不会超过竖线。
于是我们求出全局平均值在每一层的前驱后继(这部分可以 \(O(n)\) 但是我偷懒了)。接下来每一层的点权只有两种选择,此时最小化极差是经典题。先考虑全部选更靠左的,然后按点权从小到大逐渐变成选靠右的,容易发现任何时候你选的点正好构成了一条路径。用某些数据结构简单维护极差即可。
#include <set>
#include <cstdio>
#include <algorithm>
using namespace std;
int read(){
char c=getchar();int x=0;
while(c<48||c>57) c=getchar();
do x=(x<<1)+(x<<3)+(c^48),c=getchar();
while(c>=48&&c<=57);
return x;
}
const int N=200003;
typedef long long ll;
typedef __int128 lll;
int n,rk;
ll s[N];
int f[N];
double a[N],b[N];
bool ch[N];
struct Pos{
double vl;int x;
friend bool operator<(const Pos a,const Pos b){
return a.vl<b.vl;
}
}e[N];
multiset<double> st;
void upd(int x){
st.erase(st.find(a[x]));
st.emplace(b[x]);
}
int main(){
n=read();
for(int i=1;i<=n;++i) s[i]=s[i-1]+read();
for(int m=n-1;m;--m){
int l=0,r=n-m+1;
while(l<r){
int p=(l+r)>>1;
if((lll)(s[p+m]-s[p])*n<=(lll)s[n]*m) l=p+1;
else r=p;
}
f[m]=l;
}
st.emplace((double)s[n]/n);
for(int i=1;i<n;++i){
int p=f[i];
a[i]=(double)(s[p+i-1]-s[p-1])/i;
b[i]=(double)(s[p+i]-s[p])/i;
if(p){
ch[i]=0;
st.emplace(a[i]);
if(p+i<=n) e[++rk]=(Pos){a[i],i};
}
else{
ch[i]=1;
st.emplace(b[i]);
}
}
sort(e+1,e+rk+1);
double res=1e18;
res=min(res,*prev(st.end())-*st.begin());
for(int i=1;i<=rk;++i){
upd(e[i].x);
res=min(res,*prev(st.end())-*st.begin());
}
printf("%.10lf\n",res);
return 0;
}
AGC043C Giant Graph
好像记得 zhy 给我提过这个题。这个题有点神奇,但是 kenkoooo 只评了下位红。
也许是我真的想不到这种套路吧。
题目相当于求三张图的笛卡尔积的最大权独立集。然而点权相差巨大,这往往意味着所谓的“最大权”实际上就是“最大字典序”。
于是我们按 \(i+j+k\) 从大往小能选则选,就可以得到最大权独立集了!
考虑你怎么刻画能选就选这个过程。将边按照点权大小定向成 DAG 后,我们其实这就是在求这个 DAG 的核。
于是最抽象的一步来了,DAG 的核的组合意义是在上面进行有向图博弈的所有 P 状态。而根据 SG 定理你可以把它拆成三个图子游戏,把 SG 值异或起来就可以刻画三张图笛卡尔积的 SG 函数了。
剩下的统计很简单,你当然可以异或卷积,但是注意到稀疏无环有向图的 \(SG\) 函数是 \(O(\sqrt m)\) 级别的,暴力枚举两维值域即可通过。复杂度竟然线性。
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
int read(){
char c=getchar();int x=0;
while(c<48||c>57) c=getchar();
do x=(x<<1)+(x<<3)+(c^48),c=getchar();
while(c>=48&&c<=57);
return x;
}
const int N=100003,P=998244353,W=716070898;
typedef long long ll;
int n,m;
vector<int> vec[N];
int pw[N],sg[N];
bool vis[N];
inline void inc(int &x,int v){if((x+=v)>=P) x-=P;}
inline void solve(int *cnt){
for(int u=n;u;--u){
sg[u]=0;
for(int v:vec[u]) vis[sg[v]]=1;
while(vis[sg[u]]) ++sg[u];
for(int v:vec[u]) vis[sg[v]]=0;
vec[u].clear();
inc(cnt[sg[u]],pw[u]);
}
}
int w[3][N];
int main(){
n=read();pw[0]=1;
for(int i=1;i<=n;++i) pw[i]=(ll)pw[i-1]*W%P;
for(int t=0;t<3;++t){
m=read();
while(m--){
int u=read(),v=read();
if(u>v) swap(u,v);
vec[u].emplace_back(v);
}
solve(w[t]);
}
int res=0;
for(int i=0;i<=1000;++i)
for(int j=0;j<=1000;++j)
res=(res+(ll)w[0][i]*w[1][j]%P*w[2][i^j])%P;
printf("%d\n",res);
return 0;
}
所以 SG 定理有另一种形式化描述:\(SG(G_1\times G_2)=SG(G_1)\oplus SG(G_2)\)
说起来所谓图的“笛卡尔积”就是为了刻画“将两张图的子状态拼起来”(子游戏)这个东西呢!
USACO22OPEN P 组 Hoof and Brain
神奇题。华为云计算挑战赛的时候就卡过缩点博弈题,这里再卡一次,紫菜紫菜。
啊你发现这个题解决常规博弈的手段全都用不了啊!在 SCC DAG 上讨论度数讨论了很久都没有出结果。这提示我们要从博弈本身的性质入手去做了!
没出度的点显然 Hoof 不会往那走,用拓扑全部删了。
假设不存在一出度点,那么显然 Hoof 可以永远走下去。有一出度点呢?那么这个一出度点出边不能被堵。相当于是说这个点和它指向的点一共只能有不超过一个棋子!
那么你可以直接把这两个点看成单点。于是一直缩点下去,缩完之后图上只剩下多于一条出边的点和有自环的点。如果缩完点之后两个棋子不在一个点,发现 Hoof 合理决策是可以永远走下去的。
复杂度暴力合并入边集合可能是 \(O(n^2)\) 的。考虑它想卡你只能造一条长链来堆积入边,所以说你就直接用优先队列每次取出入边集合最小的做。复杂度感觉同启发式合并 \(O(n\log n)\)。
当然题解做法是直接启发式合并入边集合。我咋没想到这么 trivial 的方法呢?写一写,发现这样写并查集细节更多了,没有调过去,还是我的做法更好写!!!
#include <queue>
#include <cstdio>
#include <cassert>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/hash_policy.hpp>
using namespace std;
int read(){
char c=getchar();int x=0;
while(c<48||c>57) c=getchar();
do x=(x<<1)+(x<<3)+(c^48),c=getchar();
while(c>=48&&c<=57);
return x;
}
int n,m;
const int N=100003;
__gnu_pbds::gp_hash_table<int,bool> g[N];
int d[N],f[N],nx[N];
int rt(int x){
if(f[x]==x) return x;
return f[x]=rt(f[x]);
}
struct cmp{
bool operator()(const int a,const int b){
return g[a].size()>g[b].size();
}
};
queue<int> que;
priority_queue<int,vector<int>,cmp> pq;
int main(){
n=read();m=read();
for(int i=1;i<=m;++i){
int u=read(),v=read();
++d[u];g[v][u]=1;nx[u]^=v;
}
for(int i=1;i<=n;++i){
f[i]=i;
if(!d[i]) que.emplace(i);
}
while(!que.empty()){
int u=que.front();que.pop();
for(auto [v,c]:g[u]){
nx[v]^=u;
if(!--d[v]) que.emplace(v);
}
g[u].clear();
}
for(int i=1;i<=n;++i) if(d[i]==1) pq.emplace(i);
while(!pq.empty()){
int u=pq.top();pq.pop();
int v=nx[u];
if(u==v) continue;
f[u]=v;
for(auto [x,c]:g[u]){
nx[x]^=u;
if(g[v].find(x)!=g[v].end()){
if(--d[x]==1) pq.emplace(x);
}
else{
g[v][x]=1;
nx[x]^=v;
}
}
g[u].clear();
}
int q=read();
while(q--){
int u=read(),v=read();
if(!d[u]||!d[v]||rt(u)==rt(v)) putchar('B');
else putchar('H');
}
putchar('\n');
return 0;
}

