[PR #5] 和平共处（RuCode 2020 Division A+B. I）

给定平面上的若干个黑点，接下来动态加入白点，你需要再每次加入之后输出至少删多少个点才能使得不存在一个黑点在白点的右上方。

前言

将冲突的黑白点连边，不难发现这道题本质是让我们求动态最小点覆盖。

认认真真学习了一下这道题相关的做法以及有关的二分图网络流理论，感觉自己又刷新了一些东西的理解。

所以说我们就从普通的二分图匹配开始吧！

再探二分图匹配

众所周知，二分图最大匹配可以用网络流 Dinic 算法做到 \(O(m\sqrt n)\) 的复杂度。

在某些特定的图下，我们有一种“贪心流”算法。比如说对于左部点只向右部点的前缀连边。这个是后我们考虑经典的贪心思想，先解决限制紧的。于是我们按照连边前缀长度从小到大排序，每次随便每个左部点选一种流操作就行了。

更多的情况下，我们需要处理“区间流”，即一个点向右边一个区间连边。

而对于和平共处这道题，一个白点向右上角所有黑点连边，它相当于需要解决“二维偏序结构流”，容易发现区间流本质上也是一种二维偏序结构流（前缀流则是一维偏序）。

这种流我们处理的手段依旧是考虑最紧的限制。按一维排序后，每次选择另一维还有流的所有点中最靠边的流。

由于 zhy 喜欢反反复复提到这个东西，所以在平时我也会经常去有限考虑某道题目能否转化成贪心流问题做。

再探柯尼希定理

学二分图时，你可能只是听说过二分图最大匹配等于最小点覆盖这样奇奇怪怪的一些结论，也可能去了解过它的一些形式化一点的证明。但是这个证明对于我来说有点太构造性了，于我的意义仅仅只是多知道了最小点覆盖的构造方式。

你可能还了解过最大流最小割定理，一个最大一个最小两极相通，你总觉得这跟二分图中的什么东西很像，但是说不上来。

记得在成七集训时我碰到了一道求最小点覆盖题，我的想法是按着柯尼希定理的证明来，先构造最大匹配，然后在上面 dfs 构造最小点覆盖。而我发现了一种甚至不要 dfs 的写法，注意到最小点覆盖问题可以用类似文理分科的模型最小割建模，与普通二分图建模的区别仅仅是中间边权全部是无限。这样的话，只要看一下最小割上有哪些边就可以构造出最小点覆盖了。

这代表最小点覆盖与最小割是相通的。利用这个建模，我们将跑完流之后的图源点所能到达的点称为 \(A\) 集，能到汇点的点称为 \(B\) 集，左右部点集分别设为 \(L,R\)。设 \(A_l=A\cap L,A_r=A\cap R\)，\(B_l,B_r\) 同理。

那么我们就刻画出了如下的一张图：

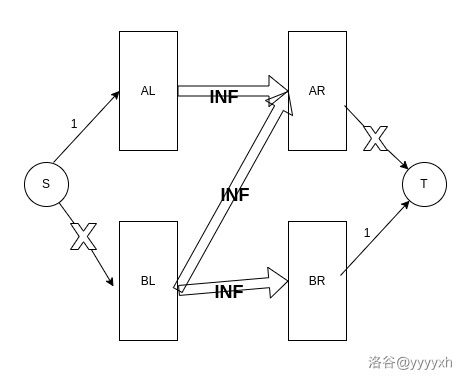
这张图统一了最大匹配与最小点覆盖的关系。我们借助最大流最小割定理，可以看出最大匹配和最小割都是 \(|A_l|+|B_r|\)，而由于 \(A_l\) 与 \(B_r\) 之间没有任何边，所以 \(A_r\cup B_l\) 是一个最小点覆高。这部分可以参考 rqy 博客。

你说，啥？这不是把形式化证明用图画出来了而已吗？不过我们可以从这张图上发掘出更多意想不到的性质。

比如，你发现最大匹配在这张图如何被体现出来呢？你可以说明 \(B_l\) 与 \(A_r\) 之间虽然有边，但它一定不会位于任何一种最大匹配中，否则这条匹配边会占去 \(A_r\cup B_r\) 中的两个位置，剩下的就凑不出那么多匹配边了。

再探匈牙利算法

匈牙利算法有什么好再探的呢？我们记得，匈牙利算法有一个很好的性质，就是一个左部点匹配了之后一定不会失去匹配。当我们把目光从有哪些边在匹配里移向有哪些点在匹配中时，这个性质显得至关重要。

如果顺序枚举左部点，我们发现匈牙利算法正好求出了一个匹配点集同时满足字典序最小且大小最大。感觉和 kruskal 算法很像呀！明明是求总和最大，怎么同时又求出来了字典序最小的呢？这提示着我们，我们遇到了一个经典的组合结构：拟阵。

英文 Tutorial 里面称这个拟阵为 transversal matroid（横向拟阵）。

拟阵结构还有一些其它征兆，比如说你一个集合塞得不能满时，你可以”加一换一“。比如说图拟阵你可以加入一条边然后去掉一条环上的边，transversal matroid 你可以通过增广一条“增广环”来“加一换一”。

题解做法

我们终于开始讲这道题了。根据匈牙利算法或者直接说根据拟阵的性质，我们可以按白点的加入顺序增广，得到一个匹配的白点集合字典序最小的流法，来判断每一次答案是否 +1。复杂度可以直接做到 \(O(n^2\sqrt n)\)。

然而注意到这道题的流是贪心流，我们可以在 \(O(n\log n)\) 的时间内求单次流，但这能帮助我们求出字典序最小的流法吗？事实上，任意一种可以构造点覆盖的网络流算法套上整体二分都可以求匹配点集字典序最小的匹配。

我们维护还没确定是否在最优方案中的左部点集合 \(S_1\)，已经确定了的左部点集合 \(S_2\) 和右部点集合 \(S_3\)。需要保证 \(\max(S_2)<\min(S_1)\) 即已经确定的集合是一个前缀。

每次我们将 \(S_1\) 分成尽可能均匀值域不交的两半 \(X,Y\)，然后对新图 \(G'=(S_2\cup X,S_3)\) 构造如上面那个图片的最小点覆盖，并且区分出 \(A_l,A_r,B_l,B_r\) 四个集合。

我们说明，新图 \(A'=(A_l,A_r)\) 的最优匹配和 \(B'=(B_l\cup Y,B_r)\) 的最优匹配并起来就是全局最优匹配。首先我们可以发现 \((A_l,A_r)\) 和 \((B_l\cup Y,B_r)\) 并起来一定是 \(G'\) 的最优匹配。

因为根据我们上面讲的，\(B_l\) 与 \(A_r\) 之间一定不会有匹配边，而 \(B_r\) 与 \(A_l\) 之间压根就没有边！

接下来用匈牙利算法一样的方式增广 \(Y\) 中的节点，发现这样一定不会影响 \(A'\) 已有的匹配，因为 \(A'\) 中的匹配已经锁得死死的了：每一个右部点都有匹配，而每一个左部点，只向 \(A_r\) 中点连边！

于是我们就可以欢乐地递归下去，然而我们发现我们如果直接把 \(B_l\cup Y\) 往下递归，集合不一定减半，复杂度好假？？？

这时候又要请出我们的最小割刻画，我们发现 \(B_l\) 一定是满匹配的，而 \(Y\) 又比 \(G'\) 左部点中所有数都大，所以说根据匈牙利算法的结论我们一定不会丢掉 \(B_l\) 中的匹配。

所以往右边递归时，我们可以把整个 \(B_l\) 扔到 \(S_2\) 中去！

本题中如何构造最小点覆盖呢？可以用上面讲的贪心流，然后线段树优化建图跑 dfs 在残量网络上求最小点覆盖。

也可以考虑从左到右决策，对于每个黑点你需要决策它要不要把限制收紧到这个点，线段树维护用主席树构造方案。

我实际写的做法

你可以发现上面那坨与下面写的代码不符，是因为贪心流+线段树优化建图+整体二分一看就码量上天。于是我又在网上找了个简单做法。

一个做法用来学，一个做法用来给 tham 交差。

你会发现上面那个做法虽然是标算但是完全没用黑白点二维偏序结构的性质。而我们可以发现，随着白点不断加入，一个黑点只有可能从选变成不选，而一个白点只会从不选变成选。所以你可以整体二分求出某个时刻的点覆盖之后，你看一下每个点选没选，然后你就知道这个点需要到哪边去决策。

怎么求点覆盖构造方案呢？跟上面一样贪心流+线段树优化建图。

有一个抽象至极的做法：贪心流本质求出了每一个黑点右边第一个比它高且能匹配的白点，你考虑用这个东西来决策每个黑点要不要选，如果当前黑点的匹配跨过了限制或者说压根没有匹配，你就选这个黑点。离谱的是手玩一下你发现这竟然是对的，而且还依赖了贪心流求出的匹配的性质。

记得开 multimap。

#include <map>
#include <cstdio>
#include <algorithm>
using namespace std;
int read(){/*...*/}
const int N=200003;
int n,m;
struct Pos{
	int x,y,id;
	friend bool operator<(const Pos a,const Pos b){
		if(a.x!=b.x) return a.x<b.x;
		if(a.y!=b.y) return a.y<b.y;
		return a.id<b.id;
	}
}s[N],sl[N],sr[N];
int res[N],mat[N];
void solve(int vl,int vr,int l,int r,int cur){
	if(vl>vr) return;
	int mid=(vl+vr)>>1;
	multimap<int,int> mp;
	for(int i=r;i>=l;--i)
		if(s[i].id){
			if(s[i].id<=mid) mp.emplace(s[i].y,i);
		}
		else{
			auto it=mp.lower_bound(s[i].y);
			if(it==mp.end()){mat[i]=0;continue;}
			mat[i]=it->second;
			mp.erase(it);
		}
	int lef=0,nl=0;
	int rig=0,nr=0;
	int lim=0x3f3f3f3f;
	for(int i=l;i<=r;++i){
		if(s[i].id){
			if(s[i].id<=mid&&s[i].y<lim) sl[++nl]=s[i],++lef;
			else sr[++nr]=s[i];
		}
		else{
			if(!mat[i]||s[mat[i]].y>=lim) lim=min(lim,s[i].y);
			if(s[i].y>=lim) sr[++nr]=s[i],++rig;
			else sl[++nl]=s[i];
		}
	}
	for(int i=1;i<=nl;++i) s[l+i-1]=sl[i];
	for(int i=1;i<=nr;++i) s[l+nl+i-1]=sr[i];
	res[mid]=lef+rig+cur;
	solve(vl,mid-1,l,l+nl-1,cur+rig);
	solve(mid+1,vr,r-nr+1,r,cur+lef);
}
int main(){
	n=read();
	for(int i=1;i<=n;++i){s[i].x=read();s[i].y=read();s[i].id=0;}
	m=read();
	for(int i=1;i<=m;++i){s[i+n].x=read();s[i+n].y=read();s[i+n].id=i;}
	sort(s+1,s+n+m+1);
	solve(1,m,1,n+m,0);
	for(int i=1;i<=m;++i) printf("%d\n",n+i-res[i]);
	return 0;
}