第七章:递推、线性dp、背包问题、区间dp(7.27、7.28)
线性dp:
NC16708 过河卒
noip2002的题,注意LL和数组下标不要越界

#include<bits/stdc++.h> #define LL long long using namespace std; LL mp[30][30],dp[30][30]; int main() { int n,m,x,y;scanf("%d%d%d%d",&n,&m,&x,&y); if(x-1>=0&&y-2>=0)mp[x-1][y-2]=1; if(x-2>=0&&y-1>=0)mp[x-2][y-1]=1; if(x-1>=0)mp[x-1][y+2]=1; if(y-2>=0)mp[x+1][y-2]=1; if(x-2>=0)mp[x-2][y+1]=1; if(y-1>=0)mp[x+2][y-1]=1; mp[x+1][y+2]=1,mp[x+2][y+1]=1; mp[x][y]=1; dp[0][0]=1; dp[0][0]=1; for(int i=0;i<=n;i++) for(int j=0;j<=m;j++) { if(!mp[i+1][j])dp[i+1][j]+=dp[i][j]; if(!mp[i][j+1])dp[i][j+1]+=dp[i][j]; } printf("%lld\n",dp[n][m]); }
NC16619 传球游戏
dp[ i ][ j ]表示传了j次后到达i的方法数
dp[ i ][ j ]=dp[ i-1 ][ j-1 ] + dp[ i+1 ][ j-1 ];
NC16810 [NOIP1999]拦截导弹
求最长的不上升子序列的长度
求原序列最少可划分为多少不上升子序列
NC16664 [NOIP2004]合唱队形
从左向右和从右向左分别求一次最长上升子序列
ans = max(dpl[ i ] + dpr[ i ]) - 1
NC235954 滑雪
记忆化搜索
NC235948 最大子串和
字串和,用f[ i ]去记录,每次a[ i ]和f[ i-1 ]+a[ i ]取max就好
NC235624 牛可乐和最长公共子序列
LCS
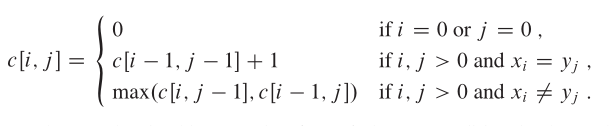
背包问题:
二位费用背包:
NC14699 队伍配置
dp[ i ][ j ][ k ]表示cost为i时,选了j个从者,k个概念礼装的最大ATK
先选从者,再选概念礼装
//从者 for(int i=1;i<=n;i++) { int x,y;scanf("%d%d",&x,&y); for(int j=d;j>=y;j--) for(int k=1;k<=5;k++) dp[j][k][0]=max(dp[j][k][0],dp[j-y][k-1][0]+x),ans=max(ans,dp[j][k][0]); } //概念礼装 for(int i=1;i<=m;i++){ int x,y;scanf("%d%d",&x,&y); for(int j=d;j>=y;j--) for(int k=1;k<=5;k++) for(int l=1;l<=k;l++) dp[j][k][l]=max(dp[j][k][l],dp[j-y][k][l-1]+x),ans=max(ans,dp[j][k][l]); }
map优化超大背包:
NC235951 草药大师
w和v都很大的时候使用map去优化

#include<bits/stdc++.h> #define LL long long using namespace std; map<int,LL>mp,tmp; map<int,LL>::iterator it; int main() { int n,m;scanf("%d%d",&n,&m); mp.clear();mp[0]=0; for(int i=1;i<=n;++i) { int v,w;scanf("%d%d",&w,&v); tmp.clear(); for(it=mp.begin();it!=mp.end();++it) { int x=it->first; LL y=it->second; if(tmp.find(x)==tmp.end())tmp[x]=y; else tmp[x]=max(tmp[x],y); if(x+w<=m)tmp[x+w]=max(tmp[x+w],y+v); } mp.clear(); LL ans=-1; for(it=tmp.begin();it!=tmp.end();++it) if(it->second>ans) { mp[it->first]=it->second; ans=it->second; } if(i==n)printf("%lld\n",ans); } }
区间dp:
区间DP是先枚举长度,再枚举起点,然后在起点和终点之间枚举中间点,表示合并的两个区间
NC50493 石子合并
dp[ i ][ j ]为合并[ i , j ]区间的最小得分
dp[ i ][ j ] = min(dp[ i ][ k ] + dp[ k+1 ][ j ] + sum( i , j ))
求max同理
因为是环形,所以记得断环乘2
NC235246 田忌赛马
贪心+区间dp

#include<bits/stdc++.h> #define LL long long using namespace std; bool cmp(const int x,const int y){return x>y;} int a[5003],b[5003],dp[5003][5003]; int check(int x,int y) { if(x>y)return 200; if(x==y)return 0; return -200; } int main() { int n;scanf("%d",&n); for(int i=1;i<=n;++i)scanf("%d",&a[i]); sort(a+1,a+1+n,cmp); for(int i=1;i<=n;++i)scanf("%d",&b[i]); sort(b+1,b+1+n); memset(dp, -0x3f, sizeof(dp)); for(int len=1;len<=n;++len) for(int i=1;i+len-1<=n;++i) { int j=i+len-1; int k=len; if(len==1)dp[i][j]=check(a[i],b[k]); else dp[i][j]=max(dp[i+1][j]+check(a[i],b[k]),dp[i][j-1]+check(a[j],b[k])); } printf("%d\n",dp[1][n]); }
NC13230 合并回文子串
dp[ i ][ j ][ k ][ l ] A的[ i,j ]和B的[ k,l ]能不能组成回文串
转移的时候两两匹配(四种情况),还要关注中间的是否是回文串

#include<bits/stdc++.h> #define LL long long using namespace std; char a[55],b[55]; int dp[53][53][53][53]; int main() { int T;scanf("%d",&T); while(T--) { int ans=0; memset(dp,0,sizeof(dp)); scanf("%s",a+1); scanf("%s",b+1); int l1=strlen(a+1); int l2=strlen(b+1); for(int d1=0;d1<=l1;++d1) for(int d2=0;d2<=l2;++d2) for(int i=1,j=d1;j<=l1;++i,++j) for(int k=1,l=d2;l<=l2;++k,++l) { if(d1+d2<=1)dp[i][j][k][l]=1; else { dp[i][j][k][l]=0; if(a[j]==a[i]&&d1>1) if(dp[i+1][j-1][k][l]) dp[i][j][k][l]=1; if(a[j]==b[k]&&d1&&d2) if(dp[i][j-1][k+1][l]) dp[i][j][k][l]=1; if(b[l]==a[i]&&d1&&d2) if(dp[i+1][j][k][l-1]) dp[i][j][k][l]=1; if(b[l]==b[k]&&d2>1) if(dp[i][j][k+1][l-1]) dp[i][j][k][l]=1; } if(dp[i][j][k][l])ans=max(ans,d1+d2); } printf("%d\n",ans); } }
NC16645 [NOIP2007]矩阵取数游戏
可以看出每一行之间是不相关的,转化为行内的区间dp问题
注意会爆long long,用__int128

#include<bits/stdc++.h> #define LL __int128 using namespace std; LL a[100],dp[100][100]; int n,m; void print(LL x) { if(x<0){putchar('-');x=-x;} if(x/10)print(x/10); putchar(x%10+'0'); } LL ksm(LL x,LL y) { LL res=1; while(y) { if(y&1)res*=x; x=x*x;y/=2; } return res; } LL work() { for(int i=1;i<=m;++i) for(int l=1,r=i;r<=m;++l,++r) dp[l][r]=max(dp[l+1][r]+a[l]*ksm(2,m-i+1),dp[l][r-1]+a[r]*ksm(2,m-i+1)); return dp[1][m]; } int main() { scanf("%d%d",&n,&m); LL ans=0; for(int i=1;i<=n;++i) { memset(dp,0,sizeof(dp)); for(int j=1;j<=m;++j) scanf("%lld",&a[j]); ans+=work(); } print(ans); }
NC207781 迁徙过程中的河流
先时间从小到大排序
dp[i]表示前i个人已过河的最短时间
前i-1个人已经过河,就让第一个把船开回去再一起回来
前i-2个人已经过河,就让1先开回去,把最后两个人送回来后,2再过去把1接回来

#include<bits/stdc++.h> #define LL long long using namespace std; LL dp[100005],t[100005]; int main() { int n;scanf("%d",&n); for(int i=1;i<=n;++i)scanf("%lld",&t[i]); sort(t+1,t+1+n); dp[1]=t[1]; dp[2]=t[2]; for(int i=3;i<=n;++i) dp[i]=min(dp[i-1]+t[1]+t[i],dp[i-2]+t[i]+t[1]+2*t[2]); printf("%lld\n",dp[n]); }






