高斯消元

模板题

用于求n个n元一次方程的解。O（n^3）

先说一下算法的过程，其实整个过程就是加减消元

先给出三个三元一次方程

手推可得到x=3，y=2，z=1。

可把系数和得到的值抽象成一个系数矩阵：

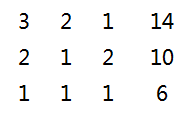
我们考虑依次消元，先把x消掉

保证精度，我们尽量把大的系数变化再在小的里加减，为了在程序中好写，把第i项最大的系数（绝对值）所在行提到第i行

然后就是用第i行的第i项系数和同一列的系数的加减消元，分别根据第二行和第三行的系数，第一行变为了

1   2/3   1/3     14/3 （对应第二行）

2   4/3   2/3     28/3 （对应第三行）

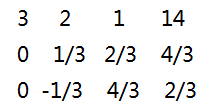
然后消掉x后，我们考虑消y，先把y的系数最大的换到第2行（从第2行开始看）

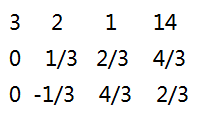
然后去消其他两行的y

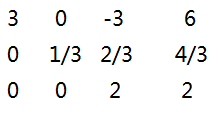
最后还要处理关于z，因为是最后一行所以就没法换行的位置

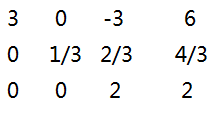
最后每一项的值即为当行的a[i][n+1]/a[i][i]

#include<bits/stdc++.h>
#define LL long long
#define N 102
using namespace std;
int read()
{
    int x=0,f=1;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    return x*f;
}
double a[N][N];
int main()
{
    int n=read();
    for(int i=1;i<=n;++i)
      for(int j=1;j<=n+1;++j)
        scanf("%lf",&a[i][j]);
    for(int i=1;i<=n;++i)//枚举列（项） 
    {
        int maxx=i;
        for(int j=i+1;j<=n;++j)//选出该列最大系数 
          if(fabs(a[j][i])>fabs(a[maxx][i]))
            maxx=j;
        if(i!=maxx)swap(a[i],a[maxx]);//并放在第i行，第i行对应了第i项答案 
        if(a[i][i]==0){printf("No Solution\n");return 0;}//最大值等于0则说明该列都为0，肯定无唯一解 
         for(int j=1;j<=n;++j)//每一项都减去一个数（就是小学加减消元）
        {
            if(j==i)continue;//当行不减，因为用这一行去更新其他行 
            double tmp=a[j][i]/a[i][i];//倍数 
            for(int k=i+1;k<=n+1;++k)//从i+1开始 
              a[j][k]-=a[i][k]*tmp;//其实就是a[j][k]-=a[j][i]*a[i][k]/a[i][i];
        }  
    }
    //上述操作结束后，矩阵会变成这样
    /*
    k1*a=e1
    k2*b=e2
    k3*c=e3
    k4*d=e4
    */
    //所以输出的结果要记得除以该项系数，消去常数
    for(int i=1;i<=n;++i)
      printf("%.2lf\n",a[i][n+1]/a[i][i]); 
} 
/*
3
2 1 2 10
1 1 1 6
3 2 1 14
*/