次小生成树
最小生成树很好求，那么对于次小生成树要怎么求呢？
稍加思考，我们可以想到，次小生成树与最小生成树差的只是一条边。
为什么呢？我们先建出一棵最小生成树，满足使用的边都是最小的，剩下的边（称为非树边）一定没有树边优。如果我们加入一条非树边，删除最小生成树中的一条边，次小生成树一定是包括在以这种方法建出的树中的（倘若删两条树边加两条非树边，则肯定没有删一条加一条优，绝不是次小生成树）
于是，我们可以这样操作：
对于每一条非树边，其边的两端点为x，y。将其加入到最小生成树中，则一定会构成一个环
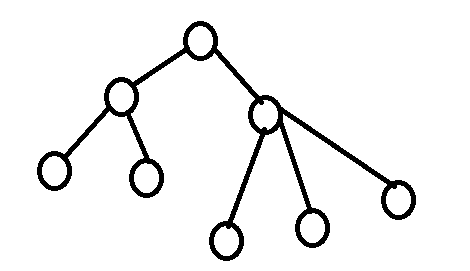
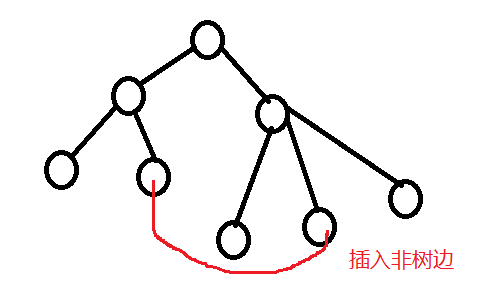
如果这时删除这个环中的最大的边（当然不能是插入的边）就构成了必须加入红色边的最小生成树。
注意：一定是删除环中最大的边，这样才保证新生成的树与原来的树相差最小，才可能为次小生成树。
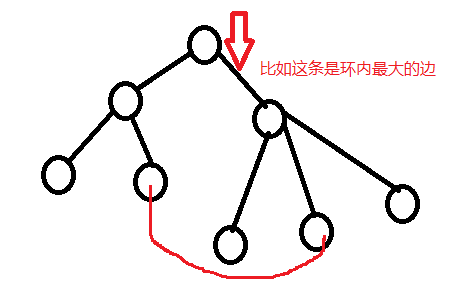删去--->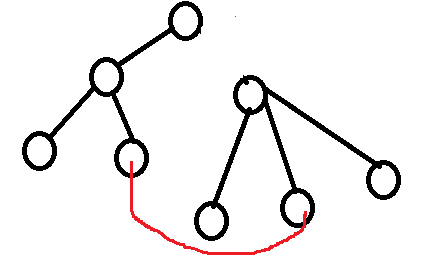
仍然是一棵树，且是必须加入红色边的最小生成树，则有可能是次小生成树
现在差不多已经明白了思想，就要看怎么实现了。得知了红色边的端点x，y，我们就可以找到它所在的环，观察图，发现从x到lca，再到y就构成了它所在的环。于是实现的难点就在于怎么快速的找到某个环内最大的边。
也就是说，寻找从x到y这条路径上的最大边（还没加入红色边呢，还没成环，因此看路径）
问题转化成：寻找树上某条路径上的最大边。
这样实现就比较好想了，我们可以用树上倍增处理处树上路径的最大边：maxx[x][i]=max（maxx[f[x][i-1]]][i-1]，maxx[x][i-1]），maxx存的是最大路径值。
求（x，y）的路径最大值就从x跳到lca，从y跳到lca，两者取个max就行。
但是，你以为这样这道题就结束了吗？QAQ
我们再看题，发现题目是严格次小生成树，也就是说，新生成的树一定得比最小生成树大，而不是大于等于。如果加入的红边的长度等于删去的边的长度就。。。wawawa（题中并没有说所以边的长度不同哦）
于是针对这种情况，我们还要再考虑考虑怎么办。
我们可以这样处理，对于树上的路径，我们不仅维护一个最大边，还维护一个次大边，这样当最大边等于红边时，不可以删最大边了，我们还可以删去次大边。
那么在倍增的时候注意一下维护细节就好。
for(int j=1;j<=20;++j) { if(dep[v]<(1<<j))break;//注意：如果深度小于向上走的步数就可以break掉了 f[v][j]=f[f[v][j-1]][j-1];//f是向上走到达的点 max1[v][j]=max(max1[v][j-1],max1[f[v][j-1]][j-1]);//max1是最大边 if(max1[v][j-1]==max1[f[v][j-1]][j-1]) g[v][j]=max(g[v][j-1],g[f[v][j-1]][j-1]);//g是次大边 else { g[v][j]=min(max1[v][j-1],max1[f[v][j-1]][j-1]); g[v][j]=max(g[v][j],g[f[v][j-1]][j-1]); g[v][j]=max(g[v][j-1],g[v][j]); } }
放出完整代码
#include<bits/stdc++.h> #define INF 2100000001 #define M 300003 #define N 100003 #define LL long long using namespace std; int read() { int f=1,x=0;char s=getchar(); while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();} while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();} return x*f; } struct EDGE{ int x,y,z,flagg; }w[M]; struct edgee{ int to,nextt,val; }e[M]; int tot=0,m,n,minn=INF; LL ans=0; int f[N][22],max1[N][22],g[N][22],fa[N],head[N],dep[N]; bool cmp(const EDGE &a,const EDGE &b) { return a.z<b.z; } int getfa(int x) { if(fa[x]==x) return x; return fa[x]=getfa(fa[x]); } void add(int a,int b,int v) { tot++; e[tot].to=b; e[tot].nextt=head[a]; e[tot].val=v; head[a]=tot; } void kruscal() { int q=1; sort(w+1,w+m+1,cmp); for(int i=1;i<=n;++i) fa[i]=i; for(int i=1;i<=m;++i) { int s1=getfa(w[i].x); int s2=getfa(w[i].y); if(s1!=s2) { ans+=w[i].z;w[i].flagg=1; q++; fa[s1]=s2; add(w[i].x,w[i].y,w[i].z); add(w[i].y,w[i].x,w[i].z); } if(q==n) break; } } void dfs(int x) { for(int i=head[x];i;i=e[i].nextt) { int v=e[i].to; if(v==f[x][0]) continue; f[v][0]=x; max1[v][0]=e[i].val; dep[v]=dep[x]+1; for(int j=1;j<=20;++j) { if(dep[v]<(1<<j))break;//注意：如果深度小于向上走的步数就可以break掉了 f[v][j]=f[f[v][j-1]][j-1];//f是向上走到达的点 max1[v][j]=max(max1[v][j-1],max1[f[v][j-1]][j-1]);//max1是最大边 if(max1[v][j-1]==max1[f[v][j-1]][j-1]) g[v][j]=max(g[v][j-1],g[f[v][j-1]][j-1]);//g是次大边 else { g[v][j]=min(max1[v][j-1],max1[f[v][j-1]][j-1]); g[v][j]=max(g[v][j],g[f[v][j-1]][j-1]); g[v][j]=max(g[v][j-1],g[v][j]); } } dfs(v); } } int LCA(int u,int x) { if(dep[u]<dep[x])swap(u,x); for(int i=20;i>=0;--i)if(dep[f[u][i]]>=dep[x])u=f[u][i]; if(x==u) return x; for(int i=20;i>=0;--i)if(f[x][i]!=f[u][i])x=f[x][i],u=f[u][i]; return f[x][0]; } void change(int x,int lca,int val) { int maxx1=0,maxx2=0; int d=dep[x]-dep[lca]; for(int i=0;i<=20;++i) { if(d<(1<<i))break; if(d&(1<<i)) { if(max1[x][i]>maxx1) { maxx2=max(maxx1,g[x][i]); maxx1=max1[x][i]; } x=f[x][i]; } } if(val!=maxx1) minn=min(minn,val-maxx1); else minn=min(minn,val-maxx2); } void work() { for(int i=1;i<=m;++i) { if(!w[i].flagg) { int s1=w[i].x,s2=w[i].y; int lca=LCA(s1,s2); change(s1,lca,w[i].z);change(s2,lca,w[i].z); } } } int main() { n=read();m=read(); for(int i=1;i<=m;++i) { w[i].x=read();w[i].y=read();w[i].z=read(); } kruscal(); // printf(">>%d\n",ans); dfs(1); work(); printf("%lld\n",ans+minn); } /* 5 7 1 3 1 1 4 10 3 4 2 3 2 3 2 4 7 1 5 1 3 5 19 */
写了好久终于写完了（撒花~✿✿ヽ(°▽°)ノ✿）
