弧度和角度之间的关系
前沿: 最近一直在可java,在用三角函数(其实,js里面也有),弧度和角度一些东西忘记了,小学没有学好。今天特地翻阅了一些资料,整理了一下三角函数弧度和角度之间的关系
<一>角的两种单位
1. “ 弧度”和“度”是度量角大小的两种不同的单位。就像“米”和“市尺”是度量长度大小的两种不同的单位一样。
2. 在flash里规定:在旋转角度(rotation)里的角,以“度”为单位;而在三角函数里的角要以“弧度”为单位。这个规定是我们首先要记住的!!!例如:rotation2--是旋转“2度”;sin(π/2)--是大小为“π/2弧度”的角的正弦。
<二>两种定义
1. 度的定义
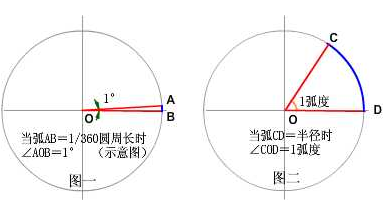
两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆周长的360分之一时,两条射线的夹角的大小为1度。(如图1)
2. 弧度的定义
弧度又是怎样定义的呢? 弧度的定义是:两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆的半径时,两条射线的夹角大小为1弧度。(如图2)
区别:
1. 比较一下,度和弧度的这两个定义非常相似。它们的区别,仅在于角所对的弧长大小不同。度的是等于圆周长的360分之一,而弧度的是等于半径。
简单的说,弧度的定义是,当角所对的弧长等于半径时,角的大小为1弧度。
2. 角所对的弧长是半径的几倍,那么角的大小就是几弧度。
角(弧度) = 弧长/半径
圆的周长是半径的2π倍,所以一个周角(360度)是2π弧度。
<三> 两者之间的换算关系
1. 据上所述,一个平角是 π 弧度。 即 180度=π弧度 ;
由此可知:
1度=π/180 弧度 ( ≈0.017453弧度 )
因此,得到 把度化成弧度的公式:
弧度=度×π/180
例如:
90°=90×π/180 =π/2 弧度
60°=60×π/180 =π/3 弧度
45°=45×π/180 =π/4 弧度
30°=30×π/180 =π/6 弧度
120°=120×π/180 =2π/3 弧度
2. 反过来,弧度化成度怎么算?
因为 π弧度=180°
所以 1弧度=180°/π (≈57.3°)
因此,可得到 把弧度化成度的公式:
度=弧度×180°/π
例如:
4π/3 弧度=4π/3 ×180°/π =240°.
<四--总结>
也许有些朋友会说,究竟是乘以“π/180 ”,还是“180°/π”很容易搞错。其实你只要记住:π是π弧度,180是180度。我要化成什么单位,就要把有这个单位的放在分子上。也就是说我要化成弧度,就要把π弧度放在分子上--乘以π/180 。另外,1度比1弧度要小得多,大约只有0.017453弧度(π/180≈0.017453)。所以把度化成弧度后,数字肯定要变小,那么化弧度时一定是乘以π/180 了。能够这样想一想,就不会搞错了。
在AS代码里把“π”写成“PI”。又因为“π”、“sin”都是“数学函数”,按规定要在前面加上“Math.”(Math是英语中“数学”Mathematics的缩写),加上后写成“Math.PI”、“Math.sin”。
所以 sin30°就得写成 Math.sin(30*Math.PI/180)。其中小括弧内的部分是把30°化为弧度,即30×π/180 。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号