算法第四章作业

1、你对贪心算法的理解

　　当一个问题具有最优子结构时，可用动态规划法求解，但有时会有更简单有效的方法——贪心算法。顾名思义，贪心算法总是在某种意义上的局部最优选择。当然，我们希望贪心算法得到的最终结果也是整体的最优。贪心算法的基本思路是从问题的某一个初始解出发一步一步地进行，根据某个优化测度，每一步都要确保能获得局部最优解。每一步只考虑一个数据，他的选取应该满足局部优化的条件。若下一个数据和部分最优解连在一起不再是可行解时，就不把该数据添加到部分解中，直到把所有数据枚举完，或者不能再添加算法停止。

2、请说明汽车加油问题的贪心选择性质

问题描述：

 

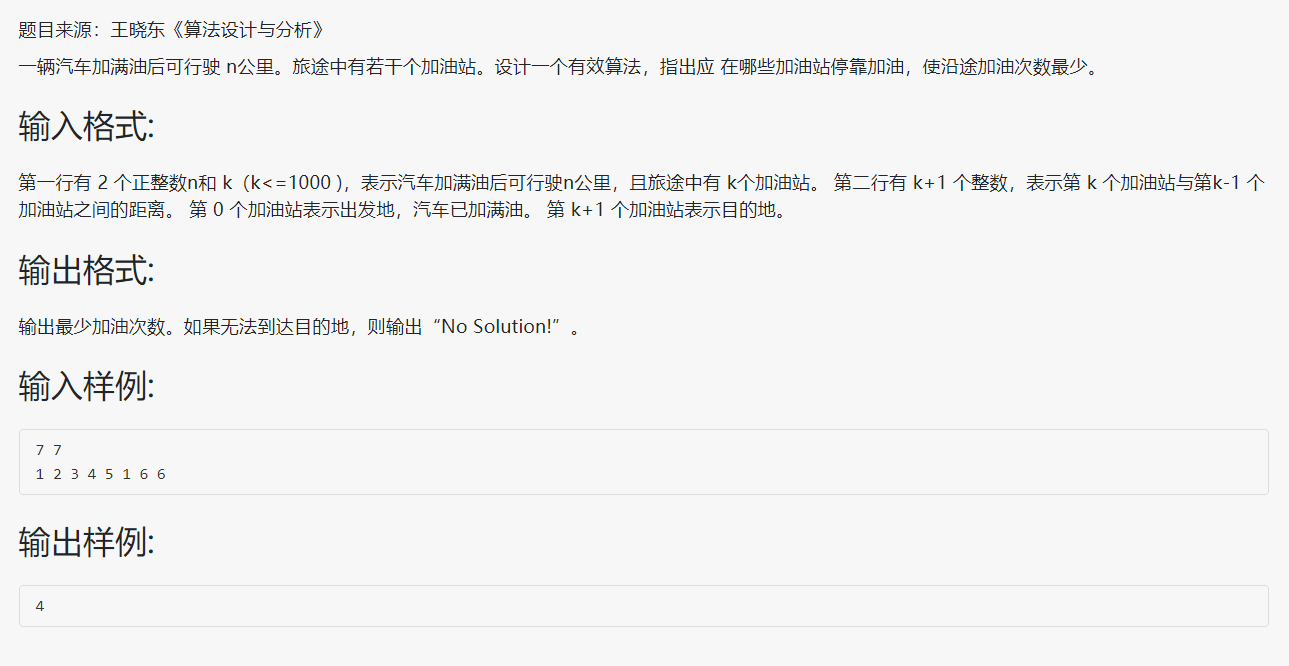
AC代码：

//输入格式:
//第一行有 2 个正整数n和 k（k<=1000 )，表示汽车加满油后可行驶n公里，且旅途中有 k个加油站。 第二行有 k+1 个整数，表示第 k 个加油站与第k-1 个加油站之间的距离。 第 0 个加油站表示出发地，汽车已加满油。 第 k+1 个加油站表示目的地。
//
//输出格式:
//输出最少加油次数。如果无法到达目的地，则输出“No Solution!”。
//
//输入样例:
//7 7
//1 2 3 4 5 1 6 6 
//输出样例:
//4
#include <iostream>
using namespace std;
int main(){
    int n, k;
    int a[1005];
    int count = 0;
    cin>>n>>k;
    int rest = n;
    for(int i = 0; i < k + 1; i++){
        cin>>a[k - i];
    }
    for(int i = 0; i < k + 1; i++){
        if(a[i] <= rest){
            rest = rest-a[i];
        }
        else{
            if(a[i] > n){
                cout<<"No Solution!"<<endl;
                return 0;
            }
            else{
                rest = n - a[i];
                count++;
            }
        }
    }
    cout<<count<<endl;
} 

 

　　汽车加油问题的贪心选择性质实质上是找到汽车满油量时可以行驶的最大路程范围内的最后一个加油站，加油后则继续用此方法前进，并且需要检查每一小段路程是否超过汽车满油量时的最大支撑路程，如果太贪心不加油，导致下一站到不了，则输出"No Solution！"。

3、请说明在本章学习过程中遇到的问题及结对编程的情况

　　本章学习其实和动态规划蛮相似的，首先要想清楚贪心策略，这点很重要，如果不是最佳贪心策略，那么最后做出来的也是错的；其次就是敲代码的基本功了，和泽伟小哥哥的结对编程让本菜鸡成功的AC了一题，希望下次继续努力！