算法第四章上机实践报告

1、实践题目：最优合并问题

2、问题描述：

 

 

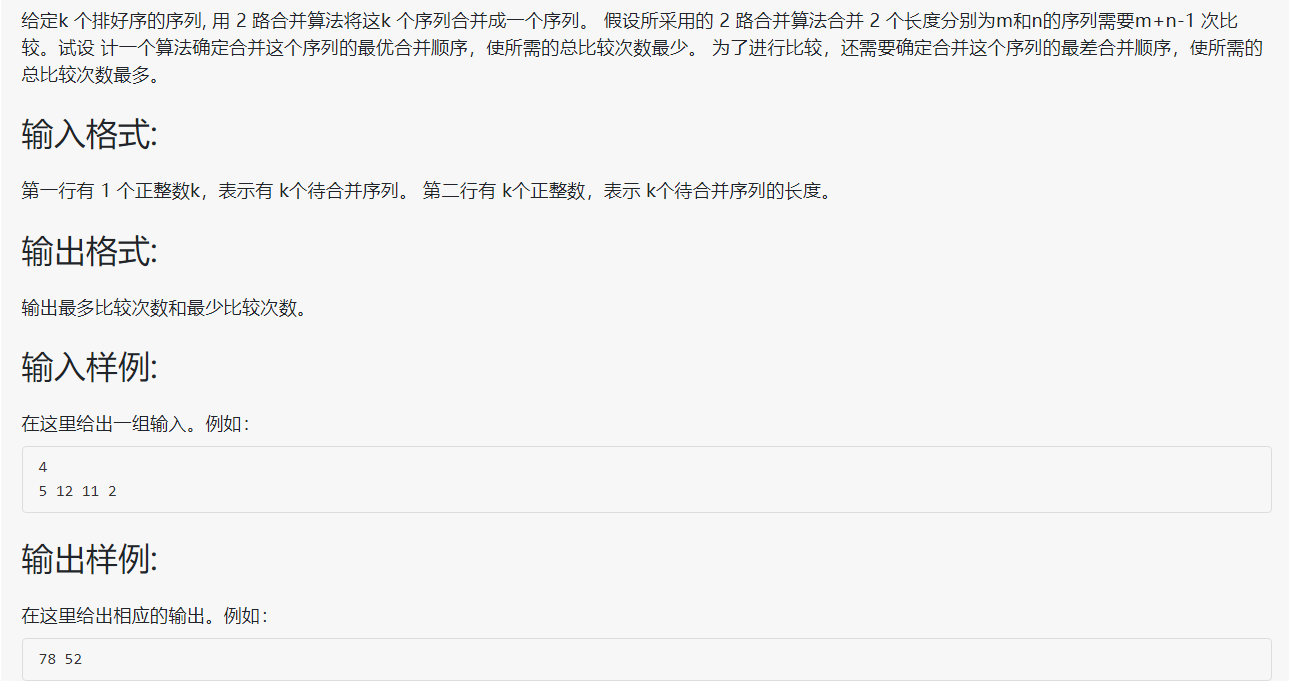
 3、算法描述（说明你的贪心策略，并且参考会场安排问题，利用反证法证明贪心选择和最优子结构性质）：

贪心策略：最多比较次数：选择最大和第二大的数，依次递减；最少比较次数：选择最小和第二小的数；

反证法证明：

　　设序列集合E=｛1，2，...，n｝以按长度大小的非减顺序排列，序列1具有最短的长度。

　　1、首先必有最优解包含序列1

　　不然设AE是最优解且A中最短的序列是k。若k=1，则最优解包含序列1，若k>1，则序列1必比序列k短，可以代替序列k，令B=A-{K}+{1},则B也是一个最优解。

　　2、进一步，若A是原问题的包含序列1的最优解，则A'=A-{1}是活动集合E'=E-{1}的最优解

　　不然设B'是E'的解且|B'|>|A'|,则B'∪{1}是E的解且|B'|+1>|A|,此与A是最优解矛盾。

#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
    int k;
    cin>>k;
    int* a = new int[k];
    int* b = new int[k];
    
    for(int i = 0; i < k; i++)
    {
        cin>>a[i];
        b[i] = a[i];
    }

    sort(a, a + k);

    int ssum = 0;
    int smark = 0;
    while(smark < k - 1)
    {
        ssum = ssum + a[smark] + a[smark+1] - 1;
        a[smark] = a[smark] + a[smark+1];
        a[smark+1] = 0;
        smark++;
        sort(a, a + k);
    }
    sort(b, b + k);
    int bsum = 0;
    //int bmark = 0;
    for(int i = 1; i <= k - 1; i++)
    {
        bsum = bsum + b[k - 1] + b[k - 2] - 1;
        b[k - 1] = b[k - 1] + b[k - 2];
        b[k - 2] = 0;
       // bmark++;
        sort(b, b + k);
    }
    cout<<bsum<<" ";
    cout<<ssum;
    return 0;
}

4、算法时间及空间复杂度分析（要有分析过程）

时间复杂度：排序：O(nlogn)，合并(n-1)(2*O(1)+O(n))=O(n^2)；

空间复杂度：O(n^2）；

5、心得体会（对本次实践收获及疑惑进行总结）:

与上一章的动态规划来说，其实有些相似，动态规划只要找出动态规划公式，其余问题不大，贪心算法也是如此，只需要弄清楚贪心策略，其余也很容易，对于此次的第二题，我们上机时是没有头绪的，我们想到了将该数%10分离出各个数字存入数组，但由于过于麻烦，所以没能做出来，经过老师的提醒，把他设成一个字符串，问题便简单许多，总的来说，是我们见识的题目还不够多，有些想当然就钻进死胡同里，这时候不如跳出陷阱，重新思考会得到更好的算法。