算法第三章上机实践报告

1、实践题目：7-1 数字三角形

2、问题描述：

 

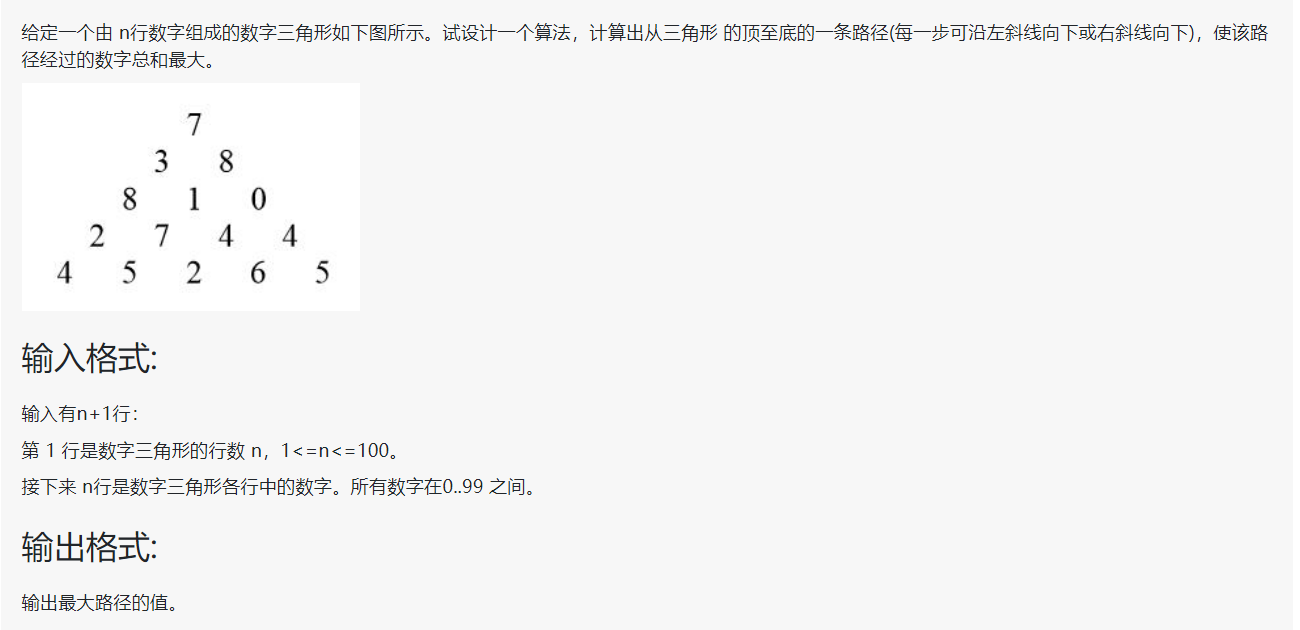
 3、算法描述

#include <iostream>
using namespace std;
int b[10005][10005];
int numberTriangle(int a[1005][1005], int n){
 
 for(int i = n - 1; i >= 0; i--){
  for(int j = i; j >= 0; j--){
   b[i][j] = ((b[i + 1][j] > b[i + 1][j + 1]) ? b[i + 1][j] : b[i + 1][j + 1]) + a[i][j];
  }
 }
 return b[0][0];
}
int main(){
 int n, i ,j;
 int a[1005][1005];
 cin >> n;
 for(i = 0; i < n; i++){
  for(j = 0; j <= i; j++){
   cin >> a[i][j];
  }
 }
 cout << numberTriangle(a, n) << endl;

 return 0;
} 

4、算法时间及空间复杂度分析（要有分析过程）

时间复杂度:由于每个数组单元的计算耗费O（1）时间，因此算法numbertriangle耗时O（n²），而main函数中时间复杂度为O(n²)，所以总的时间复杂度为O（2n²）;

空间复杂度:由于算法内有一个嵌套循环，因此算法numbertriangle空间复杂度O（n²），而main函数中亦如此，空间复杂度为O(n²)，所以总的空间复杂度为O（2n²）;

5、心得体会（对本次实践收获及疑惑进行总结）

结对编程是真的好，有些思路卡住了，小伙伴就能为你排忧解难，在编程中，填表的过程中我一直想不明白要求的是哪个三角形，我的同伴画了个图一下子就清晰明了了，我也发现动态规划最重要的是推出动态规划的公式，希望下次能做出更难的题！