算法第二章上机实践报告

1、实践题目：7-1 二分查找（此题与詹泽伟同学一同完成）

2、问题描述：

 

 

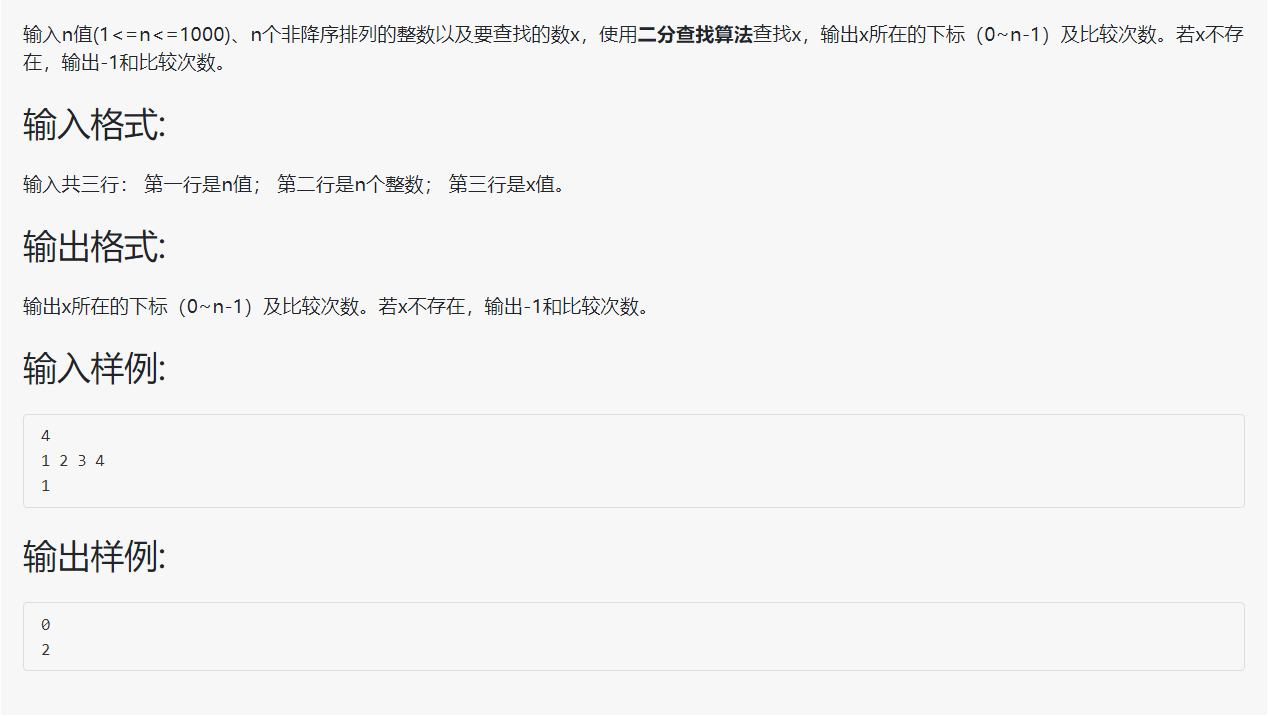
 3、算法描述：

　　第一种方法（循环）：

#include<iostream>
using namespace std;
int BS(int a[],int x, int n){
    int l = 0;
    int r = n - 1;
    int count = 0;
    while(l <= r){
    count ++;
    int m =(l + r) / 2;
    if(x == a[m]) {
        cout << m <<endl << count;
        return m;
    }
    if(x > a[m]){
        l = m+1;
        }
    else {
        r = m-1;
    }
    }

    cout << "-1" <<endl << count;
    return -1;
}
int main(){
    int a[1005];
    int n, x;
    cin >> n;
    for(int i = 0; i < n; i++){
        cin >> a[i];
    }
    cin >> x;
    BS(a, x, n) ; 
    return 0;
}

　　第二种方法（递归）：

#include <iostream>
using namespace std;
int BS(int a[], int x, int l, int r, int &count){
    count ++;
    if(l == r){
        if(x == a[l])
            return l;
        else
            return -1;
    while(l < r){
        int m = (l + r) / 2;
        if(x == a[m])
            return m;
        if(x < a[m]) 
            return BS(a, x, l, m-1, count);
        if(x > a[m])
            return BS(a, x, m+1, r, count);
    }
    }
}
int main()
{
    int a[1005];
    int n, x ,count = 0;
    cin>>n;
    for(int i = 0; i < n; i++){
        cin>>a[i];
    }
    cin>>x;
    cout<<BS(a, x, 0, n-1, count) << endl ;
    cout<<count;
    return 0;
}

　　其中count用来判断循环次数，此题比较基础。

4、算法时间及空间复杂度分析

　　第一种方法(循环): 通过代码分析，BS函数当中假设最坏情况下，循环X次之后找到，则：2^x=n; x=logn(算法中如果没写，log默认底数为2)，循环的基本次数是log2 N，所以时间复杂度是O(logN)，而main函数里面有一个构建数组的for循环，共经过了n次循环，因此时间复杂度为O（n），所以函数的空间复杂度为O(n)。（时间复杂度）

　　main函数里面定义了一个a[n]因此需要一个长度为n的空间，而常数则忽略不计，因此空间复杂度为O（n）。(空间复杂度)

　　第二种方法(递归): 通过代码分析，BS函数当中假设最坏情况下，循环X次之后找到，则：2^x=n; x=logn(算法中如果没写，log默认底数为2)，递归的次数和深度都是log2 N,每次所需要的辅助空间都是常数级别的。（时间复杂度）

　　BS函数里的空间复杂度为O(log2 N)，而main函数里面定义了一个a[n]因此需要一个长度为n的空间，所以函数空间复杂度为O（n + log2 N）。（空间复杂度）

5、实践收获

　　1）遇到的问题：

　　在写第一种方法的时候，一开始在BS函数中没有return m，还好我的小伙伴及时提醒了我（一直没意识到QAQ），第二种方法用了递归，琢磨了半个小时也没有琢磨出来，最后请教了老师，老师指出了问题的关键。开始时cout<<BS(a, x, 0, n-1, count) << endl << count ;这样的count只会是1，正确的做法应该是cout<<BS(a, x, 0, n-1, count) << endl ;　　cout<<count;

　　2）心得体会：感觉有个小伙伴真的比自己码要好（起码有个人陪自己一起脑壳疼嘿嘿...